如何做好一份【数学类】技术文档

前言

我这里主要是数学方向，毕竟钻研了这么多年都是这个方向的内容，必须在此次活动中分享一番。

评分说明

评审总分（100%）= 内容质量评分（60%）+博文综合数据【点赞+收藏数+评论数】（30%，上限30分）+博文阅读量（10%，上限10分）；

数学类文章难点说明

数学文章其实看的人基本都是圈内的，但是也会有一些素人来看，圈内看的文章也都是一些大佬相互学习，小算法什么分享素人们看的会多一些，毕竟难度一上，很多人看着就都是天书了，简单举个例子。

grid = [
    [1, 1, 0, 0, 0],  # 左上角岛屿
    [0, 1, 0, 1, 1],  # 中间障碍物和右侧小岛
    [0, 0, 0, 1, 0],  # 右侧垂直通道
    [1, 1, 1, 0, 0],  # 下方大面积岛屿
    [1, 0, 0, 0, 1]   # 分离的角落区域
]

这相当于一个面板，那么接下来我想把1和0调换。

# 5x5 二维数组示例 (1=可通行区域，0=障碍物)
grid = [
    [1, 1, 0, 0, 0],  # 左上角岛屿
    [0, 1, 0, 1, 1],  # 中间障碍物和右侧小岛
    [0, 0, 0, 1, 0],  # 右侧垂直通道
    [1, 1, 1, 0, 0],  # 下方大面积岛屿
    [1, 0, 0, 0, 1]   # 分离的角落区域
]
# 1和0进行调换 
grid = [[1 - value for value in row] for row in grid]
# 打印二维数组
for row in grid:
    print(row)

核心代码：

1 - value for value in row

这里的1就很好玩：

1-1(原)=0(新)

1-0(原)=1(新)

这样1和0就进行了交互，很好玩的东西。

传统变换

grid = [[1 if value == 0 else 0 for value in row] for row in grid]

这一下就少了很多灵魂，还得多一对if（）else来做判断。

目标人群

从上方的一个小示例上就能看出来，我们搞数学算法的人们所写的文章肯定目标性是很强的，我们针对的是数学算法方向的特定人群，那么对应我们所编写的文章也一定要符合我们的人群学习方式。

数学学习的一般流程

数学学习是一个从基础认知到综合应用的渐进过程，通常包含 知识理解、技能训练、应用实践、总结反思 四个核心环节。

知识理解：构建数学认知基础

理解数学概念、定理、公式的本质，明确其含义和适用条件。

感知与观察、概念抽象与概括、逻辑推导与证明、关联与整合。

技能训练：掌握数学操作能力

通过练习熟练掌握计算、推理、绘图等基本技能，形成自动化反应。

针对性练习、强化运算能力、逻辑推理训练、工具与技术应用。

应用实践：解决实际问题与数学问题

运用数学知识解决生活中的实际问题或复杂的数学问题，培养建模能力。

问题分析与建模、求解与验证、综合问题解决。

总结反思：深化理解与优化学习

通过总结规律和反思错误，提升学习效率，形成个性化的学习方法。

知识总结与结构化、错题分析与改进、学习策略调整。

梳理数学学习一般流程——文档化

阶段	核心目标	关键动作	成果 / 输出	工具 / 方法
1. 基础认知	理解概念、定理、公式的本质	观察实例 / 符号 抽象概括概念 推导证明 知识关联	形成知识笔记、概念思维导图	实例分析法、逻辑推导法
2. 技能训练	熟练掌握计算、推理等技能	分类型练习 强化运算速度 逻辑推理训练 工具辅助	错题集、解题步骤总结表	刻意练习法、错题分析法
3. 应用实践	解决实际问题与综合题	问题建模 多方法求解 跨知识点整合 结果验证	数学模型、问题解决方案报告	建模法、一题多解法
4. 总结迭代	优化知识体系与学习策略	制作知识框架图 分析错题原因 调整学习方法 定期复盘	知识体系脑图、学习策略优化清单	思维导图工具、费曼技巧

脑图梳理：

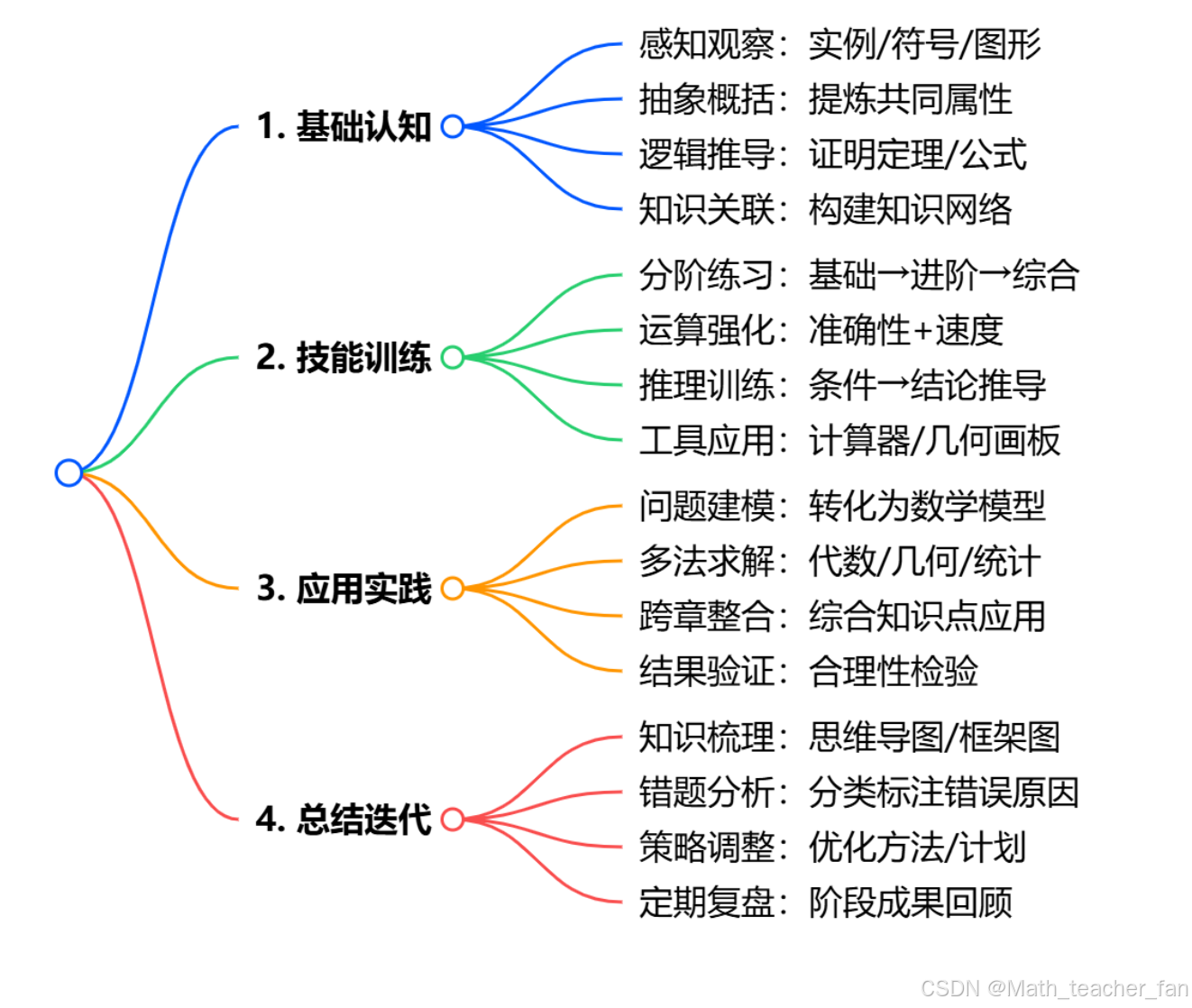
对应学习工具

场景	工具 / 资源	用途
知识梳理	Xmind、幕布	制作思维导图
错题管理	橙果错题本、Excel 表格	分类整理错题，统计薄弱环节
几何绘图	几何画板、Desmos	辅助理解图形性质，动态演示变化
公式推导练习	白板 / 草稿纸	手写推导过程，强化逻辑记忆
综合题训练	中考 / 高考真题分类汇编	接触典型题，总结命题规律

文档格式整理

根据以上的数学学习一般流程分析，我们可以得到想要给数学类文章读者一篇好的可以深入阅读学习的文章需要提供以下内容：

文章创作阶段	核心任务	内容要点	输出形式
1. 规划与定位	明确文章目标与受众需求	确定文章类型（知识科普 / 解题技巧 / 应用案例） 分析读者知识水平（初学者 / 进阶者 / 专业人士） 提炼核心主题（如 “导数在优化问题中的应用”）	主题大纲、受众画像文档
2. 基础认知构建	拆解核心概念，降低理解门槛	生活化类比（用 “快递配送路线” 解释最短路径算法） 公式推导分步图解（动态演示几何定理证明过程） 关联已有知识（对比新旧知识点异同）	图文解析、动态演示视频
3. 技能训练设计	提供可操作的解题与应用指导	阶梯式习题集（基础题→综合题→拓展题） 易错点标注与避坑指南（用红框标出高频错误步骤） 解题策略总结（归纳 10 种常见函数题型解法）	习题表、策略清单
4. 应用实践深化	展示知识在实际场景中的应用	真实案例拆解（用线性规划解决仓储布局问题） 一题多解对比（代数法 vs 几何法解题效率分析） 跨学科案例（数学在人工智能算法中的应用）	案例报告、对比分析图表
5. 总结与互动	强化知识记忆，促进读者反馈	章节思维导图（含核心公式与逻辑关系） 个性化学习建议（针对不同学习阶段的提升方案） 互动环节（设置开放性问题或在线小测试）	思维导图、互动问答模块
6. 优化与发布	完善内容质量，扩大传播效果	校对逻辑漏洞与计算错误 添加关键词与元数据优化搜索 适配多平台格式（网页版 / 移动端 / PDF）