可持久化线段树学习笔记

可持久化线段树学习笔记

可持久化线段树

假如有一颗线段树如下（黑色部分）：

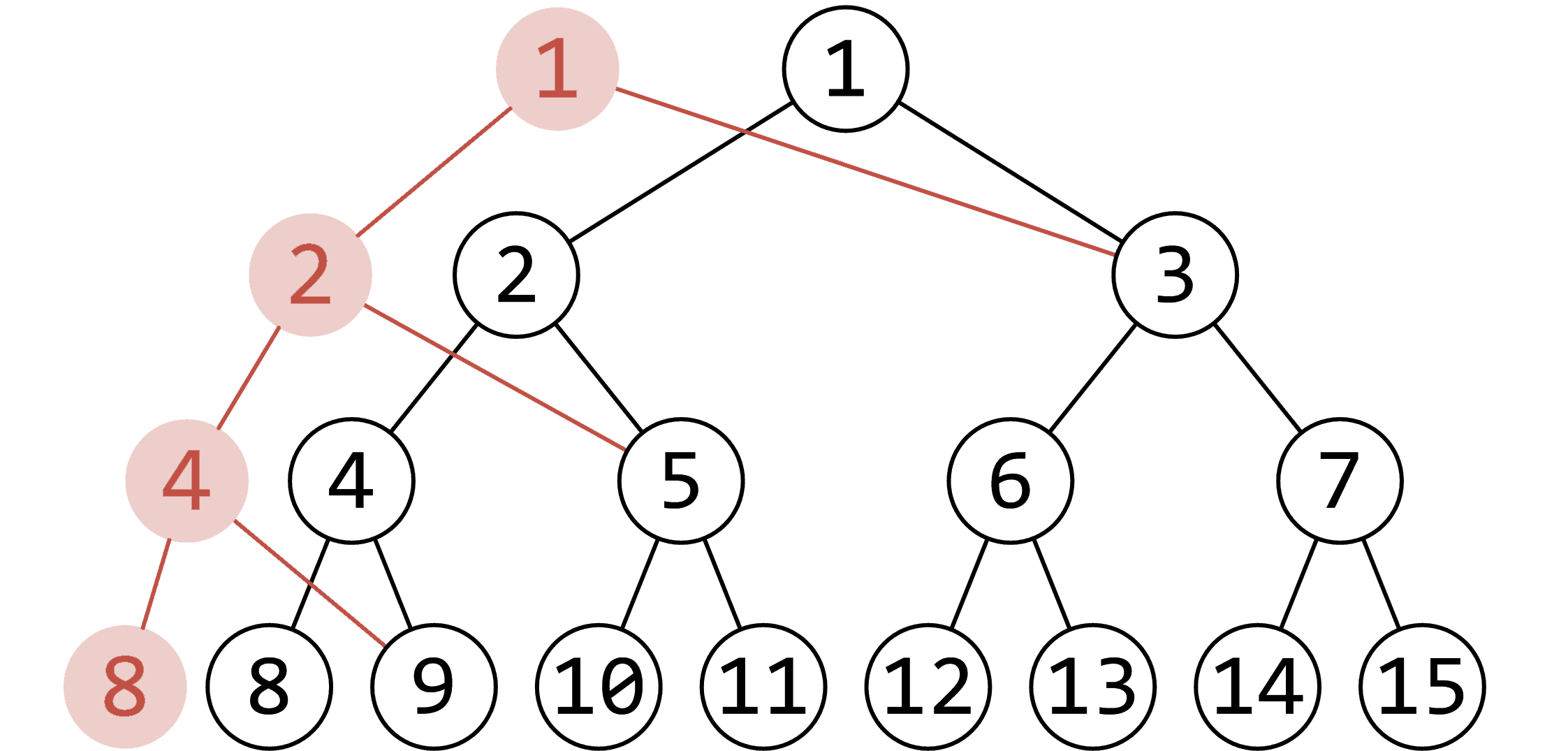
现在要修改权值为 $1$ 的点（在线段树中对应编号为 $8$），那么从根到对应点的一条长为 ${\log }_{2}n$ 的链（红色部分）就会被插入到原来的线段树。

现在考虑怎么在历史版本上修改。

其实我们发现，历史版本对现在版本的印象仅限于两点的 LCA 到根的那一条链。

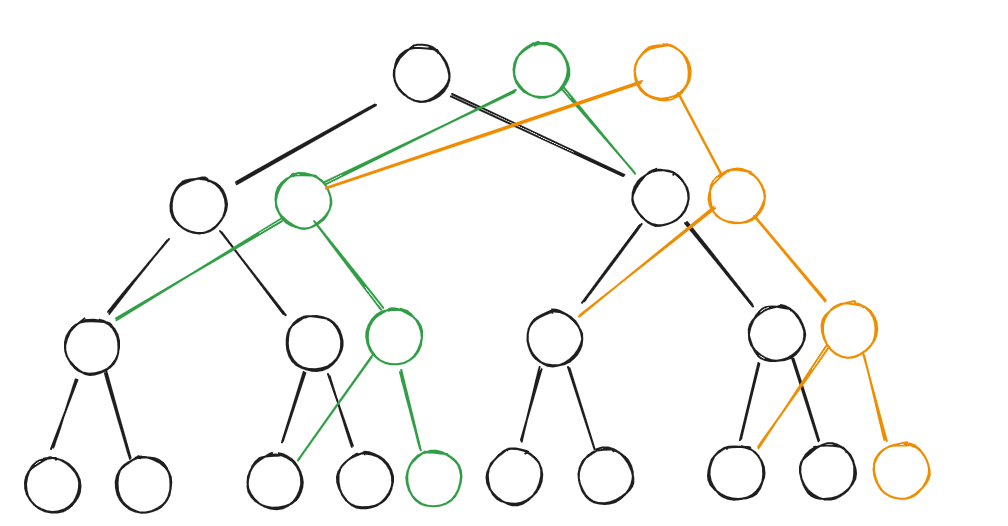
在上图中，绿色点是黑色点的修改版本，橙色点是绿色点的修改版本，但是修改的节点不在绿色链上。

但实际上这其实无关紧要，因为根不一样，所以根的子树可以代表一个版本。实际上我们可以这样画图。

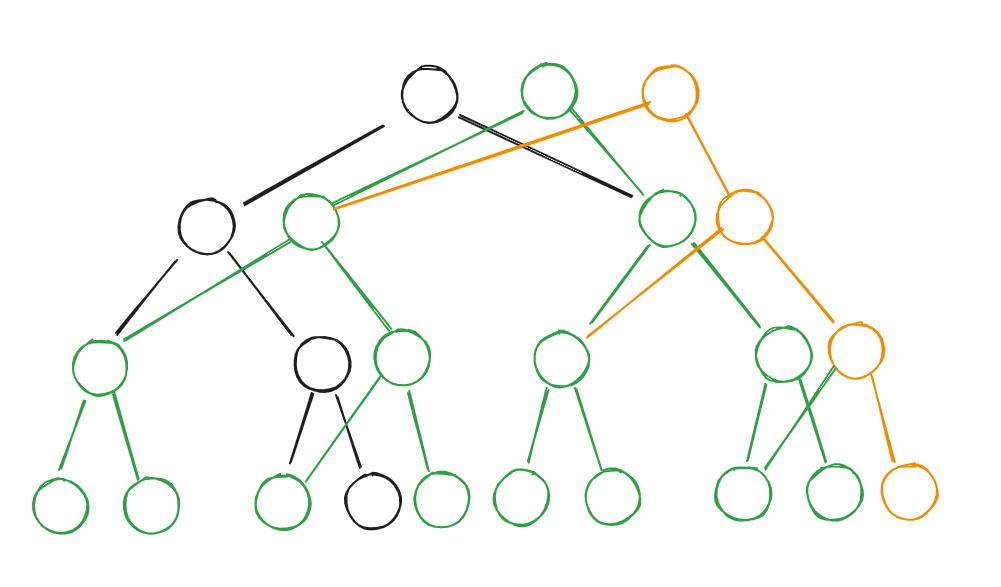
所以每次做链上的修改的时候，只需要把链上的点复制一份，再根据回溯过来的结果指定左右儿子即可。

总结一下，就是动态开点，但是根有版本之间的区分。

例题 P3919 【模板】可持久化线段树 1（可持久化数组）

#include <bits/stdc++.h>
using namespace std;
using ll = long long;
const int N = 1e6;
int n, m;
int rt[N + 5], a[N + 5];// 表示版本 i 的根节点编号 rt[i] 
int val[(N << 5) + 5], ls[(N << 5) + 5], rs[(N << 5) + 5];// 表示 i 号节点的权值 
int cnt;

int new_node(int num){
	cnt++;
	ls[cnt] = ls[num], rs[cnt] = rs[num], val[cnt] = val[num];
	return cnt;
}

int build(int num, int l, int r){
	num = ++cnt;
	if(l == r){
		val[num] = a[l];
		return num;
	}
	int mid = (l + r) >> 1;
	ls[num] = build(ls[num], l, mid);
	rs[num] = build(rs[num], mid + 1, r);
	return num;
}

int upd(int num, int l, int r, int x, int v){
	num = new_node(num);
	if(l == r)	val[num] = v;
	else{
		int mid = (l + r) >> 1;
		if(x <= mid)
			ls[num] = upd(ls[num], l, mid, x, v);
		else
			rs[num] = upd(rs[num], mid +1, r, x, v);
	}
	return num;
}

int qry(int num, int l, int r, int x){
	if(l == r)	return val[num];
	else{
		int mid = (l + r) >> 1;
		if(x <= mid)	return qry(ls[num], l, mid, x);
		else	return qry(rs[num], mid + 1, r, x);
	}
}

signed main(){
	ios::sync_with_stdio(false);
	cin.tie(nullptr);
	cin>>n>>m;
	for(int i = 1;i <= n;i++){
		cin>>a[i]; 
	}
	rt[0] = build(0, 1, n);
	for(int i = 1;i <= m;i++){
		int rot, op, p;
		cin>>rot>>op>>p;
		if(op == 1){
			int c;	cin>>c;
			rt[i] = upd(rot[rt], 1, n, p, c);
		}
		else{
			cout<<qry(rt[rot], 1, n, p)<<'\n';
			rt[i] = rt[rot];
		}
	}
	return 0;
}

主席树

主席树就是可持久化权值线段树。

例题 P3834 【模板】可持久化线段树 2

给定 $n$ 个整数构成的序列 $a$，查询 $[l,r]$ 中第 $k$ 小值。

维护一棵可持久化权值线段树，父节点 $[l,r]$ 表示有多少个数 $x\in [l,r]$。

假如从 $a_1$ 遍历到 $a_n$，当遍历到 $a_i$ 时，将线段树中 $val[a_i]$ 增加 $1$ 并备份到新的版本 $i$。那么这个版本 $i$ 表示的是 $1\sim i$ 的权值线段树。

假如我要找 $[1,i]$ 中第 $k$ 大的数，那么我可以在第 $i$ 个版本进行线段树上二分，即，当节点 $u$ 的左儿子大小（表示区间内数的数量）大于等于 $k$ 时往左走，否则往右走。

现在我需要找到两个版本的权值线段树，能代表 $[l,r]$。容易发现，如果我们把 $r$ 版本的权值线段树减去 $l-1$ 版本的权值线段树（所有节点都相减，相当于统计了 $[l,r]$ 的桶），那么差就能代表 $[l,r]$ 的权值线段树了。

而可持久化权值线段树就是主席树。

#include <bits/stdc++.h>
#define pii pair<int, int>
#define pb push_back
using namespace std;
using ll = long long;
const int N = 2e5 + 5;
int n, m, len, cnt;
int sum[N << 5], ls[N << 5], rs[N << 5], rt[N]; 
int a[N], b[N];// Ô­Êý×éºÍÀëÉ¢Ö®ºóµÄÊý×é 

int new_node(int num){
	++cnt;
	sum[cnt] = sum[num] + 1, ls[cnt] = ls[num], rs[cnt] = rs[num];
	return cnt;
}

void build(int &num, int l, int r){
	num = ++cnt;
	if(l == r)	return;
	int mid = (l + r) >> 1;
	build(ls[num], l, mid);
	build(rs[num], mid + 1, r);
}

int upd(int num, int l, int r, int p){
	num = new_node(num);// ¸´Öƽڵã
	if(l == r)	return num;
	int mid = (l + r) >> 1;
	if(p <= mid)	ls[num] = upd(ls[num], l, mid, p);
	else	rs[num] = upd(rs[num], mid + 1, r, p);
	return num;
}

int qry(int fir, int sec, int l, int r, int k){
//	cout<<l<<" "<<r<<'\n';
//	cout<<sum[ls[sec]]<<" ls[sec], ls[fir] "<<sum[ls[fir]]<<'\n';
	if(l == r)	return l;
	int mid = (l + r) >> 1, x = sum[ls[sec]] - sum[ls[fir]];
	if(x >= k)	return qry(ls[fir], ls[sec], l, mid, k);// Íù×ó¶ù×Ó×ß 
	else	return qry(rs[fir], rs[sec], mid + 1, r, k - x);// ÍùÓÒ¶ù×Ó×ß 
}

signed main(){
	ios::sync_with_stdio(false);
	cin.tie(nullptr);
	cin>>n>>m;
	for(int i = 1;i <= n;i++){
		cin>>a[i];	b[i] = a[i];
	}
	sort(b + 1, b + n + 1);
	len = unique(b + 1, b + n + 1) - b - 1;
	build(rt[0], 1, len);// Ö÷ÒªÊÇ°Ñ ls, rs ´¦ÀíºÃ£¬ÀíÂÛÉÏÀ´½²¿ÉÒÔ O(n) ½â¾ö 
	for(int i = 1;i <= n;i++){
		int p = lower_bound(b + 1, b + len + 1, a[i]) - b;// ÀëÉ¢»¯ 
		rt[i] = upd(rt[i-1], 1, len, p); 
	}
	while(m--){
		int l, r, k;	cin>>l>>r>>k;
		cout<<b[qry(rt[l-1], rt[r], 1, len, k)]<<'\n';
	}
	return 0;
}