Leetcode将有序数组转换为二叉搜索树算法与分析

@Leetcode将有序数组转换为二叉搜索树

又是一个让笔者看到就如临大敌的题目，看了半天数据结构的书也没找到好的思路，经过高人点拨，知道了一个叫中序遍历必然有序的二叉搜索树的概念。请看题干：

将一个按照升序排列的有序数组，转换为一棵高度平衡二叉搜索树。
本题中，一个高度平衡二叉树是指一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1。
示例:

当你真正想明白，玩清楚这个题目和一些二叉树的经典性质时，这肯定算不上一个难题，甚至只能说是入门，可惜小白笔者连门都没入。。。七搞八搞左问右查才明白，写出了一份极不真实但能够通过的代码：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    TreeNode* toBST(vector<int>& nums,int first,int last){
        if(first>last)
            return NULL;
        int midPoint=(first+last)/2;
        TreeNode* fatherPoint=new TreeNode(nums[midPoint]);
        fatherPoint->left=toBST(nums,first,midPoint-1);
        fatherPoint->right=toBST(nums,midPoint+1,last);
        return fatherPoint;
    }
    
     TreeNode* sortedArrayToBST(vector<int>& nums) {
        return toBST(nums,0,nums.size()-1);
    }
};

虽然能够通过，但这份短短的代码的编写过程可谓艰辛，归根结底还是我太菜了。本题思路基本就是二分法和递归的结合，由于所给数组是是一个有序数组并且明显可以看出是一个中序遍历树的数组，我们可以通过不断进行二分来取得每一层的父结点。二分搜索的好处是可以不破坏原数组的排列同时找到大家最熟悉的结点输出方案。递归当然是必须的，但是注意递归终点一定一定一定要优先判断，并且要准确判断。本题的递归终点并不是输出NULL，而是在二分的头尾重合，不，应该是头超过尾的时候才能算结束。

下面的堆溢出的错误是小白笔者第x遍编写错误时，将nums.size()==0当成递归终点时出现的错误，后来发现原数组根本就没有改变，所以递归永远不会结束，自然就溢出了。

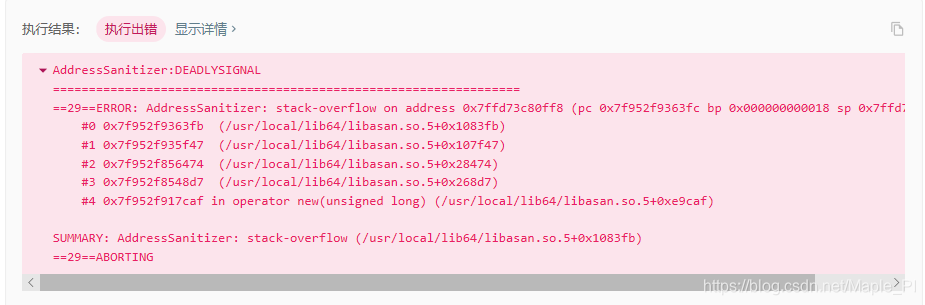
下面这个错误则是小白笔者在第x*x遍编写错误时，发现第二个案例都过不了，苦思冥想画树之后发现，first必须大于last而不能大于等于，希望前车之鉴能够帮助到大家。

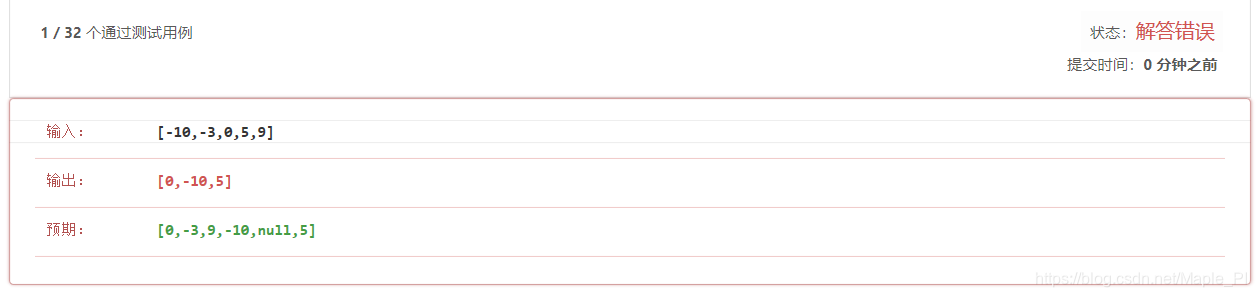
其他的一些代码的具体部分，相信每个coder都能对二分搜索方法有一些小了解。当然，即使编写结束了，笔者仍然对本题有一些不解之处，比如说就像案例之中说明这是其中一个可能的平衡树（平衡树是本题能够使用二分搜索法的关键），那么为什么不能得到其他答案呢？是不是与先判断左子树再判断右子树有关呢？于是笔者把右子树的判断调到左子树之前，代码依然可以通过，仔细一想其实调换左右顺序对答案并没有变化，那么其中奥妙到底在何处呢？

笔者找了百度百科二叉树的定义：二叉搜索树别名二叉排序树，它要么是一棵空树，要么具有如下性质：若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值； 若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值； 它的左、右子树也分别为二叉搜索树。

这说明答案的确可能出现不一样的情况，然而这种不同仅仅体现在画树的时候，比如说一棵三层的树，头结点A的左儿子B比头结点A小，这个左儿子结点B的右儿子结点C大于这个B结点而小于头结点A，那么这棵树也有另一个画法，那就是这个C作为A的直接左儿子，而B作为C的左儿子，这的确是两棵不同的树，然而我们在写中序遍历的时候就会发现，其实他们的中序遍历是相同的，对于本题的解答并无影响，当然就也和左右的优先判断并无干系啦。