2025超详细的数学建模入门速成指南

2025数学建模入门速成指南（自用版）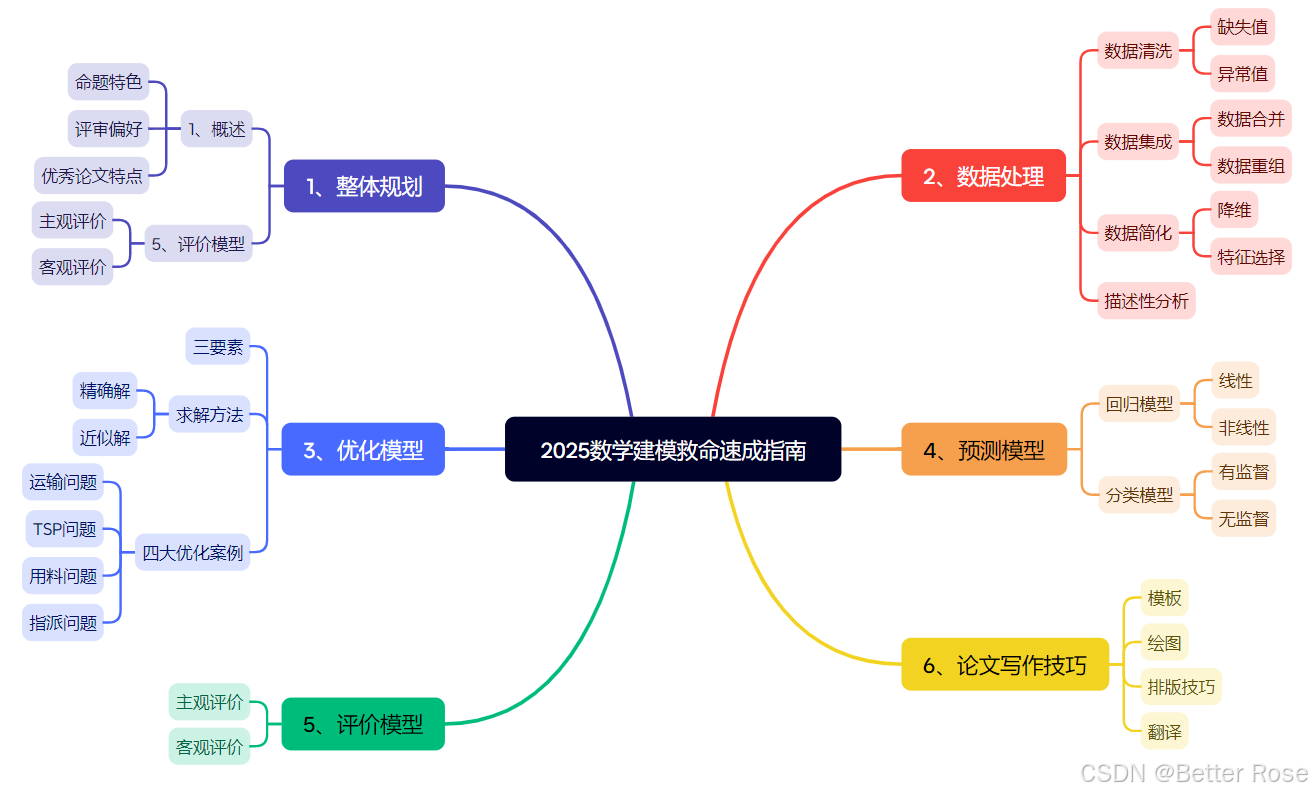

作为曾获国赛和华为杯双国一的选手，我认为数学建模入门关键在于掌握基础模型（优化、预测、评价）、数据处理思维（清洗、分析、可视化）以及有效的团队协作模式。这篇笔记结合我的自身经历，分享从【零基础到竞赛获奖】的准备思路。

01整体规划

1. 数模入门

数学建模竞赛考察我们解决实际问题的综合能力。在备赛初期首先建立以下认知基础：

（1）竞赛特点：

• 命题趋势：近年赛题倾向于跨学科综合性问题
• 评审标准：创新性(30%)、规范性(25%)、完整性(20%)、实用性(15%)、可读性(10%)
• 优秀论文共性：问题转化准确、模型适用性强、求解过程严谨、分析深入、表述规范

（2）备赛要点：

• 建立模型知识体系：掌握10-15个基础模型及其变体
• 收集历年赛题：分析近3年同级别竞赛的优秀论文
• 工具准备：Matlab/Python编程环境、SPSS/Excel分析工具、LaTeX/Word排版工具

2. 数据处理

高质量的数据处理是建模正确有效的前提，需要掌握以下方法：

（1）数据清洗：

• 异常值处理：3σ原则、箱线图法、聚类分析法
• 缺失值处理：删除法（<5%）、均值填充、回归填充、多重插补法
• 数据转换：标准化（Z-score）、归一化（Min-Max）、离散化

（2）数据集成：

• 数据重组
• 数据融合

（3）数据简化：

• 降维技术：PCA主成分分析（连续变量）、因子分析
• 特征选择

（4）描述性分析：

• 善于利用数据可视化

3. 优化模型

优化问题是数学建模的核心题型，需要掌握：

（1）模型构建三要素：

• 决策变量设置：明确变量类型（连续/离散）和维度
• 目标函数建立：单目标/多目标（权重法、约束法）
• 约束条件确定：等式约束与不等式约束的数学表达

（2）求解方法：

• 精确解法：单纯形法（线性）、分支定界法（整数）
• 近似算法：遗传算法（参数：种群规模50-200）、模拟退火（降温系数0.8-0.99）
• 工具实现：LINGO专用优化软件、MATLAB优化工具箱

（3）四大优化案例：

• 运输问题 \ TSP问题 \ 用料问题 \ 指派问题

4. 预测模型

预测类问题需建立方法选择框架：

（1）回归分析：

• 线性回归：OLS估计、显著性检验（p<0.05）
• 非线性回归：对数转换、多项式回归
• 诊断检验：残差分析、DW检验（自相关）、White检验（异方差）

（2）分类模型：

• 逻辑回归、决策树、SVM

（3）时间序列：

• ARIMA模型：（p,d,q）参数确定
• 预测评估：MAE、RMSE指标计算

5. 评价模型

（1）指标体系构建：

• AHP层次分析法、熵权法

（2）评价方法选择：

• TOPSIS、模糊综合评价、DEA数据包络分析

（3）结果验证：

• 敏感性分析：参数±10%变动测试
• 对比分析：与已有研究结果对照

6. 论文写作技巧

（1）标题：

• 要素：方法+对象+创新，如"基于熵权-TOPSIS的城市韧性评价"

（2）摘要撰写：

• 四段式结构：问题→方法→结果→结论
• 关键词：5-7个专业术语

（3）正文规范：

• 问题重述：改写题干（相似度<15%）
• 模型假设：5-8条合理简化
• 符号说明：三线表呈现

（4）可视化呈现：

• 图表规范：分辨率300dpi以上
• 公式排版：MathType编辑，右编号

第二部分：数模分工

1. 模型建立

• 数学基础：掌握微积分、线性代数、概率统计核心内容
• 模型识别：能根据问题描述匹配相应模型

典型工作流程：

1. 问题分析（2小时）：与队友讨论确定问题本质
2. 文献调研（3小时）：查阅类似问题的解决方法
3. 模型构建（5小时）：建立数学模型框架
4. 验证反馈（持续）：与代码实现得同学保持迭代沟通

2. 模型实现

• 编程能力：至少精通Python或MATLAB一种
• 算法实现：能将数学公式转化为可执行代码
• 调试技巧：掌握断点调试、日志输出等方法

工具链配置：

1. 基础工具：Anaconda+Jupyter环境
2. 数据处理：Pandas+NumPy组合
3. 可视化：Matplotlib/Seaborn图表库

3. 论文撰写

文档质量标准：

• 逻辑性：采用"问题导向"的行文结构
• 规范性：符合学术论文写作标准
• 美观性：图表排版协调统一

写作流程控制：

1. 框架搭建（4小时）：与团队确定大纲
2. 内容填充（8小时）：同步撰写各章节
3. 润色修改（4小时）：语言优化与格式调整
4. 终稿检查（2小时）：交叉验证结果一致性

第三部分：学习规划

基础阶段（40小时）

1. 模型入门（20小时）：

2. 数据处理（10小时）：Excel高级功能、Python基础处理

3. 论文规范（10小时）：摘要写作训练、图表制作练习

提高阶段（60小时）

1. 模型进阶（30学时）：时间序列预测、非线性优化、模糊综合评价
2. 编程强化（20学时）：MATLAB优化工具箱、Python机器学习库
3. 模拟实战（10学时）：完成2套往届赛题

冲刺阶段（80-100小时）

1. 专题突破（40小时）：针对薄弱环节强化、创新方法研究
2. 全真模拟（40小时）：3次72小时模拟

备赛时间轴

赛前3个月：

• 每周团队讨论会（2小时）
• 个人专项训练（10小时/周）

赛前1个月：

• 周末模拟赛（每月2次）
• 专家指导会（邀请往届获奖者）

赛前1周：

• 设备检查（软件安装测试）
• 资料整理（建立模型速查手册）
• 作息调整（适应竞赛时间节奏）

以上就是结合自己的学习经历特别是曾经走过的弯路整理的【小白数学建模学习规划】，通过在2-3个月的系统学习，建立起完整的数学建模能力体系，后续可以应对各类数学建模竞赛，然后在实战当中不断提升。后续笔记我还想分析，想要拿到国一应该做哪些准备，大家现在先打好基础~