《算法很美》3.分治思想 （python实现） 【2】排序算法思想的练习题

例题1.调整数组顺序使奇数位于偶数前面

思路：
运用了快速排序的思路，确定两指针，左指针向右扫描，遇到偶数停下，右指针向左扫描，遇到奇数停下，左右指针对应的数交换。直到左指针右指针交错（左指针大于右指针）

alist=[3,1,2,7,4,9,8,5]
left=0
right=len(alist)-1
done=True
while done:
    while left<=right and alist[left]%2==1:
        left+=1
    while left<=right and alist[right]%2==0:
        right-=1
    if left>right:
        done=False
    else:
        alist[left],alist[right]=alist[right],alist[left]
print(alist)

#原数组：[3,1,2,7,4,9,8,5]
#结果：  [3, 1, 5, 7, 9, 4, 8, 2]

例题2.第k个元素

思路：
一上来的想法是将数组进行排序，排序完后输出对应值，那么即使用最快的快速排序复杂度为O（nlogn）。
为了进一步优化，题目只是问第k个元素，所以我们不需要关心其他元素过于正确的顺序。
借鉴快速排序中找分界点方法的思路，快速排序中找分界点方法把数组分为关于中间值的两部分，分界点的值就是在正确排序数组中的正确顺序，也就是第几小的元素。按照该方法，得到分界点，如果分界点等于k，返回对应值；如果分界点小于k，说明分界点对应的值比第k小的值要小，那么第k小的值在分界点的右边；如果分界点大于k，说明分界点对应的值比第k小的值要大，那么第k小的值在分界点的左边；

（k-1的原因是数组索引是从0开始，k-1索引对应的数才是数组中第k小的值）

def select(alist,first,end,k):
    splitpoint=partition(alist,first,end)
    if spiitpoint==k-1:
        return alist[splitpoint]
    elif spiitpoint<k-1:
        return select(alist,splitpoint+1,end,k)
    else:
        return select(alist,first,splitpoint-1,k)

def partition(alist,first,end):
    pivotvalue=alist[first]
    left=first+1
    right = end
    done = True
    while done:
        while left <= right and alist[left]<=pivotvalue:
            left += 1
        while left <= right and  alist[right]>pivotvalue:
            right -= 1
        if left > right:
            done = False
        else:
            alist[left], alist[right] = alist[right], alist[left]
    alist[first],alist[right]=alist[right],alist[first]
    return right

例题3.超过一半的数字

思路：
方法①：将数组进行排序后，输出索引为数组长度一半对应的值，即为代求值

textlist=[2,8,4,8,3,8,8,8,10,8]
textlist=sorted(textlist)
print(textlist[len(textlist)//2])

方法②：不想排序，参考寻找第k小的元素（这里的k就是数组长度的一半），即为代求值

方法③：消除法
思路：定义两个变量condidate，times，一个记录可能值，一个用来记录出现次数，扫描数组，遇到与condidate相同的，次数加1，遇到不同的次数-1（“消除过程”），减到0时要更新，扫描结束后，返回的condidate就是出现次数大于数组一半的元素

textlist=[2,8,4,8,3,8,8,8,10,8]
condidate=textlist[0]
ctimes=1
for i in range(len(textlist)):
    if ctimes==0:
        condidate=textlist[i]
        ctimes=1
    else:
    	if condidate==textlist[i]:
        	ctimes+=1
    	else:
        	ctimes-=1
print(condidate)

拓展：
假设元素最多出现次数就等于数组长度的一半
消除法遇到极端情况，无法返回正确结果
例如：一个数组为[b,a,c,a,d,a,e,a]，极端情况，各一个就是出现次数为半数的a，两两相同，最后全部被消除。
当a为与最后的位置时，condidate最后为c，不应该能返回condidate,而应该返回a，所以增加一个操作，对最后一个元素计数，如果最后一个元素出现次数为数组长度一半，返回最后一个元素，否则返回candidate

textlist=[1,2,1,3,1,4,1,5]
countofend=0       #添加一个变量来对最后元素计数
condidate=""
ctimes=0
for i in range(len(textlist)):
    if textlist[i]==textlist[-1]:    #扫描元素，若元素等于最后一个元素时，计数+1
        countofend+=1
    if ctimes == 0:
        condidate = textlist[i]
        ctimes = 1
    else:
        if condidate == textlist[i]:
            ctimes += 1
        else:
            ctimes -= 1
    print(condidate,ctimes)
print("*"*10)
#最后一个元素出现次数等于数组长度的一半，最后一个元素是出现次数为数组长度一半
if countofend==len(textlist)//2:
    print(textlist[-2])
#如果不是，condidate代表的元素出现次数为数组长度一半，返回condidate
else:
    print(condidate)

例题4.最小可用的id

题目大意：数组中的数据在1到n中最小缺了哪个
方法①辅助空间+计数法
思路：开辟一个与原数组相同长度的全零数组，扫描原数组，扫描到一个数，就往对应索引的值加1，（如果这个数大于数组长度，说明中间空着很多数）最后扫描新数组，为0的元素对应的索引就是最小可用的id

textlist=[2,3,1,5,4,7,19,20]
countlist=[0]*len(textlist)     #开辟新数组
for i in range(len(textlist)):
    if textlist[i]>len(textlist):
        continue
    else:
        countlist[textlist[i]-1]=1
for index in range(len(countlist)):
    if countlist[index]==0:
        print(index+1)
        break

方法②：

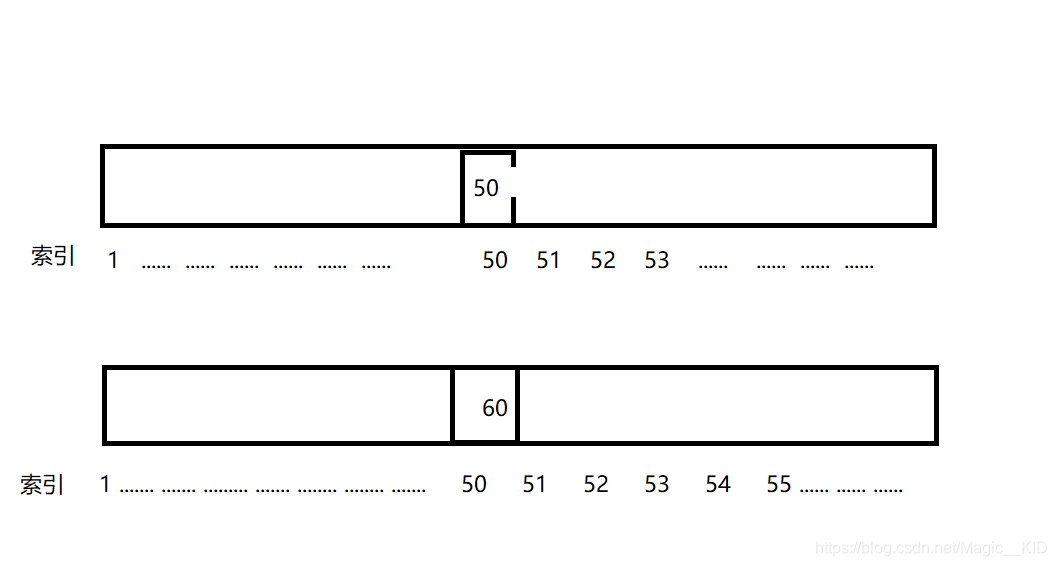
思路：参考选择第k小的方法，查找第k小的元素，例如第50小的元素，恰好为50，说明排序后左边的元素全部排满，都是1到49，最小id要从右边找起；如果大于50，说明左边的元素之间有跳过，最小id要从左边找

textlist=[3,1,2,5,4,6,9,8]
def solution(alist,first,end):
    if first>end:
        return first+1
    midindex=(first+end)//2
    value=select(alist,first,end,midindex+1)
    E=midindex+1                       #期望，找第k小就是k
    if value==E:                       #相等期望，说明最小id在右边
        return solution(alist,midindex+1,end)
    elif value>E:                      #大于期望，说明最小id在右边
        return  solution(alist,first,midindex-1)
print(solution(textlist,0,len(textlist)-1))

例题5.逆序对个数

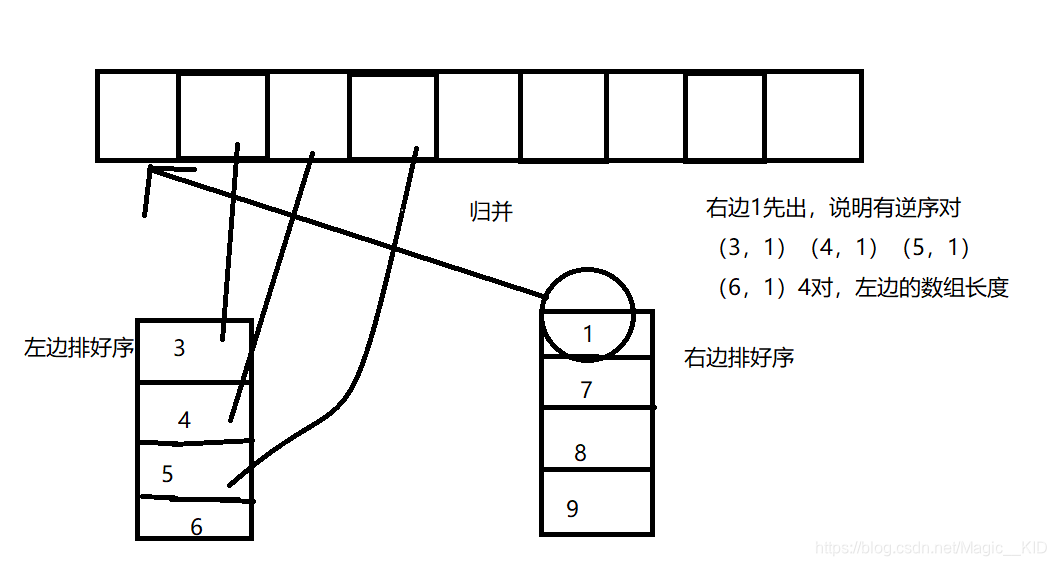
思路：借鉴归并排序，数组分为左右子数组，子数组左右递归分下去，最后左右子数组归并排好序后，如果右边数组元素先出，那么说明左边里的所有元素和它构成逆序对，逆序数加上此时左子数组的长度

textlist=[5,1,3,2,4]
nixu=0
def solve(alist):
    global nixu
    if len(alist)<=1:
        return alist
    else:
        mid=len(alist)//2
        lefthalf=solve(alist[:mid])
        righthalf=solve(alist[mid:])
    merge=[]
    while lefthalf and righthalf:
        if lefthalf[0]<=righthalf[0]:
            merge.append(lefthalf.pop(0))
        else:
            merge.append(righthalf.pop(0))  #如果右边数组元素先出
            nixu+=len(lefthalf)             #逆序数加上此时左子数组的长度
    if lefthalf:
        merge.extend(lefthalf)
    if righthalf:
        merge.extend(righthalf)
    return merge
print(nixu)