机器人的运动范围（数位和、可达解、深度优先遍历、广度优先遍历）

题目要求从0，0开始移动，每次移动的格位要求数位和相加小于阈值。

首先数位和的求法：

private int bitSum(int n) {
        int sum = 0;
        while(n > 0) {
            sum += n % 10;
            n /= 10;
        }
        return sum;
    }

利用取余和除法达到目的。

另一种：
因为该题是从0,0开始递增的，并不需要突兀的求某个大值的数位和，那么就可以通过找到相邻数字数位和的规律来求出。

(i + 1) % 10 != 0 ? si + 1 : si - 8

当前一个数加一取余10等于0，例如：
5和6
6的数位和相比于5直接加一即可
18和19
数位和：9和10

当前一个数加一取余10不为0，例如：
19和20
数位和10和2
29和30
数位和11和3
可以看出后者数位和是前者-8的结果。
实际数位和在此处发生突变是因为后者的9变为0，高位加一故最终结果-8即可。也看出这个计算只能用于两位计算。

可达解：
对于该题，矩阵中共有三种情况，可达解、不可达解、非解
二维矩阵下标是对称分布的，那么其可达解的分布也应是对称的，呈自左上向右下的等腰三角形分布，又因为数位和的突变特性，一个矩形中往往有多个符合解的等腰三角形，但有些解不可达，如图：

借用力扣上大神的图片。
蓝色块为可达解，红色是不满足数位和要求的非解，黄色就是不可达解，但当k值持续增大，蓝色区域与黄色区域连接起来，导致不可达解变为可达解。
如图：

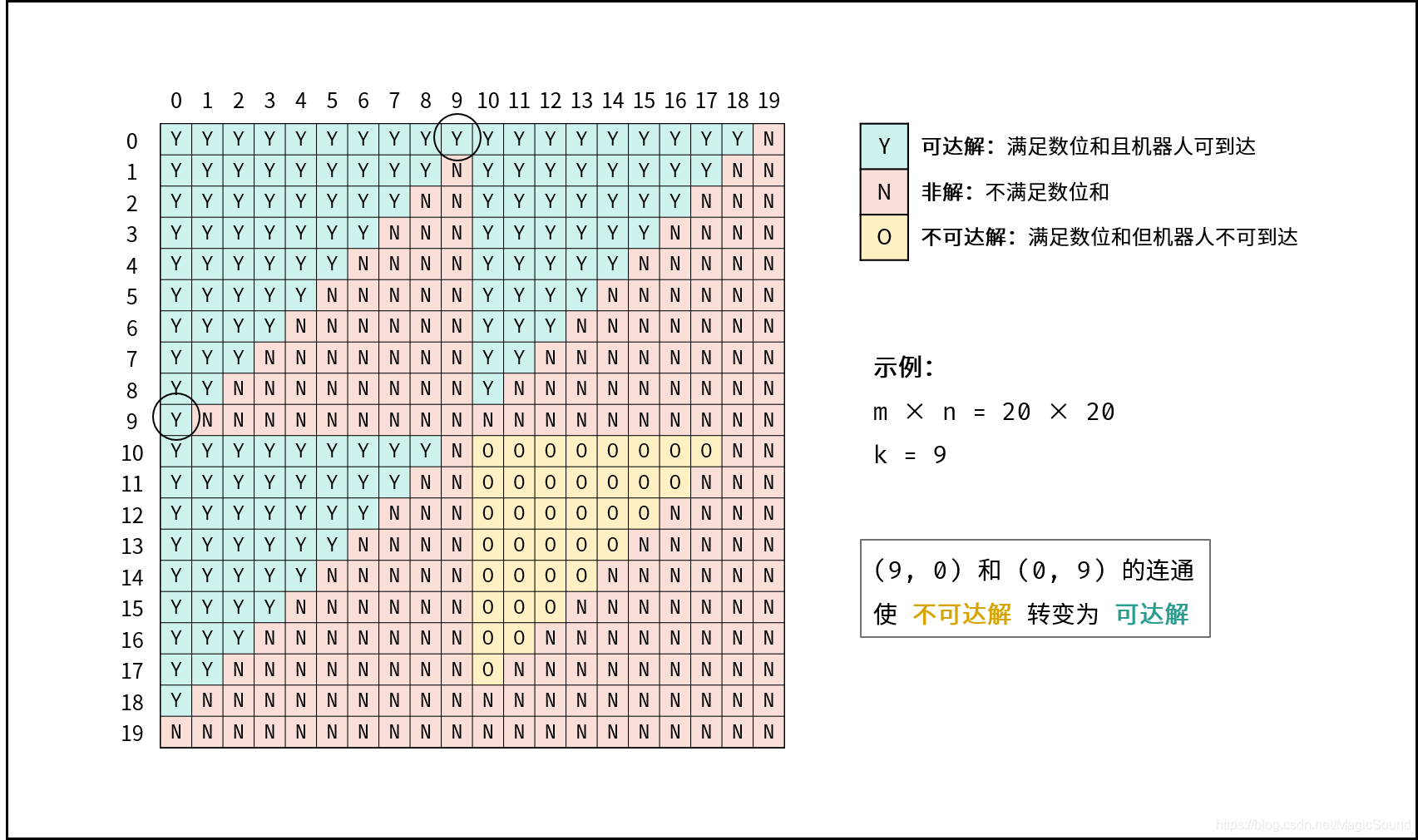
因为可达解与不可达解的交界永远位于右侧或下侧，那么在遍历时候，只需要对节点持续的向右或向下遍历即可遍历出所有的节点。

深度优先遍历DFS：
对矩阵遍历时，先由节点持续向下遍历，当无法继续向下，再向右遍历，当下右都不可以，回溯到前一个节点进行右遍历。

	int m, n, k;
    boolean[][] visited;
    public int movingCount1(int m, int n, int k) {
        this.m = m; this.n = n; this.k = k;
        this.visited = new boolean[m][n];
        return dfs(0, 0, 0, 0);
    }
    public int dfs(int i, int j, int si, int sj) {
        if(i >= m || j >= n || k < si + sj || visited[i][j]) {
            return 0;
        }

        visited[i][j] = true;

        return 1 + dfs(i + 1, j, (i + 1) % 10 != 0 ? si + 1 : si - 8, sj) +
                dfs(i, j + 1, si, (j + 1) % 10 != 0 ? sj + 1 : sj - 8);
    }

广度优先遍历BFS：
该遍历利用队列，把节点加入队列后，取出节点，判断后将其下、右节点都放入队列以供后面使用。

public int movingCount2(int m, int n, int k) {
        boolean[][] visited = new boolean[m][n];
        int res = 0;
        Queue<int[]> queue= new LinkedList<int[]>();
        queue.add(new int[] { 0, 0, 0, 0 });
        while(queue.size() > 0) {
            int[] x = queue.poll();
            int i = x[0], j = x[1], si = x[2], sj = x[3];
            if(i >= m || j >= n || k < si + sj || visited[i][j]) {
                continue;
            }
            visited[i][j] = true;
            res ++;
            queue.add(new int[] { i + 1, j, (i + 1) % 10 != 0 ? si + 1 : si - 8, sj });
            queue.add(new int[] { i, j + 1, si, (j + 1) % 10 != 0 ? sj + 1 : sj - 8 });
        }
        return res;
    }