互补滤波原理:
在四轴入门理论知识那节我们说,加速度计和磁传感器都是极易受外部干扰的传感器,都只能得到2维的角度关系,但是测量值随时间的变化相对较小,结合加速度计和磁传感器可以得到3维的角度关系。陀螺仪可以积分得到三维的角度关系,动态性能好,受外部干扰小,但测量值随时间变化比较大。可以看出,它们优缺点互补,结合起来才能有好的效果。那么三者的数据如何融合呢,接下来介绍互补滤波算法。
互补滤波就是在短时间内采用陀螺仪得到的角度做为最优,定时对加速度采样来的角度进行取平均值来校正陀螺仪的得到的角度。即短时间内用陀螺仪比较准确,以它为主;长时间用加速度计比较准确,这时候加大它的比重,这就是互补了,不过滤波在哪里?加速度计要滤掉高频信号,陀螺仪要滤掉低频信号,互补滤波器就是根据传感器特性不同,通过不同的滤波器(高通或低通,互补的),然后再相加得到整个频带的信号,例如,加速度计测倾角,其动态响应较慢,在高频时信号不可用,所以可通过低通抑制高频;陀螺响应快,积分后可测倾角,不过由于零漂等,在低频段信号不好。通过高通滤波可抑制低频噪声。将两者结合,就将陀螺和加表的优点融合起来,得到在高频和低频都较好的信号,互补滤波需要选择切换的频率点,即高通和低通的频率。
互补滤波原理框图:

加速度计补偿:
假设n系为地理坐标系,b系为机体坐标系,在地理坐标系中,加速度的输出为:
,经过
矩阵转换后的值为:
。在b系中,加速度的测量值为:
,现在
和
都表示在b系中数值向下的向量,由此,我们对这两个向量做向量积(叉积),得到误差:
,利用这个误差来修正
矩阵,于是乎,我们的四元数就在这样一个过程中被修正了。
但是,由于加速度计无法感知Z轴上的旋转运动,所以还需要用地磁计来进一步补偿。现在我们假设旋转矩阵
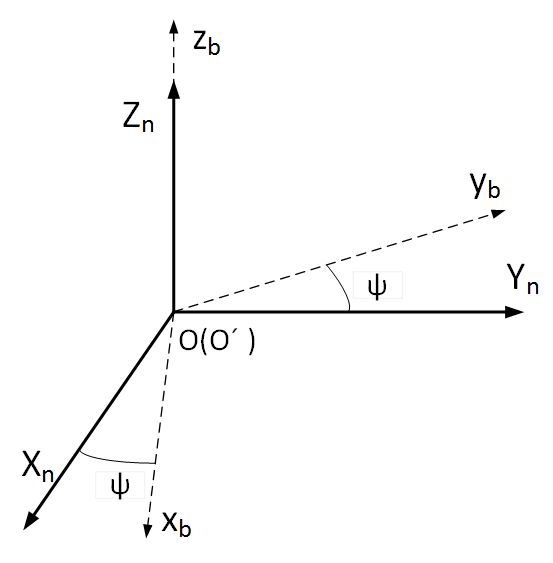
是经过加速度计校正后的矩阵,当某个确定的向量(b系中)经过这个矩阵旋转之后(到n系),这两个坐标系在XOY平面上重合,只是在Z轴旋转上会存在一个偏航角的误差。下图表示的是经过
旋转之后的b系和n系的相对关系。可以明显发现加速度计可以把b系通过四元数法从任意角度拉到与n系水平的位置上,这时,只剩下一个偏航角误差。这也是为什么加速度计误差修正偏航的原因。
地磁计补偿:
现在我们反过来从b系到n系,假设地磁计在b系中的输出为:
,经过
的转换后得到:
。由于
是经过加速度计修正过的旋转矩阵,因此该旋转矩阵只在Z轴上存在一个偏航的误差,这就导致
中的hy不为零。如果
不存在误差,这里的hy应该为0。在n系中,地磁方向与x轴呈一个角度,与z轴呈一个角度,这里我们让x轴对准北边,那么地磁向量为:
。在n系的XOY平面上(水平面),
的投影为:Sqrt(bx * bx),
的投影为:Sqrt((hx * hx)+ (hy * hy))。由于
存在的偏航误差,导致
的hy不为零,这就是说现在得到的
是真实的地磁向量绕Z轴旋转一定的角度后得到的。但由于是绕Z轴旋转,所以该地磁向量在XOY平面上(n系)投影的大小必定相同,所以有bx^2= hx^2+hy^2,我们求出了地磁向量在X轴方向的真实值。而
得到hz就是地磁向量在Z轴方向上的真实值,我们不做改变,令bz=hz即可。经过这样处理之后我们得到
,这个地磁向量就是地磁的真实值,类似于重力加速度的
。接着把
经过
变换后到b系中得到:
。
与
向量积求误差,再次修正
这样就完成了一次地磁计的补偿。
将加速度计没能做到的z轴上的旋转修正,通过地磁计在XOY平面上的地磁力相同原理,得到了修正。于是乎,Pitch和Roll通过加速度计修正,然后在这个基础之上(该地磁计补偿方法必须依靠加速度计修正提供一致的XOY平面,才会有bx^2= hx^2+hy^2等式成立),Yaw通过地磁计来补偿,最终得到了没有偏差的实时姿态(也就是由四元数组成的旋转矩阵)。
代码分析:
// 加速度计、地磁计、陀螺仪数据融合,更新四元数
/*
[gx,gy,gz]为陀螺仪的测量值
[ax,at,az]为加速度的测量值
[mx,my,mz]为地磁计的测量值
*/
void AHRSupdate(float gx, float gy, float gz, float ax, float ay, float az, float mx, float my, float mz)
{
float norm;
float hx, hy, hz, bx, bz;
float vx, vy, vz, wx, wy, wz;
float ex, ey, ez;
// 定义一些辅助变量用于转换矩阵
float q0q0 = q0*q0;
float q0q1 = q0*q1;
float q0q2 = q0*q2;
float q0q3 = q0*q3;
float q1q1 = q1*q1;
float q1q2 = q1*q2;
float q1q3 = q1*q3;
float q2q2 = q2*q2;
float q2q3 = q2*q3;
float q3q3 = q3*q3;
// 归一化加速度计和地磁计的度数
norm = sqrt(ax*ax + ay*ay + az*az);
ax = ax / norm;
ay = ay / norm;
az = az / norm;
norm = sqrt(mx*mx + my*my + mz*mz);
mx = mx / norm;
my = my / norm;
mz = mz / norm;
//将b系中的地磁计分量[mx,my,mz]转换到n系,得到[hx,hy,hz]
hx = 2*mx*(0.5 - q2q2 - q3q3) + 2*my*(q1q2 - q0q3) + 2*mz*(q1q3 + q0q2);
hy = 2*mx*(q1q2 + q0q3) + 2*my*(0.5 - q1q1 - q3q3) + 2*mz*(q2q3 - q0q1);
hz = 2*mx*(q1q3 - q0q2) + 2*my*(q2q3 + q0q1) + 2*mz*(0.5 - q1q1 - q2q2);
//得到n系中的地磁向量的真实值[bx,bz,by],其中by=0
bx = sqrt((hx*hx) + (hy*hy));
bz = hz;
//n系中的地磁向量[bx,by,bz]转换到b系中,得到[wx,wy,wz]
wx = 2*bx*(0.5 - q2q2 - q3q3) + 2*bz*(q1q3 - q0q2);
wy = 2*bx*(q1q2 - q0q3) + 2*bz*(q0q1 + q2q3);
wz = 2*bx*(q0q2 + q1q3) + 2*bz*(0.5 - q1q1 - q2q2);
//n系中重力加速度[0,0,1]转换到b系中得到三个分量[vx,vy,vz]
vx = 2*(q1q3 - q0q2);
vy = 2*(q0q1 + q2q3);
vz = q0q0 - q1q1 - q2q2 + q3q3;
//计算[wx,wy,wz] X [mx,my,mz],[ax,at,az] X [vx,vy,vz],得到两个误差后求和
ex = (ay*vz - az*vy) + (my*wz - mz*wy);
ey = (az*vx - ax*vz) + (mz*wx - mx*wz);
ez = (ax*vy - ay*vx) + (mx*wy - my*wx);
//PI控制器中的积分部分
exInt = exInt + ex*Ki* (1.0f / sampleFreq);
eyInt = eyInt + ey*Ki* (1.0f / sampleFreq);
ezInt = ezInt + ez*Ki* (1.0f / sampleFreq);
//误差经过PI控制器后输出,然后补偿到角速度的三个分量,Kp、Ki是需要调节的参数
gx = gx + Kp*ex + exInt;
gy = gy + Kp*ey + eyInt;
gz = gz + Kp*ez + ezInt;
//一阶龙格库塔法更新四元数
q0 = q0 + (-q1*gx - q2*gy - q3*gz)*halfT;
q1 = q1 + (q0*gx + q2*gz - q3*gy)*halfT;
q2 = q2 + (q0*gy - q1*gz + q3*gx)*halfT;
q3 = q3 + (q0*gz + q1*gy - q2*gx)*halfT;
// 归一化四元数
norm = sqrt(q0*q0 + q1*q1 + q2*q2 + q3*q3);
q0 = q0 / norm;
q1 = q1 / norm;
q2 = q2 / norm;
q3 = q3 / norm;
} 参考:https://blog.youkuaiyun.com/qq_21842557/article/details/50993809
https://blog.youkuaiyun.com/superrunner_wujin/article/details/55809648
https://legacy.gitbook.com/book/nephen/direction-cosine-matrix-imu-theory/details
https://blog.youkuaiyun.com/qq_21842557/article/details/50993809





















 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








