决策树

一.概念

决策树是一种树形结构，其中每个内部节点表示一个属性上的判断，每个分支代表一个判断结果的输出，最后每个叶节点代表一种分类结果，本质是一颗由多个判断节点组成的树

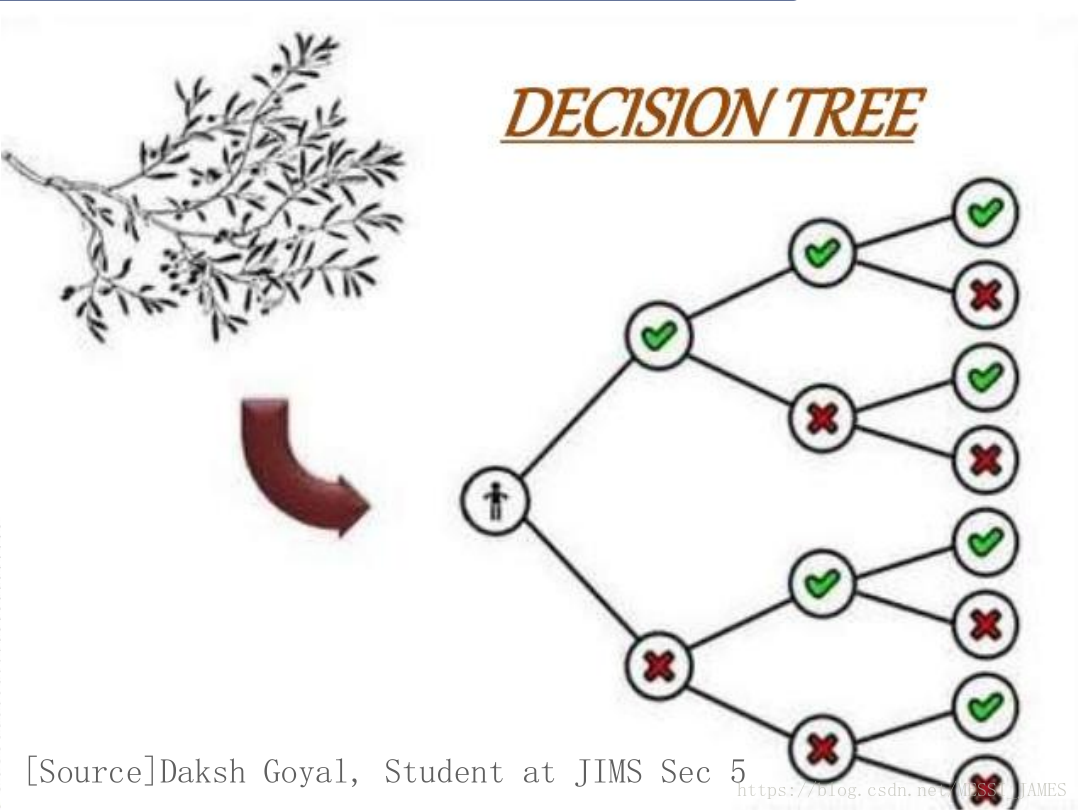
二.划分依据

1.熵

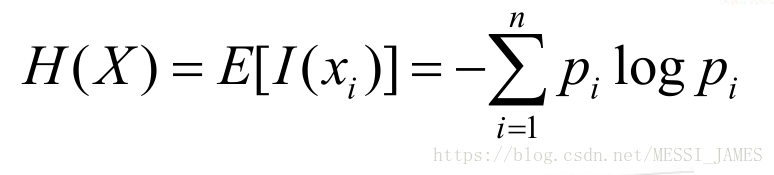
（1）当系统的有序状态一致时，数据越集中的地方熵值越小，数据越分散的地方熵值越大。这是从信息的完整性上进行的描述。
（2）当数据量一致时，系统越有序，熵值越低；系统越混乱或者分散，熵值越高。这是从信息的有序性上进行的描述。

2.信息增益及增益率

信息增益值的大小是相对于训练集而言的

以某特征划分数据集前后的熵的差值。熵可以表示样本集合的不确定性，熵越大，样本的不确定性就越大。因此可以
使用划分前后集合熵的差值来衡量使用当前特征对于样本集合D划分效果的好坏。
信息增益 = entroy( 前) - entroy( 后)

信息增益=总体熵-样本熵x权重

3.基尼值和基尼指数

1.基尼值Gini（D）
从数据集D中随机抽取两个样本，起类别标记不一致的概率，Gini（D）值越小，数据集D的纯度越高。

2.基尼指数Gini_index（D）
一般，选择使划分后基尼系数最小的属性作为最优化分属性

4.信息增益比

信息增益是划分训练数据集的特征，经验熵大时，信息增益会偏大，反之偏小。而信息增益比可以解决这一问题。
`

三.决策树的生成算法

1.ID3算法

ID3算法只有树的生成。所以该算法容易产生过拟合。

2.C4.5算法

信息增益（Info Gain）用于ID3，Gini用于CART，信息增益率（Info Gain Ratio）用于C4.5。

四.基本流程

1.决策树构建的基本步骤：

1）. 开始讲所有记录看作一个节点
2.） 遍历每个变量的每一种分割方式，找到最好的分割点
3.） 分割成两个节点N1和N2
4.） 对N1和N2分别继续执行2-3步，直到每个节点足够“纯”为止。

2.决策树的变量可以有两种

1） 数字型（Numeric）：变量类型是整数或浮点数，如前面例子中的“年收入”。用“>=”，“>”,“<”或“<=”作为分割条件（排序后，利用已有的分割情况，可以优化分割算法的时间复杂度）。
2） 名称型（Nominal）：类似编程语言中的枚举类型，变量只能重有限的选项中选取，比如前面例子中
的“婚姻情况”，只能是“单身”，“已婚”或“离婚”，使用“=”来分割。

3.如何评估分割点的好坏？

如果一个分割点可以将当前的所有节点分为两类，使得每一类都很“纯”，也就是同一类的记录较多，那
么就是一个好分割点。

四.常见决策树类型及剪枝

1.常见决策树类型比较

2.决策树的剪枝

（1）为什么要剪枝

横轴表示在决策树创建过程中树的结点总数，纵轴表示决策树的预测精度。
实线显示的是决策树在训练集上的精度，虚线显示的则是在一个独立的测试集上测量出来的精度。
分析:随着树的增长， 在训练样集上的精度是单调上升的， 然而在独立的测试样例上测出的精度先上升后下降。
有以下三个原因：
•原因1：噪声、样本冲突，即错误的样本数据。
•原因2：特征即属性不能完全作为分类标准。
•原因3：巧合的规律性，数据量不够大。

（2）常用的剪枝方法

1.1 预剪枝：
（1）每一个结点所包含的最小样本数目，例如10，则该结点总样本数小于10时，则不再分；
（2）指定树的高度或者深度，例如树的最大深度为4；
（3）指定结点的熵小于某个值，不再划分。随着树的增长， 在训练样集上的精度是单调上升的， 然而在独立的测试样 例上测出的精度先上升后下降。
1.2 后剪枝：
后剪枝，在已生成过拟合决策树上进行剪枝，可以得到简化版的剪枝决策树。
（1）REP-错误率降低剪枝
（2）PEP-悲观剪枝
（3）CCP-代价复杂度剪枝
（4）MEP-最小错误剪枝