第08周：吴恩达 Andrew Ng 机器学习

13 聚类

聚类算法是学习的第一个无监督学习算法，它所用到的数据是不带标签的。

13.1 无监督学习

什么是无监督学习？

在无监督学习中，所有的数据不带标签，而无监督学习要做的就是将这一系列无标签的数据输入到算法中，并找到一些隐含在数据中的结构。

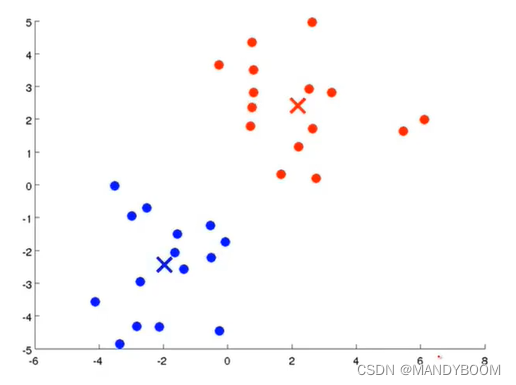
如下图，都是一些没有标签的样本点，无监督学习算法将他们分为了两簇，分别使聚在一起的点作为了一类，所以也叫聚类算法（无监督学习算法的一种）。

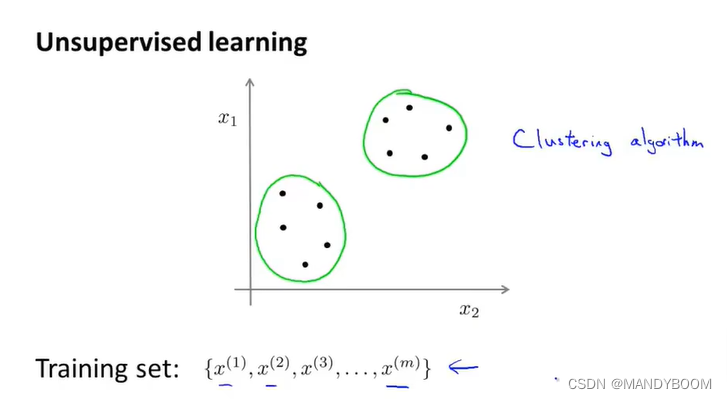
聚类可以应用在市场分割、社交网络分析、组织计算机集群、了解银河系的构成等领域。

13.2 K-Means算法

K-Means（K均值）算法是现在最热门最为广泛运用的聚类算法，它也是一个迭代算法，它可以做两件事，一是簇分配，二是移动聚类中心。簇分配就是算法会遍历所有点，判断它与哪个聚类中心离得近，就将其分配给两个聚类中心之一。移动聚类中心就是，分配完所有点后，将聚类中心移动到簇内所有点的均值处。

用图像来说明K-Means算法，假设有一个无标签的数据集，需要将它分成两个簇，执行K-Means算法的操作如下：

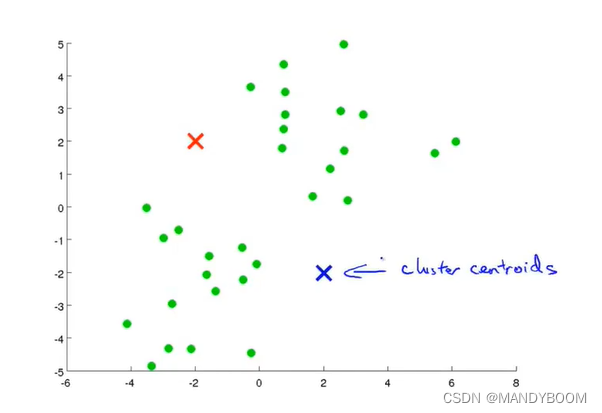
• 随机生成两点（聚类中心），图中的红色和蓝色的× 
• 内循环

                 簇分配

                 移动聚类中心

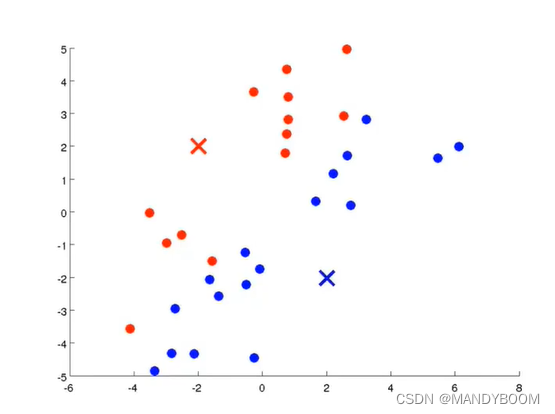
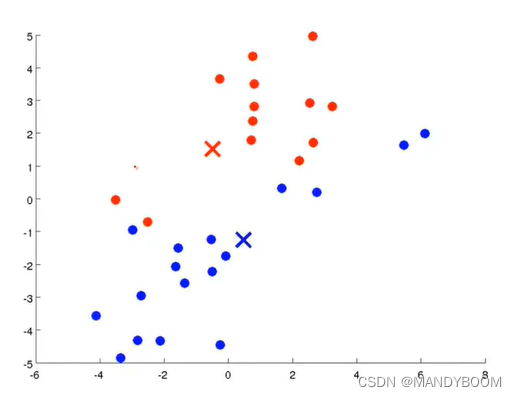
 文字说明K-Means算法

• 输入：K(想要分成K簇)、训练集（无标签的x，n维向量）
• 随机初始化K个聚类中心μ1,μ2，…，μk，然后对每个训练样本簇分配（用c^(i)表示样本点离哪个聚类中心近）；接着移动聚类中心，对每个聚类中心求它所在簇的所有点值的均值。（如果一个簇内除了聚类中心，没有样本点，常见的作法就是移除这个聚类中心或者重新随机初始化）

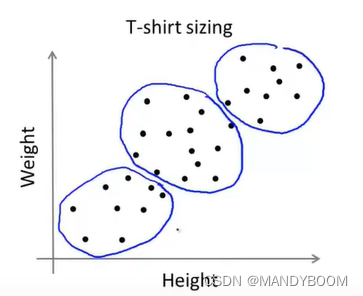
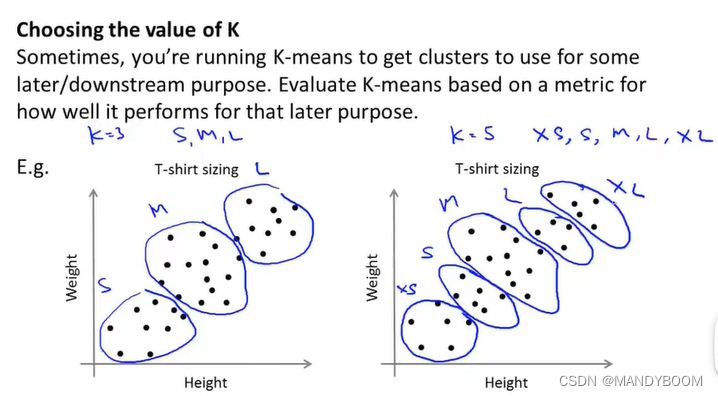
K-Means算法还可以解决分离不佳的簇的问题，比如下图，根据身高体重定制三种大小的T恤，虽然数据集并不明显的聚类，但是K-Means算法还是可以将其分为几个簇。

13.3 优化目标 

在之前学的所有算法都有一个优化目标函数或者最小化的代价函数。K-Means均值函数也有。

在引入优化目标前，要知道三个变量：、、。表示样本点i所属离得最近得聚类中心得序号，表示第k个聚类中心所在位置的均值。比如，。

那么代价函数（也叫失真代价函数）与优化目标如下：

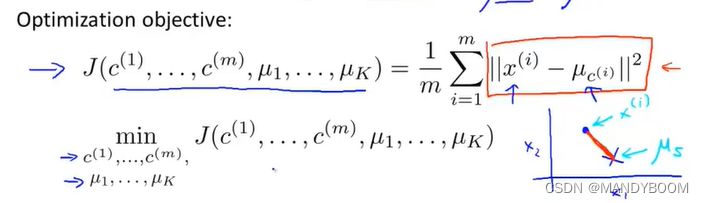
 K-均值迭代算法中，第一个循环（分簇）是用于减小𝑐(𝑖)引起的代价，而第二个循环（调整聚类中心）则是用于减小𝜇𝑖引起的代价。迭代的过程一定会是每一次迭代都在减小代价函数，不然便是出现了错误。

 13.4 随机初始化以及避开局部最优

随机初始化聚类中心：

•  首先设置K个簇，此处得K<m(训练样本)
• 随机挑选K个训练样本，让对应的μ等于所选的训练样本

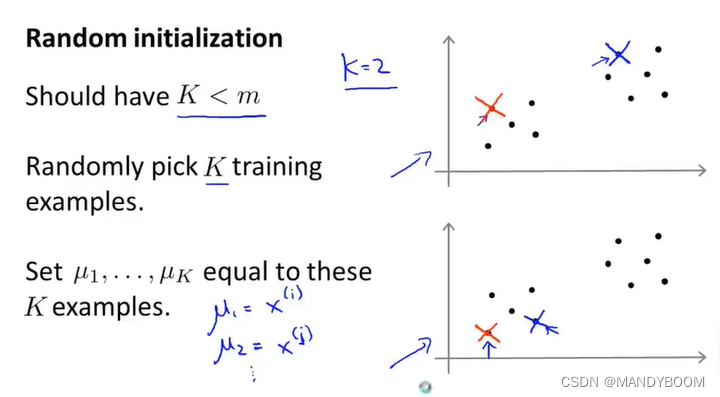
由于聚类中心是随机初始化的，所以K-Means算法最后得出的结果也可能是不一样的，可能会落在局部最优 。比如下图的下面两幅图像。

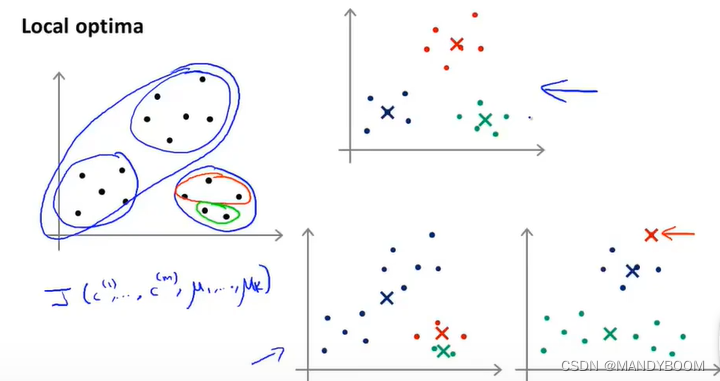
解决这种问题，可以尝试多次随机初始化。

具体操作（加入要初始化100次，并运行100次K-Means算法），那就要执行下面得循环100次：初始化、运行算法得到、一系列聚类结果、利用这些结果计算代价函数。完成100次循环后，在一百种分簇得方式中选择代价函数值最小的 一组。上述这种方法适用于K比较小得情况，如果K很大，需要循环成百上千，那么多次随机初始化这种方法就不会有太大改善。

 13.5 如何选取聚类数量（K值）

最常见的办法：观察可视化图像手动选择K值。因为是无监督学习，所以正确答案不是固定的。但是也有一些其他方法。

第一种方法：肘部法则：改变K值，计算代价函数，画出图像，选择‘肘部’，拐弯处的K作为聚类数量。

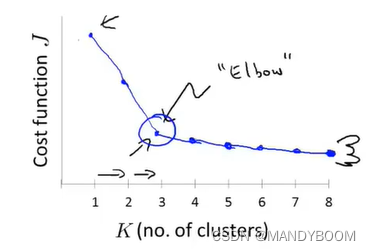
但是在实际问题中，画出来的肘部图可能没有上图这么清晰得拐点，就像下图一样，所以肘部法则并不能很好的解决任何问题 。

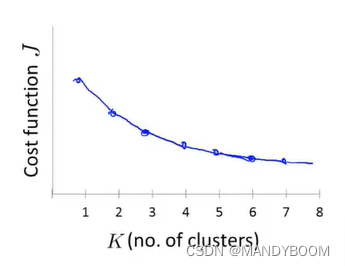
第二种方法：看K选多少能更好地应用于后续目的 。比如制作T恤得尺寸大小，看K为多少更能满足顾客需求。