理解多维高斯分布

前言

在数理统计和机器学习中，经常用到高斯分布，这里根据网上的资源和理解，对多维高斯分布做一个小总结。如有谬误，请联系指正。转载请注明出处。

$\nabla$ 联系方式：

e-mail: FesianXu@gmail.com

QQ: 973926198

github: https://github.com/FesianXu

知乎专栏: 计算机视觉/计算机图形理论与应用

微信公众号：

---

一维高斯分布

标准的一维高斯分布是0均值和单位方差的，数学形式如(1)：
$$p(x)=\frac{1}{\sqrt{2\pi }}exp(-\frac{x^2}{2})\text{\hspace{1em}(1)}$$
为了扩展成一般的一维高斯分布，我们引入一个线性变换$x:=A(x-\mu )$，结合(1)，有：
$$\begin{array}{rl}p(x)& =\frac{|A|}{\sqrt{2\pi }}exp(-\frac{A^2(x-\mu {)}^2}{2})\end{array}\text{\hspace{1em}(2)}$$
令$\sigma =1/A$，式(2)变为:
$$p(x)=\frac{1}{\sigma \sqrt{2\pi }}exp(-\frac{(x-\mu {)}^2}{2{\sigma }^2})\text{\hspace{1em}(3)}$$
从这里可以看出$A$和$\sigma$存在关系。在系数前乘上$|A|$是为了整个分布的积分为1。这里的$|\cdot |$表示绝对值，在多变量下，则表示行列式。

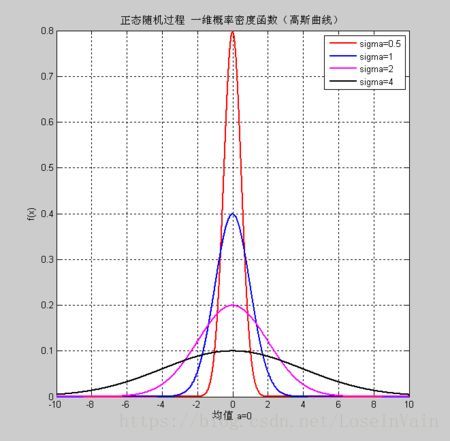
在一维高斯分布上，通过调整均值$\mu$和方差${\sigma }^2$可以调整分布的形状，使得其向左右平移，或者拉伸其"顶峰"。

多维高斯分布

多维高斯分布其变量为$n$维变量，每个变量之间可能会存在关系，为了描述这种关系，我们引入了协方差矩阵$\Sigma$，其大小为$n\times n$，其中每一个元素为:
$$\begin{array}{rl}{\Sigma }_{i,j}& =conv(X_i,X_j)\\ & =E(X_i{X}_j)-E(X_i)E(E_j)\end{array}\text{\hspace{1em}(4)}$$

我们首先看看标准二维高斯分布的数学表达式(5)，因为是标准二维高斯分布，所以每个变量之间是独立的:
$$p(x,y)=p(x)p(y)=\frac{1}{2\pi }exp(-\frac{x^2+y^2}{2})\text{\hspace{1em}(5)}$$
为了向量化公式，用向量$\text{v}=[xy{]}^T$，有：
$$p(\text{v})=\frac{1}{2\pi }exp(-\frac{1}{2}{\text{v}}^T\text{v})\text{\hspace{1em}(6)}$$
这个时候，用$\text{v}=\text{A}(\text{x}-\mu )$，其中的$\text{A}$为$\text{v}$中每个分量的线性组合系数，也就是说$\text{A}$表示了每个变量的线性关系。有：
$$p(\text{v})=\frac{|\text{A}|}{2\pi }exp(-\frac{1}{2}(\text{x}-\mu {)}^T{\text{A}}^T\text{A}(\text{x}-\mu ))\text{\hspace{1em}(7)}$$
用$\Sigma =({\text{A}}^T\text{A}{)}^{-1}$表示其协方差，其中$|\text{A}|$为行列式，有：
$$p(\text{v})=\frac{1}{2\pi |\Sigma {|}^{1/2}}exp(-\frac{1}{2}(\text{x}-\mu {)}^T{\Sigma }^{-1}(\text{x}-\mu ))\text{\hspace{1em}(8)}$$
当维度大于2时，情形类似，$n$维的高斯分布公式为：
$$\begin{gathered} p(\text{v})=\frac{1}{(2\pi {)}^{n/2}|\Sigma {|}^{1/2}}exp(-\frac{1}{2}(\text{x}-\mu {)}^T{\Sigma }^{-1}(\text{x}-\mu )) \\ \text{v}\in {\mathbb{R}}^n\text{\hspace{1em}(9)} \end{gathered}$$

多维高斯分布的图像性质

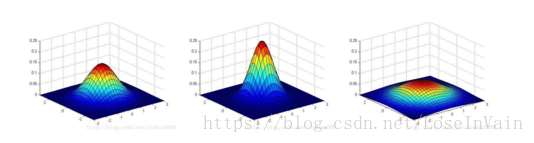
以上三个图形的期望都为：$\mu =[0,0{]}^T$，最左端图形的协方差$\Sigma =I$，中间的$\Sigma =0.6I$，最右端的$\Sigma =2I$，我们可以看出：当变小时，图像变得更加“瘦长”，而当增大时，图像变得更加“扁平”。

Reference

1. 斯坦福大学机器学习——高斯判别分析
2. 多维高斯分布是如何由一维发展而来的？