2025年SEVC SCI2区，自适应Q学习模因算法Q-SAMA+多AGV调度问题，深度解析+性能实测

---

1.摘要

本文解决了在实际生产车间中调度多个自动引导车（AGV）的问题，旨在最小化运输成本。为了解决这个问题，本文提出了一种自适应Q学习模因算法（Q-SAMA），采用改进的最近邻任务划分启发式方法生成优质解。此外，集成了Q学习来选择合适的邻域操作算子，从而增强算法的探索能力。为了防止算法陷入局部最优，提出了重启策略。为了使Q-SAMA适应搜索过程中的不同阶段，不再使用传统的交叉和变异概率，而是根据种群的集中程度和个体适应度之间的稀疏关系自适应地获得概率。

2.问题描述和表述

制造车间中多个工作站以矩阵形式分布，每个工作站由若干数控机床和物料缓冲区组成。数控机床通过消耗物料加工产品，物料缓冲区则负责存储生产物料。当物料剩余量达到下限时，工作站向控制系统发出请求，称为呼叫时间，发出请求的工作站称为呼叫工作站。控制系统接到请求后，会调度一个AGV来运输物料。AGV在接到指令后，从仓库出发，按计划将物料送至呼叫工作站，并在卸货后返回仓库，该过程构成了AGV的运输路线，并产生相应的运输距离成本。

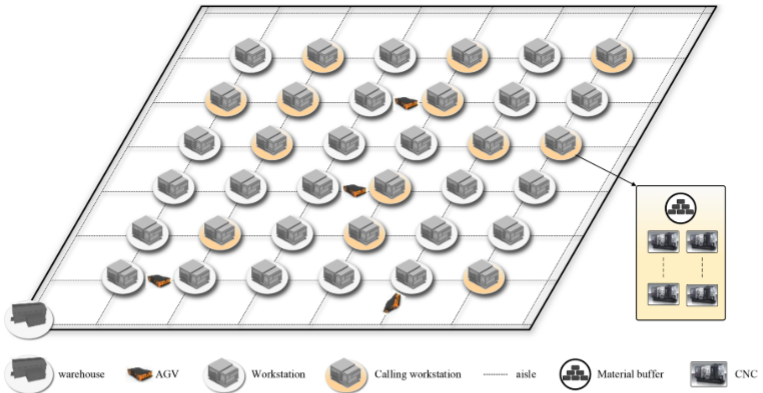
AGVDP数学模型

AGVDP距离度量采用曼哈顿距离，AGV在任务点$i$处的卸货量由两部分组成。一部分是在呼叫时刻任务$i$的物料缓冲区已使用的量，且数控机床在控制系统接受呼叫后以及AGV运输过程中持续消耗物料。另一部分是从任务$i$呼叫时刻到任务$i$实际交付时刻之间消耗的物料量。

3.自适应Q学习模因算法Q-SAMA

Moscato于1989年首次提出了模因算法（Memetic Algorithm, MA）的概念。MA结合了群体智能和个体进化，通常从初始化的种群开始，经过选择、交叉、变异和局部搜索等迭代操作，直到满足停止条件。本文提出了一种改进MA（Q-SAMA）来解决AGVDP问题，以最小化运输成本。

解表示方式

本文使用一种简单但有效的排序方式来表示解，该排序基于调度序列，其中没有缺失或重复的任务。假设有$f$个任务和$h$个AGV。解使用一个一维向量表示：

$$(c_1,\dots ,c_i,0,c_{i+1},\dots ,c_j,0,c_{j+1},\dots ,c_f)$$

其中，$h_r$为车间任务$r$，$h$个AGV采用$h-1$个0。

假设车间中有三个AGV运输九个任务，G1、G2和G3分别是三个AGV的编号，（1, 2, 3, 4, 5, 6, 7, 8, 9）是任务的标号。G1的AGV路线为（5, 7, 1），即G1从仓库出发，先完成任务5，然后是任务7、任务1，最后返回仓库。G2和G3的AGV路线分别为（2, 8, 3）和（9, 4, 6）。两个相邻的AGV路线由0分隔，因此解的表示为（5, 7, 1, 0, 2, 8, 3, 0, 9, 4, 6）。

改进最近邻任务划分启发式算法

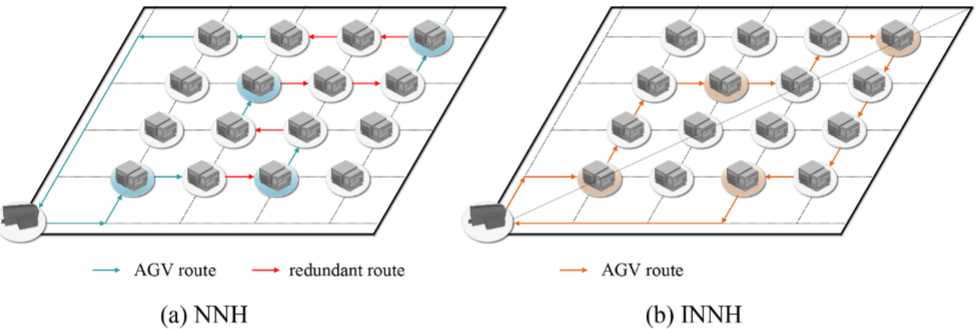
为了解决AGVDP问题，Zou提出了一种基于最近邻的启发式算法（NNH）。在初始化阶段，满足时间约束和容量约束的条件下，算法将离当前任务点$i$（或仓库）最近的任务点j添加到当前AGV路线中。此过程重复进行，直到当前AGV的路线分配完成。接着，调度新的AGV来分配剩余任务，直到所有任务被分配，同时确保每个任务只被分配一次。

NNH的核心思想是贪心策略，它只关注当前的局部最优解，而没有全面考虑其他可能的情境。这种做法可能导致AGV的行驶路线低效，从而增加不必要的行驶距离成本。本文提出了改进最近邻任务划分启发式算法（INNH），通过一条直线将车间区域分为两部分，这条直线连接仓库和距离仓库最远的任务点。集合AU包括位于直线以上的任务点（包括直线上的任务点），而集合BU包括位于直线以下的任务点。分别对AU和BU使用基于最近邻的启发式算法进行任务划分。

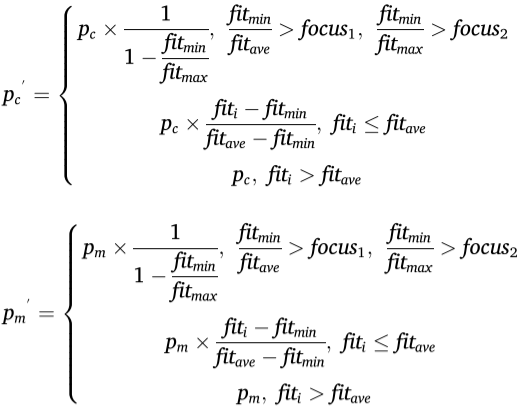
自适应交叉和变异算子

传统交叉和变异操作算子使用固定的概率，这对于某些个体来说不够公平，也不利于种群的有效进化。因此，本文提出了自适应交叉概率和变异概率。

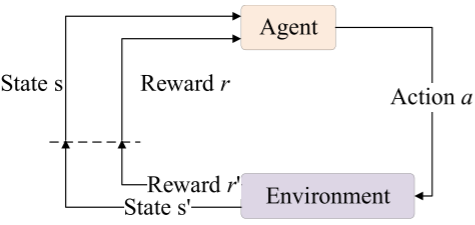
Q-learning局部搜索

Q-learning是一种有效的优化机制，用于解决强化学习中的复杂问题。Q-learning通过智能体与环境的交互，获得反馈奖励值并能帮助算法智能地选择邻域结构。在本文中，Q-learning用于选择邻域操作算子。当前解被视为状态，六种不同的邻域结构作为动作。

重启阶段

为了增强种群的多样性，采用了重启策略。通过变量记录最优值保持不变的代数，并且设置重启阈值。当触发重启机制时，算法会从存档集中随机选择一个解，进行4种算子处理：

• 算子1：根据任务数量随机生成一个(0/1)数组，每个任务与一个0或1对应。对应1的任务保持原位置，对应0的任务随机分配到其他位置；

• 算子2：随机选择一个任务，保持该任务右侧不变，左侧任务随机打乱；

• 算子3：随机选择一个任务，保持该任务左侧不变，右侧任务随机打乱；

• 算子4：随机选择两个任务，位于这两个任务之间的任务随机打乱。

4.结果展示

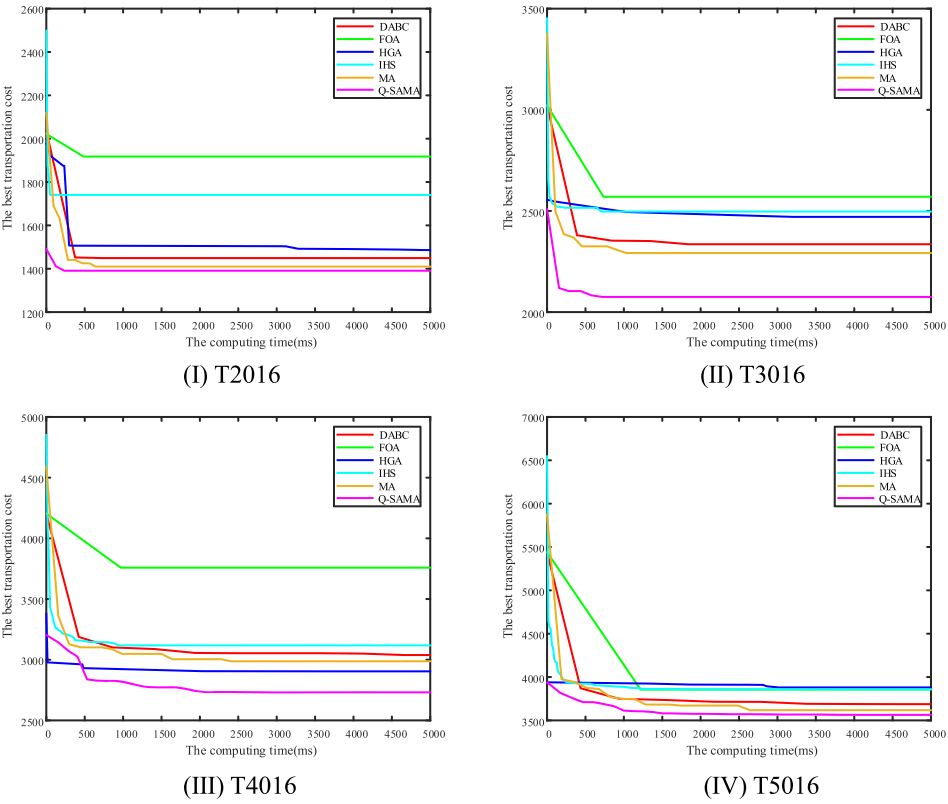
5.参考文献

[1] Zheng C Z, Sang H Y, Xing L N, et al. A self-adaptive memetic algorithm with Q-learning for solving the multi-AGVs dispatching problem[J]. Swarm and Evolutionary Computation, 2024, 90: 101697.

6.算法辅导·应用定制·读者交流