平面几何习题

Q1判断三点顺序

利用了力矩的性质

关于力矩前面讲过了

往期回顾 

平面上的三个点A(0,0),B(1,0),C(0,2)。按A->B->C是逆时针,按C-B-A是顺时针。
给你平面三点的顺序，请你判断是逆时针、顺时针还是共线。

输入格式

输入有若干行，每行有6个整数：X1、Y1、X2、Y2、X3、Y3表示你要顺序经过的三个点。

输出格式

每行输出一个结果，顺时针就输出“Clockwise”，逆时针就输出“Anticlockwise”，共线输出"Collineation"。

输入样例

0 0 1 0 0 2
0 2 1 0 0 0

输出样例

Anticlockwise
Clockwise

一开始看一脸懵，什么是共线？？？、

参考博客

原来不止空间向量有叉乘，平面也有（叫做叉积） ……

可以理解为积之差

大逆小顺0与共

#include <iostream>
#include <iomanip>
#include<cstdio>
#include<cmath>
#include<stack>
#include<algorithm>
using namespace std;

typedef unsigned long long ull;
const ull MOD=0x3f3f3f3f3f;
const double PI=3.1415926;

int main()
{
    double a,b,c;
    int x1,x2,y1,y2,x3,y3;
    int n;
    int x,y;
    while(cin>>x1>>y1>>x2>>y2>>x3>>y3)
    {
        double sum=(x2-x1)*(y3-y1)-(y2-y1)*(x3-x1);
        if(sum>0)
            cout<<"Anticlockwise";
        else if(sum==0)
            cout<<"Collineation";
        else
            cout<<"Clockwise";
        cout<<endl;
    }

    return 0;
}

画个图吧

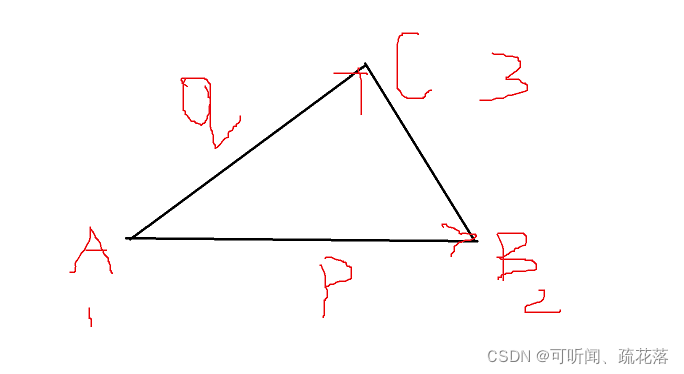
 平面上的叉积

Q2判断两直线是否相交

输入线段AB、CD的两端点，判断两线段是否相交（包含端点）。

输入格式

有多组数据，每组数据两行，第一行四个整数，分别表示A、B两点坐标，第二行四个整数，分别表示C、D两点坐标。

输出格式

如果线段AB与线段CD相交，输出yes，否则输出no。

输入样例 

0 1 1 1
1 0 2 1
1 0 2 1
0 1 2 0
0 0 0 1
1 0 0 0

输出样例 

no
yes
yes

分两步

1.排斥实验

排除线段对应矩形都没有相交的情况（包括在一条线上但是不相交的情况）

简而言之：

某一行（A、B为一行，C、D为另一行）最大的x不小于另一行最小的x

……………………………………………………...y……………………...y

都满足则通过排斥实验 

2.跨立实验

判断是否彼此相交

简而言之：

拿出D或C判断得AB在CD两侧

拿出A或B判断得CD在AB两侧就够了 

工具就是叉积

大家都用结构体表示点，我也觉得挺易于阅读，也用结构体了

#include<iostream>
#include<iomanip>
#include<cstdio>
#include<cmath>
#include<stack>
#include<algorithm>
using namespace std;

typedef unsigned long long ull;
const ull MOD=0x3f3f3f3f3f;
const double PI=3.1415926;

int a[100010];
struct text
{
    double x;
    double y;
} A,B,C,D;
//AB是第一行
//CD是第二行
bool abstract(text A,text B,text C,text D)
{
    if(     max(A.x,B.x)<min(C.x,D.x)||
            max(C.x,D.x)<min(A.x,B.x)||
            max(A.y,B.y)<min(C.y,D.y)||
            max(C.y,D.y)<min(A.y,B.y)
      )
        return false;
    return true;//默认
}
bool judge(text A,text B,text C,text D)
{
    //A  C 两点为代表
    if(     (
                ((C.y-A.y)*(B.x-A.x)-(B.y-A.y)*(C.x-A.x))*//AB叉AC*AB叉AD
                ((D.y-A.y)*(B.x-A.x)-(B.y-A.y)*(D.x-A.x))<=0
            )
            &&
            (
                ((B.y-C.y)*(D.x-C.x)-(D.y-C.y)*(B.x-C.x))*//CD叉CB*CD叉CA
                ((A.y-C.y)*(D.x-C.x)-(D.y-C.y)*(A.x-C.x))<=0
            )
      )
      return true;

    return false;


    }
int main()
{
    while(cin>>A.x>>A.y>>B.x>>B.y>>C.x>>C.y>>D.x>>D.y)
    {
        if(abstract( A, B, C, D))
        {
            if(judge(A,B,C,D))
            {
                cout<<"yes"<<endl;
            }
            else
            {
                cout<<"no"<<endl;
            }
        }
        else//不相交
        {
            cout<<"no"<<endl;
        }
    }

    return 0;
}

nice！