刚开始根本读不懂题目。。。
官方题解
We need to find such x and
y that the value of 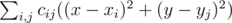 is minimum possible.
This expression can be rewritten as
is minimum possible.
This expression can be rewritten as 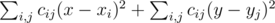 . Note that the first part doesn't depend
on y and the second part doesn't depend on
x, so we can minimize these parts separately. Here is how to minimize
. Note that the first part doesn't depend
on y and the second part doesn't depend on
x, so we can minimize these parts separately. Here is how to minimize
 , the second part is minimized similarly. As the expression in the brackets doesn't
depend on j, this part can be rewritten as
, the second part is minimized similarly. As the expression in the brackets doesn't
depend on j, this part can be rewritten as
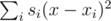 , where
, where
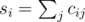 . Now it's enough to calculate the required value for all possible values of
x and choose x for which this value is the smallest. The optimal value of
y can be found similarly.
. Now it's enough to calculate the required value for all possible values of
x and choose x for which this value is the smallest. The optimal value of
y can be found similarly.
The overall complexity of this solution is O(n·m + n2 + m2).
As the objective function is convex, other approaches to this problem are possible, for example, ternary search, gradient descent or analytical approach (calculation of derivatives).
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cmath>
#include <cstring>
using namespace std;
#define N 1010
const long long inf=1LL<<60;
int n,m,a[N][N];
long long dx[N],dy[N];
int main()
{
scanf("%d%d",&n,&m);
memset(dx,0,sizeof(dx));
memset(dy,0,sizeof(dy));
for(int i=0;i<n;i++)
{
for(int j=0;j<m;j++)
{
scanf("%d",&a[i][j]);
dx[i]+=a[i][j];
dy[j]+=a[i][j];
}
}
long long mx=inf,my=inf;
int nx,ny;
for(int i=0;i<=n;i++)
{
long long ans=0;
for(int j=0;j<n;j++)
{
ans+=(4*i-4*j-2)*(4*i-4*j-2)*dx[j];
}
if(ans<mx)
{mx=ans;nx=i;}
}
for(int i=0;i<=m;i++)
{
long long ans=0;
for(int j=0;j<m;j++)
{
ans+=(4*i-4*j-2)*(4*i-4*j-2)*dy[j];
}
if(ans<my)
{my=ans;ny=i;}
}
printf("%I64d\n",mx+my);
printf("%d %d\n",nx,ny);
return 0;
}





 本文介绍了一种通过独立最小化矩阵中特定表达式的算法,该算法能够有效地找到使矩阵方差达到最小值的参数x和y。文章详细阐述了算法的原理,并提供了一个具体的实现示例。
本文介绍了一种通过独立最小化矩阵中特定表达式的算法,该算法能够有效地找到使矩阵方差达到最小值的参数x和y。文章详细阐述了算法的原理,并提供了一个具体的实现示例。
















 17万+
17万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








