Leetcode 5. Longest Palindromic Substring

最新推荐文章于 2022-10-24 21:03:12 发布

原创最新推荐文章于 2022-10-24 21:03:12 发布 · 891 阅读

0 ·

CC 4.0 BY-SA版权

算法专栏收录该内容

62 篇文章

订阅专栏

本文介绍了两种有效的算法来寻找给定字符串中的最长回文子串。第一种方法通过逐步减少子串长度来查找，第二种方法则从每个字符为中心向两边扩散以找到所有可能的回文子串。

题目：

Given a string s, find the longest palindromic substring in s. You may assume that the maximum length of s is 1000.

Example 1:

Input: "babad"
Output: "bab"
Note: "aba" is also a valid answer.

Example 2:

Input: "cbbd"
Output: "bb"

题意：

给定一个字符串，寻找字符串中最大的回文子串，可能有多个，输出一个即可。

解法：

解法一：由最长串开始寻找，逐次减一（效率不高）

一开始的想法是从最长串的开始寻找，先检查最大串是否为回文串，是的话直接返回，如果不是，长度减一，试验每一种可能，没找到，长度再减一，直到找到为止

代码：

class Solution {
    public String longestPalindrome(String s) {
        int len=s.length();
        int size=len;
        int start=0;
        while(size>=1){
            start=0;
            while((start+size)<=len){
                if(IsPalin(s.substring(start,start+size))==true) return s.substring(start,start+size);
                start++;
            }
            size--;
        }
        return "";
    }
    public boolean IsPalin(String sub){
        char[] arr = sub.toCharArray();
        int len=sub.length()/2;
        int i=0;
        int j=sub.length()-1;
        while(i<len){
            if(arr[i]!=arr[j]) return false;
            j--;
            i++;
        }
        return true;
    }
}

解法二：每个点中心发散查找

我们对子串中的每个点，由内向外扩，如果两边的字符相等，就继续外扩，直到找到最大。

对于奇数长度的回文子串

我们外扩的中心点为单点

如图：

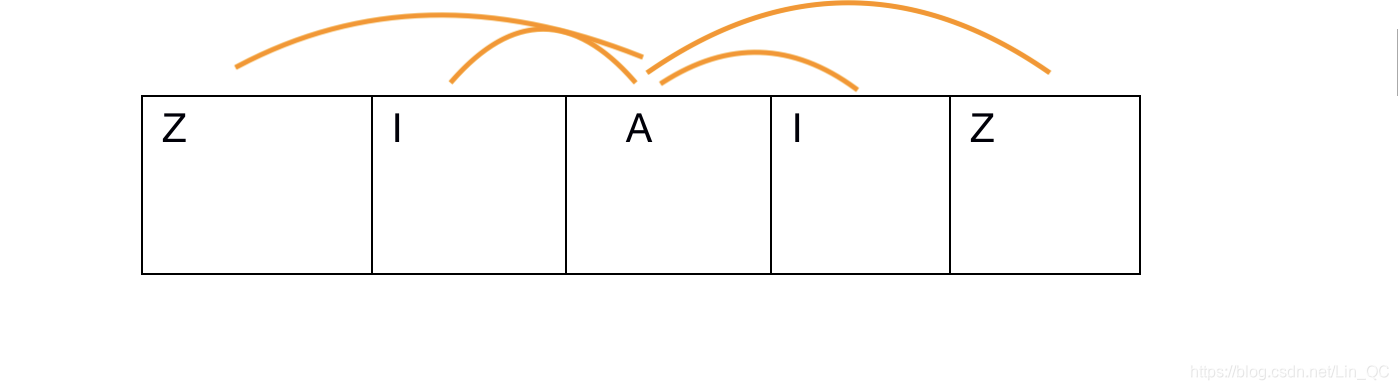
对于偶数长度中心点为对称的两点：

如图：

每个点执行后，我们只需要保存最大的那个子串即可。

代码：

class Solution {
    private int lo, maxLen;

    public String longestPalindrome(String s) {
        int len = s.length();
        if (len < 2)
            return s;

        for (int i = 0; i < len-1; i++) {
            extendPalindrome(s, i, i);  //assume odd length, try to extend Palindrome as possible
            extendPalindrome(s, i, i+1); //assume even length.
        }
        return s.substring(lo, lo + maxLen);
    }

    private void extendPalindrome(String s, int j, int k) {
        while (j >= 0 && k < s.length() && s.charAt(j) == s.charAt(k)) {
            j--;
            k++;
        }
        if (maxLen < k - j - 1) {
            lo = j + 1;
            maxLen = k - j - 1;
        }
    }
}