博弈论-第一章概述

原创已于 2022-03-27 01:05:01 修改 · 7.3k 阅读

22 ·

CC 4.0 BY-SA版权

文章标签：

#其他

于 2022-03-24 01:21:47 首次发布

博弈论-学习笔记专栏收录该内容

2 篇文章

订阅专栏

博弈论是研究决策者如何在互动环境中选择策略的理论。文章介绍了博弈的基本概念，如何定义博弈、参与者、信息和策略，并通过简单的数字游戏解释了博弈的互动性和策略选择的重要性。同时，讨论了不同类型的博弈，如合作与非合作、静态与动态、完全信息与不完全信息博弈。文中举例展示了罗森塞蜈蚣博弈和数字游戏，阐述了选择正确策略和市场的重要性，以及学习博弈论的潜在收益。

1.何为博弈：

博：博览全局。

弈：对弈棋局。

博弈：指在一定的游戏规则约束下，基于直接相互作用的环境条件，各参与人依据所掌握的信息，选择各自的策略（行动），以实现利益最大化的过程。

1）首先确定谁是博弈的对手和未来的对手

2）博弈中既存在竞争关系，也存在合作关系

2.一个简单的数字游戏：

各位同学写1个介于1与100之间的自然数（整数，包括1与100）在内，然后求出所有数字的平均数，如果你写的数字最接近该平均数的二分之一，那么你将在游戏中胜出。

一般来说，能够获胜的数字取决于平均数，平均数取决于其他人写的数字，于是你就会猜测其他人写了什么数字。如果平均数是50，那么能够获胜的数字是25，如果其他人都想到了这一层，写25，那么平均数就是25，能够获胜的数字是12，如果其他人也想到了这一层……推到极致，能够获胜的数字就是1，但其实大多数人并不会想这么多层，所以其实1获胜的概率是很低的，能够获胜的数字在区间[12,25]的可能性比较大。同时，也可能存在一些不想获胜，故意捣乱的人，会写50以上的数字。

博弈就是你中有我，我中有你。由于直接相互作用（互动），每个博弈参与者的得益不仅取决于自己的策略（行动），还取决于其他参与者的策略（行动）。博弈的核心在于整体思维基础上的理性换位思考，用他人的得益去推测他人的策略（行动），从而选择最有利于自己的策略（行动）。

3.罗森塞蜈蚣博弈

两人分钱袋子里的钱。
　　一开始钱袋子里的钱有50，A的回合，A可以选择直接分钱或继续参与。如果直接分钱，A获得40，B获得10；如果继续游戏，则钱袋子里的钱翻倍。
　　此时钱袋子里的钱有100，B的回合，B选择直接分钱则A获得20，B获得80；B选择继续游戏则钱袋子里的钱翻倍。
　　此时钱袋子里的钱有200，A的回合，A选择直接分钱则A获得160，B获得40；A选择继续游戏则钱袋子里的钱翻倍。
　　此时钱袋子里的钱有400，B的回合，B选择直接分钱则A获得80，B获得320；B选择继续游戏则钱袋子里的钱翻倍。
　　此时钱袋子里的钱有800，这是最后的回合，A获得640，B获得160。

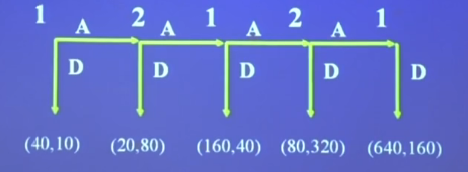
在这里插入图片描述
　　可以看出，在自己的回合中，如果选择直接分钱，自己获得的钱是对方的四倍（以第一轮为例，A获得40，B获得10），如果选择继续游戏，下一轮对方选择结束，则自己获得的钱变为原来的一半（从40变为20），而和在本轮结束相比（在第一轮结束B获得10），对方可以获得八倍报酬（B在第二轮结束可获得80）。