#include <stdio.h>
#include <windows.h>
#include "time_display.h"
static const char *cpc_s_time_weekzh[] = {"星期日", "星期一", "星期二", "星期三", "星期四", "星期五", "星期六"};
static const char *cpc_s_time_weeken[] = {"Sunday", "Monday", "Tuesday", "Wednesday", "Thursday", "Friday", "Saturday"};
static const char *cpc_s_time_weekjp[] = {"日", "月", "火", "水", "木", "金", "土"};
static const char *cpc_s_time_monthen[] = {
"January", "February", "March", "April", "May", "June",
"July", "August", "September", "October", "November", "December"
};
void v_s_time_Display_allformats(void) {
for (U1 i = 1; i <= 5; ++i) {
v_s_time_Display_format(i);
}
}
void v_s_time_Display_format(U1 u1_format_index) {
SYSTEMTIME t;
GetLocalTime(&t);
U2 y = t.wYear;
U1 m = (U1)t.wMonth, d = (U1)t.wDay;
U1 h24 = (U1)t.wHour, min = (U1)t.wMinute, sec = (U1)t.wSecond;
U1 w = (U1)t.wDayOfWeek;
U1 h12 = h24 % 12 == 0 ? 12 : h24 % 12;
const char *ampm = (h24 >= 12) ? "PM" : "AM";
switch (u1_format_index) {
case 1:
printf("格式1:%u年%u月%u日 %s %u点%u分%u秒",y, m, d, cpc_s_time_weekzh[w], h24, min, sec);
break;
case 2:
printf("格式2:%u/%u/%u %s %02u:%02u:%02u", y, m, d, cpc_s_time_weekzh[w], h24, min, sec);
break;
case 3:
printf("格式3:%u/%u/%u %s %u:%02u:%02u(%s)",y, m, d, cpc_s_time_weekzh[w], h12, min, sec, ampm);
break;
case 4:
printf("格式4:%s, %s %u, %u %02u:%02u:%02u",cpc_s_time_weeken[w], cpc_s_time_monthen[m - 1], d, y, h24, min, sec);
break;
case 5:
printf("格式5:%u年%u月%u日(%s) %u:%02u:%02u(%s)",y, m, d, cpc_s_time_weekjp[w], h12, min, sec, ampm);
break;
default:
printf("[错误] 无效格式编号:%u", u1_format_index);
break;
}
}
void v_s_time_Write_allformats_to_file(void) {
FILE *fp = fopen("time_log.txt", "a");
if (!fp) {
printf("[错误] 无法打开 time_log.txt
");
return;
}
SYSTEMTIME t;
GetLocalTime(&t);
U2 y = t.wYear;
U1 m = (U1)t.wMonth, d = (U1)t.wDay;
U1 h24 = (U1)t.wHour, min = (U1)t.wMinute, sec = (U1)t.wSecond;
U1 w = (U1)t.wDayOfWeek;
U1 h12 = h24 % 12 == 0 ? 12 : h24 % 12;
const char *ampm = (h24 >= 12) ? "PM" : "AM";
fprintf(fp, "格式1:%u年%u月%u日 %s %u点%u分%u秒",y, m, d, cpc_s_time_weekzh[w], h24, min, sec);
fprintf(fp, "格式2:%u/%u/%u %s %02u:%02u:%02u",y, m, d, cpc_s_time_weekzh[w], h24, min, sec);
fprintf(fp, "格式3:%u/%u/%u %s %u:%02u:%02u(%s)",y, m, d, cpc_s_time_weekzh[w], h12, min, sec, ampm);
fprintf(fp, "格式4:%s, %s %u, %u %02u:%02u:%02u",cpc_s_time_weeken[w], cpc_s_time_monthen[m - 1], d, y, h24, min, sec);
fprintf(fp, "格式5:%u年%u月%u日(%s) %u:%02u:%02u(%s)",y, m, d, cpc_s_time_weekjp[w], h12, min, sec, ampm);
fprintf(fp, "----------------------------------------");
fclose(fp);
}帮我完善一下
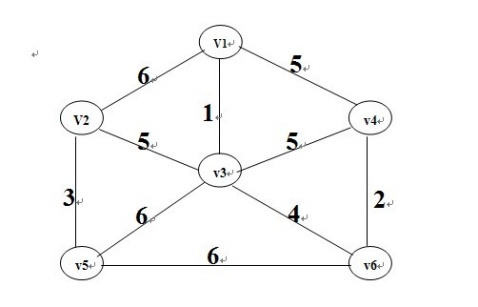





 本文详细介绍了Prim算法和Kruskal算法两种求解最小生成树的方法。Prim算法通过贪心思想逐步构建最小生成树,而Kruskal算法则是一条条边地遍历,将不属于同一连通分量的顶点通过边连接起来。文章提供了具体实现代码。
本文详细介绍了Prim算法和Kruskal算法两种求解最小生成树的方法。Prim算法通过贪心思想逐步构建最小生成树,而Kruskal算法则是一条条边地遍历,将不属于同一连通分量的顶点通过边连接起来。文章提供了具体实现代码。
















 10万+
10万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








