【学习笔记】（数学）线性代数-矩阵的概念和特殊矩阵

矩阵的相关概念

• 由 $m\times n$ 个数按一定的次序排成的 $m$ 行 $n$ 列的矩形数表成为 $m\times n$ 的矩阵，简称矩阵(matrix)。
• 横的各排称为矩阵的行，竖的各列称为矩阵的列。
• 元素为实数的称为实矩阵，一般情况下我们所讨论的矩阵均为实矩阵。
• 1 行 $n$ 列的矩阵称为行矩阵，$n$ 行 1 列的矩阵称为列矩阵。

矩阵的表示

$a_{ij}$ 表示矩阵第 $i$ 行第 $j$ 列的元素。矩阵通常用大写字母 $A,B,C$ 等表示，如下图为一般的矩阵：
$$A=\left(\begin{array}{cccc}{a}_{11}& a_{12}& \cdots & a_{1n}\\ a_{21}& a_{22}& \cdots & a_{2n}\\ a_{31}& a_{32}& \cdots & a_{3n}\\ ⋮& ⋮& \cdots & ⋮\\ a_{m1}& a_{m2}& \cdots & a_{mn}\end{array}\right)$$
还可以简记为 $A=(a_{ij}{)}_{m\times n}$.
行矩阵样例：
$$(a_{1n},a_{2n},a_{3n},\cdots ,a_{1n})$$
列矩阵样例：
$$\left(\begin{array}{c}{a}_{11}\\ a_{21}\\ a_{31}\\ ⋮\\ a_{n1}\end{array}\right)$$

特殊的矩阵形式

方阵

• 当一个矩阵的 $m=n$ ，即矩阵的行数与列数相同时，称矩阵为方阵(square matrix)。
• 贯穿 $a_{11},a_{22},a_{33},\cdots ,a_{nn}$ 的对角线称为 主对角线，主对角线的特征是行编号与列编号相等，不是方阵的矩阵不存在主对角线。
  -贯穿 $a_{1n},a_{2(n-1)},\dots ,a_{n1}$ 的对角线称为斜对角线，斜对角的特征是右上和左下的元素行列编号相反。不是方阵的矩阵不存在斜对角线。
  $$A_{n\times n}=\left(\begin{array}{ccccc}{a}_{11}& a_{12}& \cdots & a_{1(n-1)}& a_{1n}\\ a_{21}& a_{22}& \cdots & a_{2(n-1)}& a_{2n}\\ ⋮& ⋮& & ⋮& ⋮\\ a_{(n-1)1}& a_{(n-1)2}& \cdots & a_{(n-1)(n-1)}& a_{(n-1)n}\\ a_{n1}& a_{n2}& \cdots & a_{n(n-1)}& a_{nn}\end{array}\right)$$

零矩阵

元素均为 0 的方阵称为零矩阵，通常用大写字母 O 表示。反之若至少有一个非零元素的矩阵称为非零矩阵。
$$O_{mn}=\left(\begin{array}{ccc}0& \cdots & 0\\ ⋮& \ddots & ⋮\\ 0& ⋮& 0\end{array}\right)$$

对角矩阵

除一条主对角线外其他元素均为 0 的方阵称为对角矩阵。
$$\Lambda =\left(\begin{array}{ccc}{a}_{11}& & \\ & \ddots & \\ & & a_{nn}\end{array}\right)$$

单位矩阵

除一条主对角线上的元素均为 1 外，其他的元素均为 0 的方阵称为单位矩阵。
$$E_n=\left(\begin{array}{ccc}1& & \\ & \ddots & \\ & & 1\end{array}\right)$$

数量矩阵

除一条主对角线上的元素均为 $k$ 外，其他的元素均为 0 的方阵称为数量矩阵。

三角矩阵

三角阵分为上三角阵和下三角阵。上三角阵是指左下角元素均为 0 的方阵，下三角阵是指右上角元素均为 0 的方阵。
上三角阵:

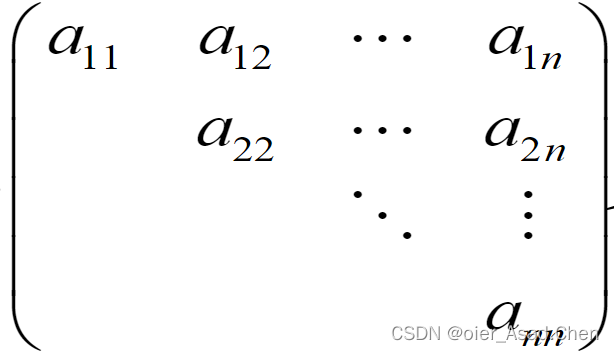
下三角阵:

梯形阵

设 $A=(a_{ij}{)}_{mn}$ 为非零矩阵，若非零行（即至少存在有一个非零元素的行）全在零行的上面，

• A中各非零行中的第一个非零元素前面零元素的个数随行数的增大而增多，则称为上梯形矩阵，如下两个样例。
  $$\left(\begin{array}{ccccc}1& 2& 3& 4& 5\\ 0& 0& 7& 8& 0\\ 0& 0& 0& 0& 0\end{array}\right)$$
  $$\left(\begin{array}{ccccc}5& 7& 0& 12& 3\\ 0& 1& 2& 2& 1\\ 0& 0& 0& 0& 1\end{array}\right)$$
• A中各非零行中的最后一个非零元素后面零元素的分数随行数的增大而减少，则称为下梯形矩阵，如下两个样例。
  $$\left(\begin{array}{ccccc}1& 0& 0& 0& 0\\ -9& 6& 0& 0& 0\\ 1& 2& 3& 0& 0\\ 5& 2& 3& 3& 0\end{array}\right)$$$$\left(\begin{array}{cccc}1& 0& 0& 0\\ 1& 2& 0& 0\\ 0& 0& 0& 0\end{array}\right)$$