特征离散化解决非线性特征问题

在实际工作中，需要使用譬如LR这种线性分类器的时候，往往需要将特征离散化成0/1特征，之后再进行模型训练。

下面举例说明原因：

我们假设决策面为y=x^2，且模型是只具有一维特征x的线性模型,即模型的表达形式为：y=kx+b，如下图所示：

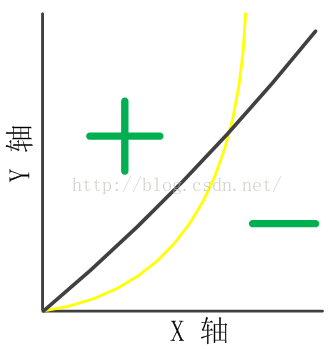
显然，模型不能很好地拟合决策面，那么，假如将x离散化成多个0/1特征(one-hot编码)：

0<x<=s1    x1=1,else=0

s1<x<=s2  x2=1,else=0

s2<x<=s3  x3=1,else=0

...

则新的模型表达形式如下：

y=k1x1+k2x2+k3x2+...+knxn+b

这时候新的决策面的表达形式为：

0<x<=s1    y=k1+b

s1<x<=s2  y=k2+b

s2<x<=s3  y=k3+b

...

那么，如下图所示：

     

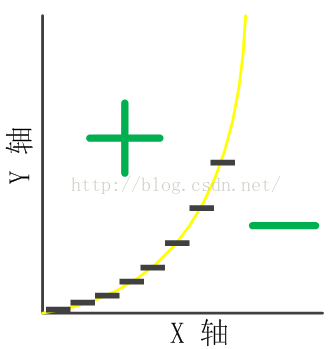
经过离散化后的特征训练出来的模型可以更好地拟合决策面。