问题:
有了一张自驾旅游路线图,你会知道城市间的高速公路长度、以及该公路要收取的过路费。现在需要你写一个程序,帮助前来咨询的游客找一条出发地和目的地之间的最短路径。如果有若干条路径都是最短的,那么需要输出最便宜的一条路径。
输入格式:
输入说明:输入数据的第1行给出4个正整数N、M、S、D,其中N(2≤N≤500)是城市的个数,顺便假设城市的编号为0~(N−1);M是高速公路的条数;S是出发地的城市编号;D是目的地的城市编号。随后的M行中,每行给出一条高速公路的信息,分别是:城市1、城市2、高速公路长度、收费额,中间用空格分开,数字均为整数且不超过500。输入保证解的存在。
输出格式:
在一行里输出路径的长度和收费总额,数字间以空格分隔,输出结尾不能有多余空格。
输入样例:
4 5 0 3
0 1 1 20
1 3 2 30
0 3 4 10
0 2 2 20
2 3 1 20
输出样例:
3 40
代码长度限制: 16 KB 内存限制:64 MB
Java (javac) 时间限制:800 ms 其它编译器时间限制:400 ms
答案:
本题主要考察有权图的单源最短路径算法。由于该题中图含有两个权重类型,并且对时间的限制比较严格,因此这里采用Dijkstra算法进行实现。
示例推演:
dist数组最终反映的是:起点到达各个点最短路径长度;
price数组最终反映的是:在最短路径长度的前提下,起点到达各个点的最少费用总额;
collect数组最终反映的是:各个顶点被收录的情况,未被收录的点即是起点无法到达的点;
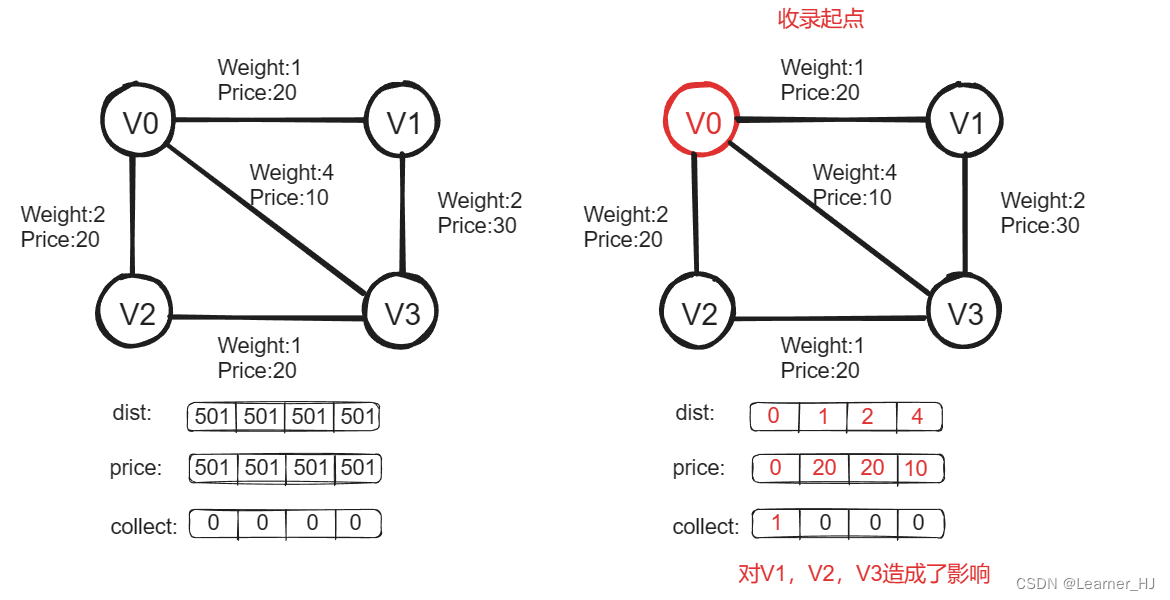
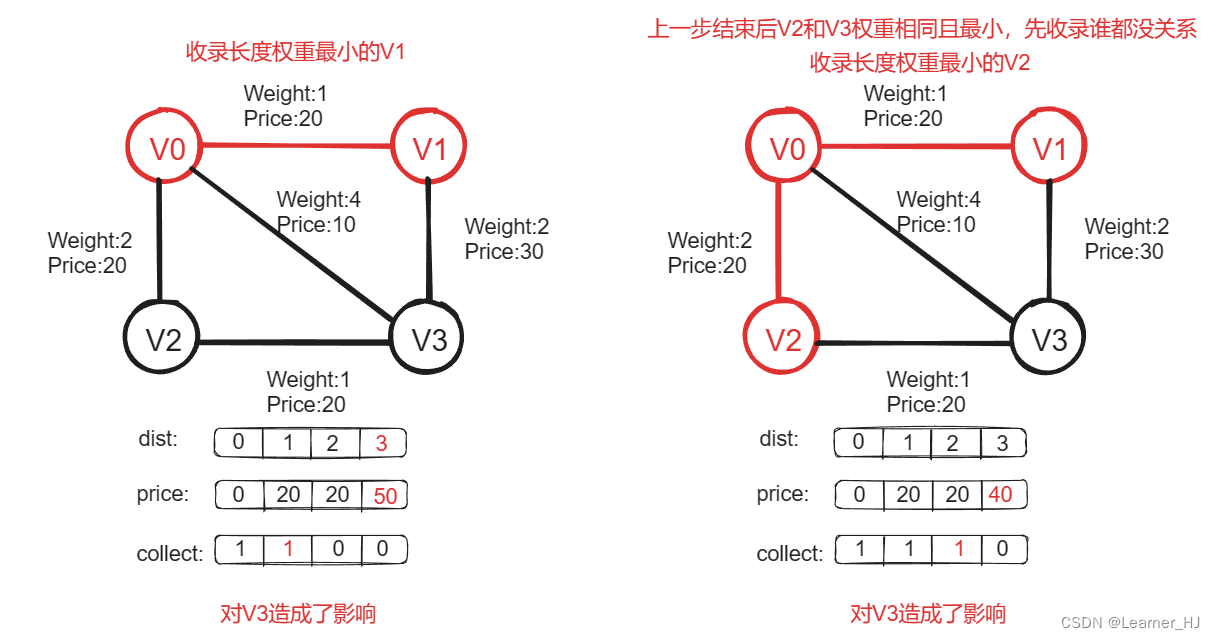
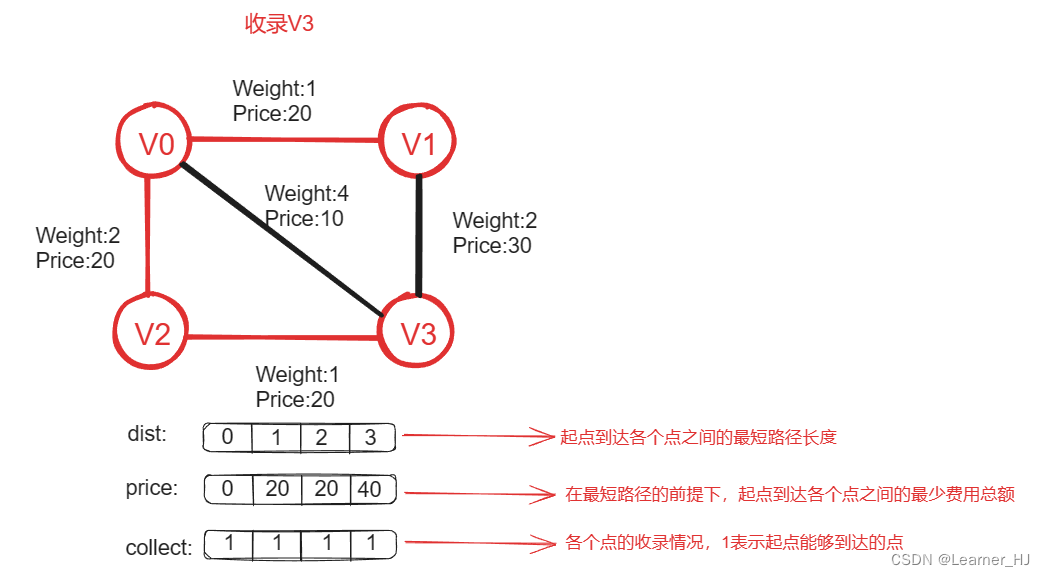
代码展示:
# include<stdio.h>
# include<stdlib.h>
# define MAXVERTEMNUM 501
# define ERROR -1
// 边结构
struct ElementType{
int Weight; // 长度
int Price; // 价格
};
// 图结构(采用邻接矩阵存储边信息)
typedef struct MGraphNode* MGraph;
struct MGraphNode{
struct ElementType Martrix[MAXVERTEMNUM][MAXVERTEMNUM];
int Nv; // 顶点数
int Ne; // 边数
};
MGraph CreateMGraph();
void InsertMGraph(MGraph Graph);
int FindMinDist(MGraph Graph, int dist[], int collected[]);
void Dijkstra(MGraph Graph, int dist[],int price[],int Start);
int main(){
// 创建一个空图
MGraph Graph = CreateMGraph();
// 接受起点和终点
int Start, End;
scanf("%d %d",&Start,&End);
// 向图中插入边
InsertMGraph(Graph);
// 执行Dijkstra算法;dist存储路径总长度,price存储收费总额
int dist[MAXVERTEMNUM], price[MAXVERTEMNUM];
Dijkstra(Graph,dist,price,Start);
// 输出结果
printf("%d %d",dist[End],price[End]);
// 释放图
free(Graph);
return 0;
}
// 返回一个空图
MGraph CreateMGraph(){
// 接收顶点和边信息
int Nv,Ne;
scanf("%d %d",&Nv,&Ne);
MGraph Graph = (MGraph)malloc(sizeof(struct MGraphNode));
Graph->Nv = Nv;
Graph->Ne = Ne;
// 元素结构中的长度和路径初始化为"正无穷"
int i,j;
for(i=0;i<Graph->Nv;i++){
for(j=0;j<Graph->Nv;j++){
struct ElementType Element = {MAXVERTEMNUM, MAXVERTEMNUM};
Graph->Martrix[i][j] = Element;
}
}
return Graph;
}
// 向图中插入边
void InsertMGraph(MGraph Graph){
int V1,V2,Weight,Price;
int i;
for(i=0;i<Graph->Ne;i++){
scanf("%d %d %d %d",&V1,&V2,&Weight,&Price);
struct ElementType Element = {Weight,Price};
// 无向图插入两次
Graph->Martrix[V1][V2] = Element;
Graph->Martrix[V2][V1] = Element;
}
return;
}
// Dijkstra算法:实时更新收录一个结点对其(未被收录的)邻接点造成的影响
void Dijkstra(MGraph Graph, int dist[],int price[],int Start){
// 记录收录情况的数组
int collected[MAXVERTEMNUM];
// 初始化路径总长度,收费总额,收录数组
int V,W;
for(V=0;V<Graph->Nv;V++){
dist[V] = Graph->Martrix[Start][V].Weight;
price[V] = Graph->Martrix[Start][V].Price;
collected[V] = 0;
}
// 收录起点
dist[Start] = 0;
price[Start] = 0;
collected[Start] = 1;
// 开始计算起点到达各个顶点的最短路径
while(1){
// V为未被录用顶点中长度权重最小者
V = FindMinDist(Graph,dist,collected);
if(V==ERROR)break;
// 收录V
collected[V] = 1;
for(W=0;W<Graph->Nv;W++){
// V的收录可能会对其未被收录的邻接结点W的权重造成影响
if(collected[W]==0 && Graph->Martrix[V][W].Weight<MAXVERTEMNUM){
// 同理:收录W的其它邻接结点也可能会对W的权重造成影响,因此要进行实时判断更新
if(dist[V]+Graph->Martrix[V][W].Weight < dist[W]){
// 选择路径最短是首要
dist[W] = dist[V] + Graph->Martrix[V][W].Weight;
price[W] = price[V] + Graph->Martrix[V][W].Price;
}else if(dist[V]+Graph->Martrix[V][W].Weight == dist[W]){
// 路径长度相同的情况下,选择费用更少的
if(price[V]+Graph->Martrix[V][W].Price < price[W]){
price[W] = price[V]+Graph->Martrix[V][W].Price;
}
}
}
}
}
// 题目保证了有解的存在,因此不需要判断所有顶点是否全部被收录
return;
}
// 返回没有被收录的顶点中dist(长度权重,因为长度权重是前提)最小者
int FindMinDist(MGraph Graph, int dist[], int collected[]){
int MinV,V;
int MinDist = MAXVERTEMNUM;
for(V=0;V<Graph->Nv;V++){
if(collected[V]==0 && dist[V]<MinDist){
MinDist = dist[V];
MinV = V;
}
}
// 顶点全部收录或者还有剩下的顶点不满足收录的要求则返回ERROR
if(MinDist<MAXVERTEMNUM)return MinV;
else return ERROR;
}
运行结果:
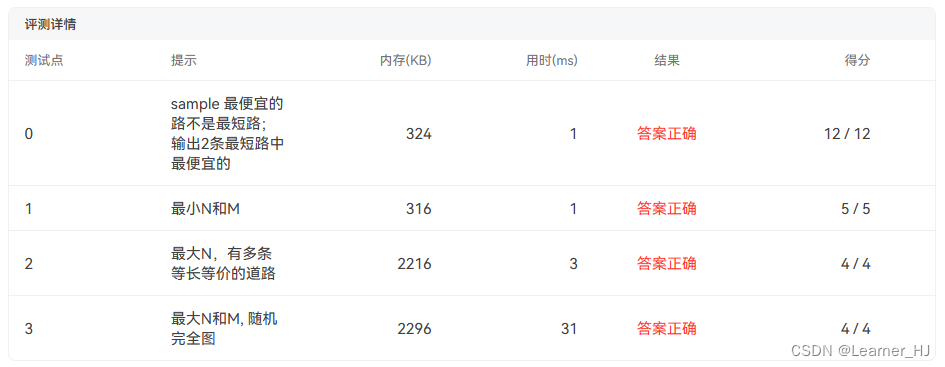




















 3660
3660

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








