初学数据结构——从零开始的数据结构学习第四天（线性表的顺序存储方式）

前言

本博客为本人在学习数据结构路途上的知识整理，如觉得对有你有所帮助，还希望留下一个赞。由于博主只是一名大一新生，如果博文中出现错误，欢迎指正。如果想要转载，附上链接就行。

注：

本文中的颜色标记

• 红色部分为重点内容
• 蓝色部分为注释

---

一、线性表的顺序存储表示

线性表的顺序表示又称为顺序存储结构或顺序映像。

定义：

把逻辑上相邻的数据元素存储在物理上相邻的存储单元中的存储结构。

•  线性表的第1个数据元素a1的存储位置，称作线性表的起始位置或基地址。
• 线形表顺序存储结构占用一片连续的存储空间。

线性表中元素存储位置的计算

假设线性表的每个元素需占x个存诸单元，则第i +1个数据元素的存储位置和第i个数据元素的存储位置之间满足关系：
LOC(ai + 1) = LOC(ai) + x
由此，所有数据元素的存储位置均可由第一个数据元素的存储位置得到：
LOC(ai) = LOC(a1) + (i - 1) * x

线性表顺序存储结构的图示

•  以物理位置相邻表示逻辑关系，任一元素均可随机存取。

顺序表的顺序存储结构实现

流程

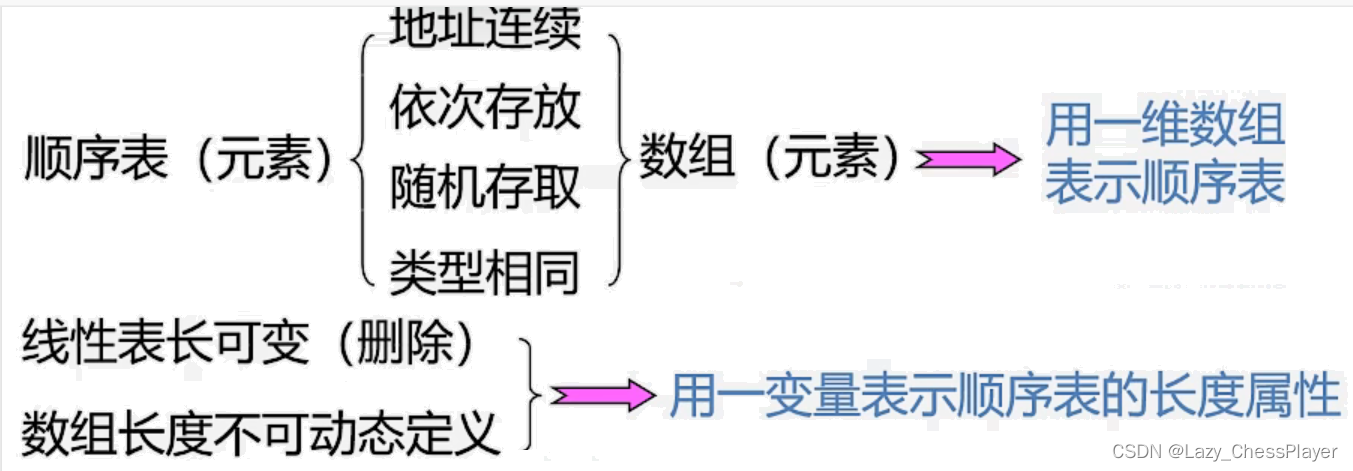
创建顺序存储结构的顺序表

#include <stdio.h>
#include <stdlib.h>
//引用头文件

typedef struct
{
    int data;
}ElemType;
//利用结构体储存数据元素，并命名为为ElemType，方便调用
//数据元素可以为任意数据类型,这里的数据元素为整形

typedef struct
{
    ElemType* elem;
//开辟数组空间
    int length;
//存储线性表的表长
} SqList;
//创建结构体，包含数据元素数组和表长。

初始化线性表

InitList(&L)

操作结果:构造一个空的线性表L。

void InitList(SqList* L)
{
    L->elem = (ElemType*)malloc(sizeof(ElemType) * MAXLENGTH);
    //利用malloc开辟一块动态的储存空间
    L->length = MAXLENGTH;
    //MAXLENGTH一般由我们自己利用宏来定义，为线性表初始表长
    assert("初始化失败" && L->elem != NULL);
    //断言开辟空间成功，失败则停止程序
}

销毁线性表

DestroyList(&L)

初始条件：线性表L已经存在。
操作结果：销毁线性表L。

void DestroyList(SqList& L)
{
    free(L.elem);
    //释放线性表的存储空间
    L.elem = NULL;
    //将指针置空
    L.length = 0;
    //将长度归零
}

重置线性表

ClearList(&L)

初始条件：线性表L已经存在。
操作结果：将线性表l重置为空表。

void ClearList(SqList& L)
{
    L.length = 0;
    //将长度归零
}

判断线性表是否为空

ListEmpty(L)

初始条件：线性表L已经存在。
操作结果：若线性表L为空表则返回TURE；否则返回FALSE。

bool ListEmpty(SqList L)
{
    if (L.length == 0)
        return true;
    else
}

获得线性表长度

ListLength(L)

初始条件：线性表L已经存在。
操作结果：返回线性表L中的数据元素个数。

int ListLength(SqList L)
{
    return L.length;
}

查找第i个元素

GetElem(L,i,&e)

初始条件：线性表L已经存在。
操作结果：用e返回线性表L中第i个数据元素的值。

bool GetElem(SqList L, int i, ElemType& e)
{
    if (i < 1 || i > L.length)
        return false;
    //判断位置是否合法
    e = *(L.elem + i - 1);
    return true;
}

查找满足一定条件的元素

LocateElem(L,e,compare())

初始条件：线性表L已经存在，compare()是数据元素判定函数。
操作结果：返回L中第1个与e满足compare()的数据元素的位序。若这样的数据元素不存在则返回值为0。

int LocateElem(SqList L, ElemType e, bool(*compare)(ElemType, ElemType))
{
    int i;
    ElemType* p = L.elem;
    //创建索引
    for (i = 1; i <= L.length; i++)
    {
        if (compare(*(p + i - 1), e))
            return i;
    }
    //枚举寻找目标元素，可以优化使用其他寻找方式
    return 0;
}

查找指定元素的前驱

PriorElem(L,cur_e,&pre_e)

初始条件：线性表L已经存在。
操作结果：若cur_e是L的数据元素,且不是第一个,则用pre_e返回它的前驱，否则操作失败；pree无意义。

// 若cur_e是L的数据元素，且不是第一个，则用pre_e返回它的前驱，否则操作失败；pre_e无意义。
bool PriorElem(SqList L, ElemType cur_e, ElemType& pre_e)
{
    int i;
    for (i = 2; i <= L.length; i++)
    {
        if ((L.elem + i - 1)->data == cur_e.data)
        {
            pre_e = *(L.elem + i - 2);
            return true;
        }
    }
    //枚举寻找cur_e
    return false;
}

查找指定元素的后继

NextElem(L, cure, &next_e)

初始条件：线性表L已经存在。
操作结果：若cur_e是L的数据元素，且不是最后个,则用next_e返回它的后继，否则操作失败，next_e无意义，

bool NextElem(SqList L, ElemType cur_e, ElemType& next_e)
{
    int i;
    for (i = 1; i <= L.length - 1; i++)
    {
        if ((L.elem + i - 1)->data == cur_e.data)
        {
            next_e = *(L.elem + i);
            return true;
        }
    }
    //枚举寻找cur_e
    return false;
}

在指定位置插入元素

Listlnsert(&L, i, e)

初始条件:线性表L已经存在，1<=i<= ListLength(L)+1。
操作结果：在L的第i个位置之前插入新的数据元素e，L的长度加一。
插入元素e之前（长度为n）：(a1,a2,...,ai-1,ai...,an)
插入元素e之后（长度为n+1）：(a1,a2,...,aj-i,e,ai, ...an)

bool ListInsert(SqList& L, int i, ElemType e)
{
    if (i < 1 || i > L.length + 1)
        return false; 
    //判断插入位置是否合法
    ElemType* q = &(L.elem[i - 1]);
    //q为插入位置
    for (ElemType* p = &(L.elem[L.length - 1]); p >= q; --p)
        *(p + 1) = *p;
    //插入位置及之后的元素右移
    *q = e;
    ++L.length; 
    //长度加1
    return true;
}

删除指定位置的元素

ListDelete(&L,i,&e)

初始条件:线性表L已经存在，1<=i<= ListLength(L)。
操作结果：删除L的第i个数据元素,并用e返回其值，L的长度减一。
删除前（长度为n）：(a1,a2,...,ai-1,ai,ai+1,...an)
删除后（长度为n-1）：(a1,a2,...,ai-1,ai+1,...,an)

bool ListDelete(SqList& L, int i, ElemType& e)
{
    if (i < 1 || i > L.length)
        return false;
    //判断删除位置是否合法
    ElemType* p = &(L.elem[i - 1]);
    //p为被删除元素的位置
    e = *p; // 被删除元素的值赋给e
    ElemType* q = L.elem + L.length - 1;
    //表尾元素位置
    for (++p; p <= q; ++p) *(p - 1) = *p;
    //被删除元素之后的元素左移
    --L.length;
    //长度减1
    return true;
}

枚举线性表中所有元素，依次调用指定操作

ListTraverse(&L,visited())

初始条件：线性表L已经存在。
操作结果：依次对线性表中每人元素调用visited().

void ListTraverse(SqList L, void(*visit)(ElemType))
{
    ElemType *p = L.elem;
    for (int i = 1; i <= L.length; ++i)
        visit(*(p++));
}

小结

线性表的特点

1. 利用数据元素的存储位置表示线性表中相邻数据元素之间的前后天系即线性表的逻辑结构与存储结构一致
2. 在访问线性表时，可以快速地计算出任何一个数据元素的存储地址因此可以粗略地认为，访问每个元素所花时间相等

• 这种存取元素的方法被称为随机存取法

顺序表的操作算法分析

• 时间复杂度

查找、插入、删除算法的平均时间复杂度为O(n）

• 空间复杂度

显然，顺序表操作算法的空间复杂度S(n)=O(1）（没有占用辅助空间）

顺序表优缺点

• 优点：

1. 存储密度大（结点本身所占存储量/结点结构所占存储量）
2. 可以随机存取表中任一元素

• 缺点：

1. 在插入、删除某一元素时，需要移动大量元素
2. 浪费存储空间
3. 属于静态存储形式，数据元素的个数不能自由扩充

注：

由于博主最近比较忙，没办法一次整理完所有知识点，可能会分比较多篇，请见谅