数据结构学习笔记——线性表逻辑结构和顺序存储结构

2.1线性表的逻辑结构

 线性表的数据元素的特点：同一数据类型

一、线性表的逻辑定义

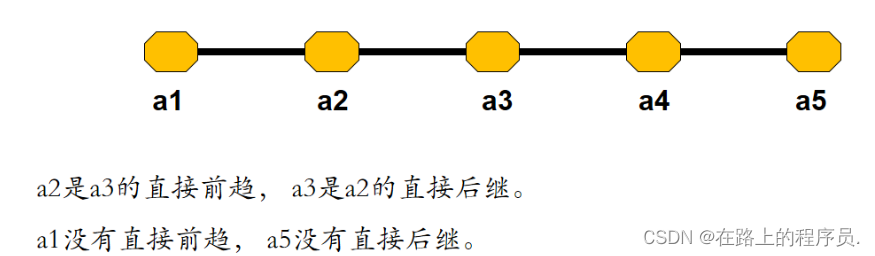
线性表是由n个数据元素（结点）a1，a2，…，an组成的有限序列。

二、线性表的基本运算

---

2.2线性表的顺序存储结构

一、顺序表定义及地址运算

1.顺序表的定义：用顺序存储方法存储的线性表。

所谓顺序存储方法存储的线性表就是把线性表的结点按逻辑次序依次存放在一组地址连续的存储单元里的方法。

2.顺序表的地址计算

 地址计算公式：LOC(ai)=LOC(a1)+(i-1)*c   (c为存储单元)

  a1为数据元素的起始地址。

3.顺序表类型定义

 typedef struct{

    int data[10];    //向量data用于存放结点

    int length;    //当前表的长度

 }SeqList;   //结构体类型

二、顺序表基本运算

1.插入运算（  O（n） ）

在线性表L中第i个数据元素之前插入数据元素x的算法如下：

步骤：1.先判断位置是否合法；2.判断线性表是否空间已满；3.移动元素；4插入元素，改变线性表长度

void InsertList(SeqList *L,DataType x,int i){

 // 将新结点x插入L所指的顺序表的第i个结点ai的位置上

int j;

if(i<1||i>L->length+1)  Error("position error"); //非法位置

if(L->length>=ListSize)   Error("overflow");   //表示空间溢出

for(j=L->length-1;j>=i-1;j--)

  L->data[j+1]=L->data[j];

  L->data[i-1]=x;

  L->Length++;

}

算法分析：

算法时间主要耗费在移动元素的操作上。

若插入在尾结点之后，则根本无需移动；若元素全部后移；若要考虑在各种位置插入（共n+1种可能）

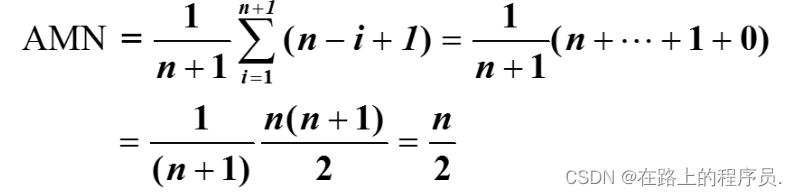
2.删除运算（将删除元素的后继一个个往前移动）

 步骤：1.判断删除位置i是否合法；2.移动结点；（将第i+1至第n位的元素依次向前移动一个位置）3.表长减1，删除成功返回OK

void DeleteList(SeqList *L,int i)

{//从L所指的顺序表中删除第i个结点ai

int j;

if(i <1 || i>L->length-1)

Error("position error");   //非法位置

for(j=i;j<=L->length-1;j++)

L->data[j-1]=L->data[j];    //结点前移

L->length--;      //表长减小

}

算法分析

算法时间主要耗费在移动元素的操作上。

1.若删除尾结点，则根本无需移动（特别快）

2.若删除首结点，则表中n-1个元素全部前移（特别慢）

3.若考虑在各种位置删除（共n种可能）的平均移动次数，该如何计算？

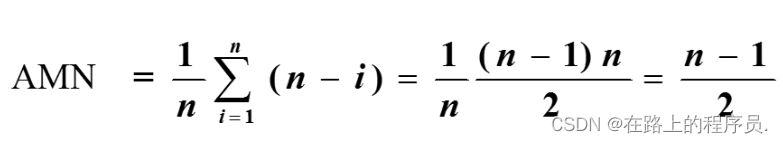
   动态数组存储线性表      申请空间完成初始化

#define MAXSIZE 100    //最大长度

typedef struct

{

    ElemType *elem;   //指向数据元素的基地

    int length；           //线性表的当前长度

}SqList;

 

顺序表基本运算（动态数组存储线性表版）

1.初始化线性表

Status InitList_Sq(Sqlist*L)

{

L->elem=(ElemType*)malloc(sizeof(ElemType)*MAXSIZE);

if(!L->elem)   exit(OVERFLOW);

L->length=0;

return OK;

}

2.获取线性表L中的第i个数据元素的内容

int LocateNode(SqList *L,int i,DataType &e)

{

if(i<1||i>L->length)     return ERROR;

//判断i值是否合理，若不合理，返回ERROR

e=L->elem[i-1];

return OK;

}

3.在线性表L中查找值为x的数据元素的位置

int LocateNode(SqList *L,ElemType x)

{

for(i=0;i<L->length;i++)

     if(L->elem[i]==x)

        return i+1;

return 0;

}

 

 补充：

• 1.利用数据元素的存储位置表示线性表中相邻数据元素之间的前后关系，即线性表的逻辑结构与存储结构一致
• 2.在访问线性表时，可以快速地计算除任何一个数据元素的存储地址。因此可以粗略的认为。访问每个元素所花时间相等。这种存取元素的方法被称为随机存取法

•  优点：1.存储密度大（结合本身所占存储量/结点结构所占存储量）；2.可以随机存取表中任一元素
•  缺点：1.在插入、删除某一元素时，需要移动大量元素；2.浪费存储空间；3.属于静态存储形式，数据元素的个数不能自由扩充。
• 逻辑结构与存储结构相同。

---