LeetCode #308 - Range Sum Query 2D - Mutable

最新推荐文章于 2023-07-22 15:47:14 发布

原创最新推荐文章于 2023-07-22 15:47:14 发布 · 276 阅读

0 ·

CC 4.0 BY-SA版权

LeetCode 专栏收录该内容

625 篇文章

订阅专栏

本文介绍了一种高效的数据结构和算法，用于处理二维矩阵的区间求和问题，并能在矩阵元素更新后快速调整求和结果。通过使用树状数组（Binary Indexed Tree），实现了O(logn)的时间复杂度进行区间求和和元素更新操作。

题目描述：

Given a 2D matrix matrix, find the sum of the elements inside the rectangle defined by its upper left corner (row1, col1) and lower right corner (row2, col2).

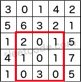
The above rectangle (with the red border) is defined by (row1, col1) = (2, 1) and (row2, col2) = (4, 3), which contains sum = 8.

Example:

Given matrix = [

[3, 0, 1, 4, 2],

[5, 6, 3, 2, 1],

[1, 2, 0, 1, 5],

[4, 1, 0, 1, 7],

[1, 0, 3, 0, 5]

]

sumRegion(2, 1, 4, 3) -> 8

update(3, 2, 2)

sumRegion(2, 1, 4, 3) -> 10

Note:

1. The matrix is only modifiable by the update function.

2. You may assume the number of calls to update and sumRegion function is distributed evenly.

3. You may assume that row1 ≤ row2 and col1 ≤ col2.

class NumMatrix {
public:
    NumMatrix(vector<vector<int>> matrix) {
        if(matrix.size()==0||matrix[0].size()==0) return;
        m=matrix;
        v=vector<vector<int>>(matrix.size()+1,vector<int>(matrix[0].size()+1,0));
        for(int i=1;i<v.size();i++)
        {
            for(int j=1;j<v[0].size();j++)
            {
                add(i,j,matrix[i-1][j-1]);
            }
        }
    }
    
    void update(int row, int col, int val) {
        add(row+1,col+1,val-m[row][col]);
        m[row][col]=val;
    }
    
    int sumRegion(int row1, int col1, int row2, int col2) {
        return sum(row2+1,col2+1)-sum(row1,col2+1)-sum(row2+1,col1)+sum(row1,col1);
    }
    
    int lowbit(int x)
    {
        return x&-x;
    }
    
    void add(int row, int col, int x)
    {
        int r=row;
        while(r<v.size())
        {
            int c=col;
            while(c<v[0].size())
            {
                v[r][c]+=x;
                c+=lowbit(c);
            }
            r+=lowbit(r);
        }
    }
    
    int sum(int row, int col)
    {
        int sum=0;
        int r=row;
        while(r>0)
        {
            int c=col;
            while(c>0)
            {
                sum+=v[r][c];
                c-=lowbit(c);
            }
            r-=lowbit(r);
        }
        return sum;
    }
    
private:
    vector<vector<int>> v; // 树状数组下标从1开始
    vector<vector<int>> m; // 原数组下标从0开始
};