Codeforces Round 1014 (Div. 2)题解

于 2025-04-08 17:54:38 发布
阅读量1.3k 收藏 28
点赞数 30
CC 4.0 BY-SA版权
分类专栏： 题解 文章标签： 算法 c++
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.youkuaiyun.com/LancyMorry/article/details/147057324

Codeforces Round 1014 Div. 2

A题（2092A） Kamilka and the Sheep

在这里插入图片描述

原题目截屏，我懒得打字儿

  • 题意：T组数据，给定n个不重复的数， a 1 , a 2 , . . . , a n {a_1,a_2,...,a_n} a1​,a2​,...,an​，然后选择一个d，然后求 g c d ( a i + d , a j + d ) gcd(a_i+d,a_j+d) gcd(ai​+d,aj​+d)的最大值

  • 思路：咋一看，可能不知道它在说什么，浅显的来讲，先看样例

    2
    1 3

    结果是2，说是选择d=1来的

    5
    5 4 3 2 1

    结果是4，选择的d是3，然后取 a 1 {a_1} a1​和 a 5 {a_5} a5​有 g c d ( 1 + 3 , 5 + 3 ) = 4 gcd(1+3,5+3)=4 gcd(1+3,5+3)=4

  • 那么观察有两个想法

    • 选取的是最大的值和最小的值，这点可以在其余样例中得到验证
    • 最终得到的gcd值就是最大值和最小值的差值m

赛场上到这里就可以直接开干了，就是这么简单
代码：

void solve() {
    int n=read();
    ll mmax=0,mmin=1e9;
    for(int i=1;i<=n;i++){
        ll x=read();
        mmax=max(mmax,x);
        mmin=min(mmin,x);
    }
    printf("%lld\n",mmax-mmin);
}
int main() {
    int t=read(); 
    while (t--) 
        solve();
    return 0;
}

我不希望我的代码可以直接被人利用.jpg

当然我们事后肯定要写一写证明，先是可行性证明:

假设 a i {a_i} ai​和 a j {a_j} aj​分别是数组内的最大最小值
m m m为差值，即 a i − a j = m {a_i-a_j}=m ai​−aj​=m，令 d = m − a j d=m-a_j d=m−aj​，能够得到
a i + d = m + a j + m − a j = 2 m a_i+d=m+a_j+m-a_j=2m ai​+d=m+aj​+m−aj​=2m
a j + d = a − j + m − a j = m a_j+d=a-j+m-a_j=m aj​+d=a−j+m−aj​=m
显然， g c d ( a i + d , a j + d ) = m gcd(a_i+d,a_j+d)=m gcd(ai​+d,aj​+d)=m

然后是正确性证明

根据上面的证明我们可知 g c d ( x + d , y + d ) gcd(x+d,y+d) gcd(x+d,y+d)的最大值就是 a b s ( x − y ) abs(x-y) abs(x−y)
所以如果我们能够证明说明 g c d ( a j + m + d , a j + d ) gcd(a_j+m+d,a_j+d) gcd(aj​+m+d,aj​+d)的最大值是 m m m
那么只需要取差值最大的两个数也就是使得m最大的两个 a i a_i ai​和 a j a_j aj​即可
我这里直接给一个最浅显的证明，就是辗转相除
g c d ( a j + m + d , a j + d ) = g c d ( a j + d , m ) gcd(a_j+m+d,a_j+d)=gcd(a_j+d,m) gcd(aj​+m+d,aj​+d)=gcd(aj​+d,m)
我们都知道 g c d ( x , y ) < = x 且 g c d ( x , y ) < = y gcd(x,y)<=x且gcd(x,y)<=y gcd(x,y)<=x且gcd(x,y)<=y
那么显然当 a j + d = m a_j+d=m aj​+d=m时 g c d ( a j + d , m ) gcd(a_j+d,m) gcd(aj​+d,m)取最大为m
很自然吧，但是需要注意的是，为什么这里能够用辗转相除
前提条件是 ( a j + m + d ) / ( a j + d ) = 1.... m (a_j+m+d)/(a_j+d)=1....m (aj​+m+d)/(aj​+d)=1....m，其中 m < a j + d m<a_j+d m<aj​+d
那么 d d d一定满足 m − a j < d m-a_j<d m−aj​<d吗？
显然不是，但是如果取 m − a j > = d m-a_j>=d m−aj​>=d，也就是 m > = a j + d m>=a_j+d m>=aj​+d
同样的由于 g c d ( x , y ) < = x 且 g c d ( x , y ) < = y gcd(x,y)<=x且gcd(x,y)<=y gcd(x,y)<=x且gcd(x,y)<=y
有 m > = a h + d > = g c d ( a j + m + d , a j + d ) m>=a_h+d>=gcd(a_j+m+d,a_j+d) m>=ah​+d>=gcd(aj​+m+d,aj​+d)
所以无论怎么取 d ， m d，m d，m都是 g c d ( a j + m + d , a j + d ) gcd(a_j+m+d,a_j+d) gcd(aj​+m+d,aj​+d)的最大值

想不到吧，所以有些时候一个看似很简单的题，赛场上只需要两三分钟就能看出来正解的题，严格的证明麻烦得要死，所以一定要区分赛场上和下来复现拆解的情况

B题（2092B） Lady Bug

在这里插入图片描述
这个题目找了vjudge上的deepseek翻译版，反正大差不差，终归还是中文好看一点的

  • 题意：T组数据，然后每组给两个01串，看能否通过斜着交换上下两串的字符，使得第一个串为全0串
    什么意思呢，就比如
    A : 010 , B : 010 ， s w a p ( a 2 , b 1 ) A:010 , B:010 ，swap(a_2,b_1) A:010,B:010，swap(a2​,b1​)以后 A : 000 , B : 110 A:000,B:110 A:000,B:110，这样就是满足题意的
  • 思路：在模拟一下这个链式的过程也就是 s w a p ( a 1 , b 2 ) , s w a p ( b 2 , a 3 ) , s w a p ( a 3 , b 4 ) swap(a_1,b_2),swap(b_2,a_3),swap(a_3,b_4) swap(a1​,b2​),swap(b2​,a3​),swap(a3​,b4​)的过程中发现
    • 其实我们可以通过类似的链式交换把 a 1 a_1 a1​换到任何 B B B中一个下标为偶数的位置
    • 推广一下， A A A中一个下标为奇数的1可以换到 B B B中任何一个下标为偶数的0
    • 类似的， A A A中下标为偶数的1可以换到 B B B中任何一个下标为奇数的0

那么其实解题思路就很简单啦， A A A中的奇数下标和 B B B中的偶数下标为一组， A A A中的偶数下标和 B B B中的奇数下标一组，分别统计两个组的1出现次数，看看B串中能不能放下这么多1(需要把第一组的1放在B的偶数位置去，第二组的1放到B的奇数位置去。)

代码：

void solve() {
    int n=read();
    string s1,s2;
    cin>>s1>>s2;
    int ct1=0,ct2=0;
    for(int i=0;i<n;i++){
        if(i%2==0){
            if(s1[i]=='1') ct1++;
            if(s2[i]=='1') ct2++;
        }
        else{
            if(s1[i]=='1') ct2++;
            if(s2[i]=='1') ct1++;
        }
    }
    if(ct1>n/2||ct2>n-n/2){
        printf("NO\n");
    }
    else printf("YES\n");
 
}
int main() {
    int t = read(); 
    while (t--) 
        solve();
    return 0;
}

C题（2092C）Asuna and the Mosquitoes

在这里插入图片描述
不得不说，还是伟大的中文看着让人亲切，但是CF比赛的时候却没有这种好事，悲（

  • 题意：T组数据，把一个数组分成奇数数组和偶数数组，然后挑一个奇数和一个偶数，可以让其中一个数+1，另一个数-1，求变换以后能够得到的最大值
  • 思路：首先还是看样例，比较仁慈
    • 需要先考虑数组中全为奇数和全为偶数的情况：直接取最大值就行了
    • 接下来就是重头戏，有奇数有偶数的情况下怎么办
      我们画一画第四个样例合并的过程，奇数数组有三个元素3，5，9，偶数数组有两个元素2，4
      • 如果说9直接把4和2都合并了，那么我们能够得到15，显然不是正确答案，那么正确答案从哪里来的呢？
      • 因为每次加减都是以1为增量的，所以我们可以控制不得到15，而选择在14停下，也就是偶数数组中留一个1，
      • 用成为偶数的14继续去合并奇数数组中的元素，14直接和5合并完又成了19，剩下三个奇数3,19,1肯定也不是最优的
      • 所以同样的思路就是合并到18的时候停下，剩下3，1，1，18四个元素，然后18和3合并，最后得到1，1，21，因此最大值为21
    • 所以我们回过头来看这个过程
      • 模拟拿最大的奇数来合并的过程，先合并偶数元素
      • 如果还有剩下的其他奇数，那么偶数就剩下一个1，保证自己是偶数，来合并剩下的奇数
      • 那么同样的道理，如果合并后还有剩下的其他奇数，是不是同样可以留下一个1，（本来偶数+奇数=奇数），来使得自己成为偶数
      • 继续这个过程，直到合并以后没有奇数剩余的情况，就不用再留下1啦
    • 那么我们动用一下聪明的脑瓜儿，剩下的1的个数是几个？
    • 提示：如果两个奇数一个偶数，需要把偶数留下1，如果三个奇数一个偶数，除了偶数留下的1，还要多留下一个奇数1
    • 是的，聪明的你一定发现了，剩下的1的个数就是奇数元素个数-1！（在既有奇数又有偶数的情况下），所以剩下的作为答案的最大值是多少茉？好难猜莉

代码：

void solve() {
    int n=read();
    int ct1=0,ct2=0;
    ll sum=0;
    int mmax=0;
    for(int i=1;i<=n;i++){
        int x=read();
        mmax=max(mmax,x);
        sum+=x;
        if(x%2==1) ct1++;
        else ct2++;
    }
    if(!ct1||!ct2){
        printf("%d\n",mmax);
    }
    else{
        ll re=sum-ct1+1;
        printf("%lld\n",re);
    }

}

int main() {
    int t = read(); 
    while (t--) 
        solve();
    return 0;
}

D题（2092D）Mishkin Energizer

在这里插入图片描述
超级模拟题，不嘻嘻

  • 题意： 给一个长度为n的字符串，然后有三种字符ABC，通过不超过2n次生成操作：AC中可以生成一个新的字符B，串就变成ABC（选取的i为1），然后让ABC三种字符的数量相等

  • 思路：还是先看样例 T I L I I TILII TILII

    • 第一步：i取1，TI中生成一个L − > T L I L I I ->TLILII −>TLILII
    • 第二步：i取2，LI中生成一个T − > T L T I L I I ->TLTILII −>TLTILII
    • 第三步：i取3，TI中生成一个L − > T L T L I L I I ->TLTLILII −>TLTLILII
    • 第四步：i取4，LI中生成一个T − > T L T L T I L I I ->TLTLTILII −>TLTLTILII

    呃，其实没看出啥，但是我自己通过瞎画，倒是发现了无论怎样的情况，只要能执行生成操作，好像都能够减少三种字符的相对相对差值

  • 比如在AB的情况下多生成1个A,最开始AB各一个，A和B相对差值为0，A和C相对差值为1,
    生成过后的ABACAB中A三个，B两个，C一个，A和B相对差值为1，A和C相对差值为2
    于是就等效于多生成了一个A

void A_B_add_A(int pos,char A,char B,char C){
    ans.push_back(pos);     // ACB
    mo.insert(mo.begin()+pos,C);
    ans.push_back(pos+1);   // ACAB
    mo.insert(mo.begin()+pos+1,A);
    ans.push_back(pos);     // ABCAB
    mo.insert(mo.begin()+pos,B);
    ans.push_back(pos+1);   // ABACAB
    mo.insert(mo.begin()+pos+1,A);
}
  • 同理，在AB的情况下多生成1个B
void A_B_add_B(int pos,char A,char B,char C){
    ans.push_back(pos);     //ACB
    mo.insert(mo.begin()+pos,C);
    ans.push_back(pos);     //ABCB
    mo.insert(mo.begin()+pos,B);
    ans.push_back(pos+1);   //ABACB
    mo.insert(mo.begin()+pos+1,A);
    ans.push_back(pos+2);   //ABABCB
    mo.insert(mo.begin()+pos+2,B);
}
  • 最简单的，在AB的情况下生成一个C
void A_B_add_C(int pos,char A,char B,char C){    
    ans.push_back(pos);     //ACB
    mo.insert(mo.begin()+pos,C);
}

  • 因为这三种操作的存在，所以可以保证无论是怎样的序列，只要有两种以上的字符我们就可以通过变魔术，来补三种字符间的相对差值（没有严格证明一定少于2*n哈，算的时候记录一下，别真超过了）

  • 有人看到这三种操作就要开始了，有必要这么麻烦吗？我可以直接想样例中一样，差哪一个字符，就在另外两个字符间执行一次生成操作不就行了嘛？

  • 你说的对，但是假如是AABCC的情况，需要你生成一个B呢？所以这种情况下就会需要用到我提到的1、2中算法

  • 但是如果都采用1和2这种操作，我估计是一定会超过2n次的，那么所以我们需要先考虑第三种情况，能用3操作的情况下先用3，用不了3再考虑1,2的情况

  • 因为数据范围很小，所以可以每次生成操作以后再次统计各个字符的数量，找到最少的那个，也就是需要生成的那个，然后先看能不能用3生成，用不了3再用1和2

代码：

vector<int> ans;
vector<char> mo;
void A_B_add_A(int pos,char A,char B,char C){
    ans.push_back(pos);     // ACB
    mo.insert(mo.begin()+pos,C);
    ans.push_back(pos+1);   // ACAB
    mo.insert(mo.begin()+pos+1,A);
    ans.push_back(pos);     // ABCAB
    mo.insert(mo.begin()+pos,B);
    ans.push_back(pos+1);   // ABACAB
    mo.insert(mo.begin()+pos+1,A);
}
void A_B_add_B(int pos,char A,char B,char C){
    ans.push_back(pos);     //ACB
    mo.insert(mo.begin()+pos,C);
    ans.push_back(pos);     //ABCB
    mo.insert(mo.begin()+pos,B);
    ans.push_back(pos+1);   //ABACB
    mo.insert(mo.begin()+pos+1,A);
    ans.push_back(pos+2);   //ABABCB
    mo.insert(mo.begin()+pos+2,B);
}
void A_B_add_C(int pos,char A,char B,char C){    
    ans.push_back(pos);     //ACB
    mo.insert(mo.begin()+pos,C);
}
char s[330];
void solve() {
    mo.clear();
    ans.clear();
    int n=read();
    int ct1=0,ct2=0,ct3=0;
    for(int i=1;i<=n;i++){
        cin>>s[i];
        if(s[i]=='T') ct1++;
        else if(s[i]=='L') ct2++;
        else ct3++;
        mo.push_back(s[i]);
    }
    char A,B,C;
    if(n==ct1||n==ct2||n==ct3){
        printf("-1\n");
    }
    else{
        if(ct1==ct2&&ct2==ct3){
            printf("0\n");
            return;
        }
        bool f=0;
        int cnt=0;
        while(1){
            bool f1=0,f2=0;
            cnt++;
            // printf("Before step %d, the string is :",cnt);
            // for(int i=0;i<mo.size();i++) cout<<mo[i];
            // cout<<endl;

            if(ct1<=ct2&&ct1<=ct3){
                for(int i=0;i<mo.size()-1;i++){
                    if(mo[i]=='L'&&mo[i+1]=='I'||mo[i]=='I'&&mo[i+1]=='L'){
                        A_B_add_C(i+1,mo[i],mo[i+1],'T');
                        f1=1;
                        break;
                    }
                }
                if(!f1){
                    for(int i=0;i<mo.size()-1;i++){
                        if(mo[i]=='L'&&mo[i+1]=='T'){
                            A_B_add_B(i+1,mo[i],'T','I');
                            f2=1;
                            break;
                        }
                        if(mo[i]=='I'&&mo[i+1]=='T'){
                            A_B_add_B(i+1,mo[i],'T','L');
                            f2=1;
                            break;
                        }
                        if(mo[i]=='T'&&mo[i+1]=='L'){
                            A_B_add_A(i+1,'T','L','I');
                            f2=1;
                            break;
                        }
                        if(mo[i]=='T'&&mo[i+1]=='I'){
                            A_B_add_A(i+1,'T','I','L');
                            f2=1;
                            break;
                        }
                    }
                }
            }
            else if(ct2<=ct1&&ct2<=ct3){
                for(int i=0;i<mo.size()-1;i++){
                    if(mo[i]=='T'&&mo[i+1]=='I'||mo[i]=='I'&&mo[i+1]=='T'){
                        A_B_add_C(i+1,mo[i],mo[i+1],'L');
                        f1=1;
                        break;
                    }
                }
                if(!f1){
                    for(int i=0;i<mo.size()-1;i++){
                        if(mo[i]=='T'&&mo[i+1]=='L'){
                            A_B_add_B(i+1,mo[i],'L','I');
                            f2=1;
                            break;
                        }
                        if(mo[i]=='I'&&mo[i+1]=='L'){
                            A_B_add_B(i+1,mo[i],'L','T');
                            f2=1;
                            break;
                        }
                        if(mo[i]=='L'&&mo[i+1]=='T'){
                            A_B_add_A(i+1,'L','T','I');
                            f2=1;
                            break;
                        }
                        if(mo[i]=='L'&&mo[i+1]=='I'){
                            A_B_add_A(i+1,'L','I','T');
                            f2=1;
                            break;
                        }
                    }
                }
            }
            else{
                for(int i=0;i<mo.size()-1;i++){
                    if(mo[i]=='T'&&mo[i+1]=='L'||mo[i]=='L'&&mo[i+1]=='T'){
                        A_B_add_C(i+1,mo[i],mo[i+1],'I');
                        f1=1;
                        break;
                    }
                }
                if(!f1){
                    for(int i=0;i<mo.size()-1;i++){
                        if(mo[i]=='L'&&mo[i+1]=='I'){
                            A_B_add_B(i+1,'L','I','T');
                            f2=1;
                            break;
                        }
                        if(mo[i]=='T'&&mo[i+1]=='I'){
                            A_B_add_B(i+1,'T','I','L');
                            f2=1;
                            break;
                        }
                        if(mo[i]=='I'&&mo[i+1]=='L'){
                            A_B_add_A(i+1,'I','L','T');
                            f2=1;
                            break;
                        }
                        if(mo[i]=='I'&&mo[i+1]=='T'){
                            A_B_add_A(i+1,'I','T','L');
                            f2=1;
                            break;
                        }
                    }
                }
            }
            if(!f1&&!f2) break;
            ct1=0,ct2=0,ct3=0;
            for(int i=0;i<mo.size();i++){
                if(mo[i]=='T') ct1++;
                else if(mo[i]=='L') ct2++;
                else ct3++;
            }

            // printf("After this step, the string is :");
            // for(int i=0;i<mo.size();i++) cout<<mo[i]; 
            // cout<<endl;

            if(ct1==ct2&&ct2==ct3) {
                f=1;
                break;
            }
        }
        if(f==0||ans.size()>2*n){
            printf("-1\n");
        }
        else{
            printf("%d\n",ans.size());
            for(int i=0;i<ans.size();i++)
                printf("%d\n",ans[i]);
        }
    }
}

int main() {
    int t = read(); 
    while (t--) 
        solve();
    return 0;
}

我写的是纯纯模拟，所以看起来很冗余，但是其实就是复制粘贴，稍作修改，我不会把这个集成化（哭）

附上官方题解代码：

#include <algorithm>
#include <iostream>
#include <vector>
 
using namespace std;
 
signed main() {
    ios_base::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr);
    string base = "LIT";
    int t; cin >> t;
    while (t--) {
        int n; string s;
        cin >> n >> s;
        if (count(s.begin(), s.end(), s[0]) == n) {
            cout << -1 << '\n';
        } else {
            vector <int> ans;
            while (true) {
                vector <pair<int, char>> cnt;
                for (auto i : base) cnt.push_back(make_pair(count(s.begin(), s.end(), i), i));
                sort(cnt.begin(), cnt.end());
                if (cnt[0].first == cnt[1].first && cnt[1].first == cnt[2].first) break;
 
                auto op = [&] (int i) -> void {
                    string z = base; z.erase(find(z.begin(), z.end(), s[i])); z.erase(find(z.begin(), z.end(), s[i + 1]));
                    ans.push_back(i);
                    s = s.substr(0, i + 1) + z[0] + s.substr(i + 1);
                };
 
                bool done = false;
                for (int i = 0; i < s.size() - 1; ++i) {
                    if (s[i] == s[i + 1]) continue;
                    if (s[i] != cnt[0].second && s[i + 1] != cnt[0].second) {
                        op(i); 
                        done = true;
                        break;
                    }
                }
                
                if (done) continue;
                
                for (int i = 0; i < s.size() - 1; ++i) {
                    if (s[i] == s[i + 1]) continue;
                    if (s[i] == cnt[2].second) {
                        op(i); op(i + 1); op(i); op(i + 2); break;
                    } else if (s[i + 1] == cnt[2].second) {
                        op(i); op(i); op(i + 1); op(i + 3); break;
                    }
                }
            }
            
            cout << ans.size() << '\n';
            for (auto i : ans) cout << i + 1 << '\n';
        }
    }
}

可以看到，官方写的还是优雅啊，模拟是真的我写不了一点，呜呜呜
如果说你认真看，其实思路是一样的，因为只需要输出插入点i的次序，所以我写的哪些基本上都是多余的
但是我写的代码可以更直观地模拟生成新串的过程（绝对不是因为拿不准所以过于谨慎）

E题（2092E）She knows…

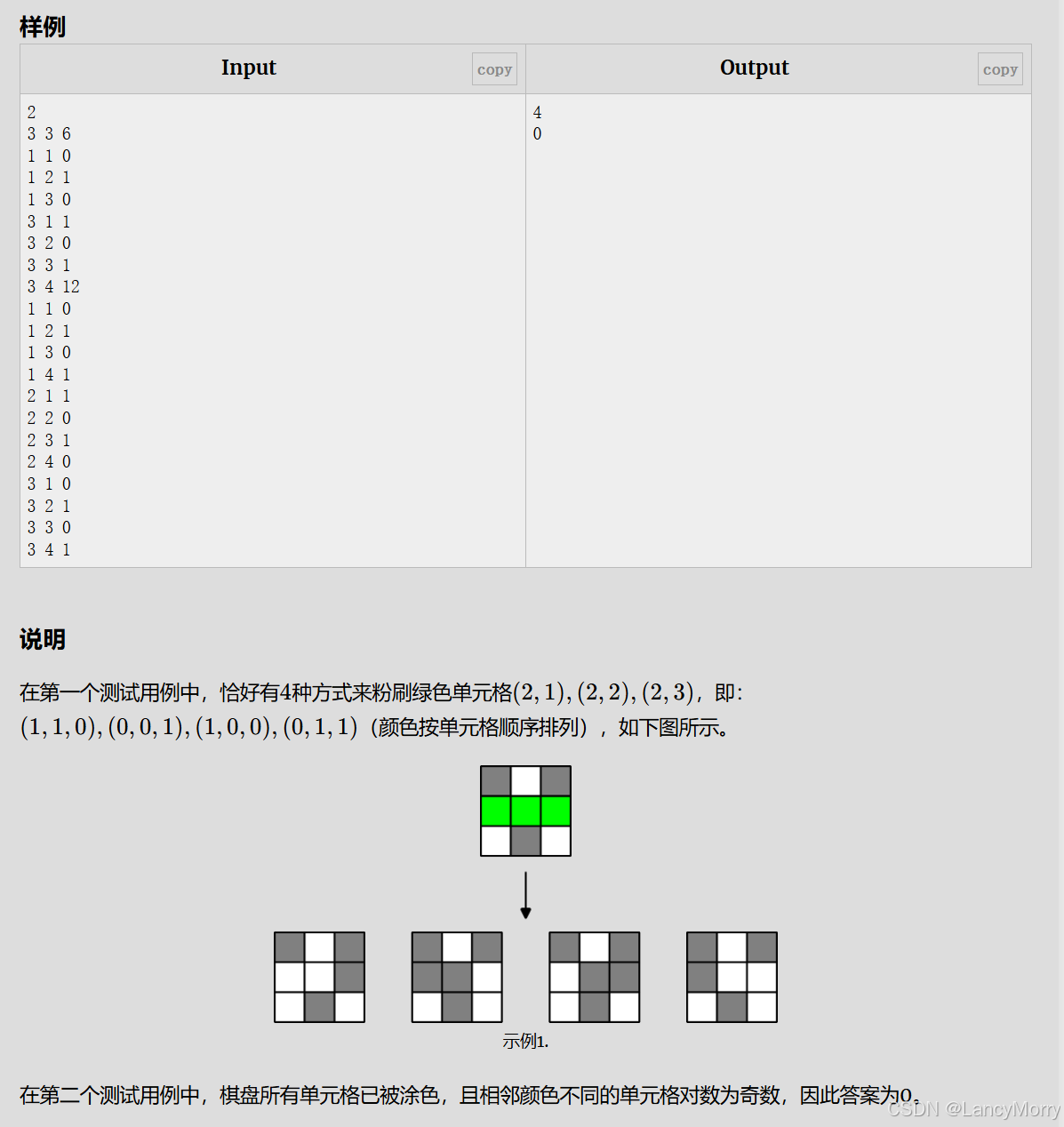
在这里插入图片描述
在这里插入图片描述
这个题看着可太抽象莉，我第一眼是没看出来到底是怎么来的
其实比赛当时没看这个题，我写D题的大模拟都没写完（真的不是因为洗澡去了迟到的问题）

  • 题意：有n*m个块，其中一些块已经上色了，一些块没有上色，问的是能够满足相邻块颜色不同的对数量为偶数的未上色块的涂色方案有多少个，结果模1e9+7
    • 初看天都塌了？这方案数咋模1e9+7？样例也看不出个啥名堂啊，但是你先别慌，根据方案数这种题的一般规律，肯定会有等价的问题
    • 结论1：四个角的块颜色黑白并不影响不同对数量的奇偶性，假设为黑，如果旁边两块为白，提供了两对颜色不同对，那么假如它翻转为白的时候，变成提供了零对颜色不同对，总和的奇偶性是不变的（本质上因为它只影响两对是否不同，只有三种情况0->2,1->1,2->0所以奇偶性维持不变）
    • 结论2：不处于边缘块的块（第2行到第n-1行，第2列到第m-1列）也不影响不同对数量的奇偶性，结论1的推广（翻转颜色只有0->4,1->3,2->2,3->1,4->0几种情况，奇偶性仍然保持不变）
    • 结论3：基于上述两个结论，我们可以知道不同对数量的奇偶性只与剩下的块有关，因为边缘上且不位于角落的块相接的对为3，翻转的情况会变成0->3,1->2,2->1,3->0几种情况，奇偶性均发生了变化
    • 因为结论1和结论2中的块不影响最后的奇偶性，假设这些块中为染色的块有k个，我们可以知道方案数至少有 2 k {2^k} 2k种，所以模数1e9+7就显得合理起来了
    • 那么剩下的，结论3中的块到底如何影响我们最后不同对数量的奇偶性呢？
    • 既然结论1和结论2存在，那么我们直接假定1和2中的块全为白色
      • 先让3中所有的块都为白色，不同对数量为0，为偶数；
      • 其中1个块为黑色，不同对数量为3，为奇数，
      • 其中2个块为黑色，不论怎么枚举，数量要么为4，要么为6，为偶数（在1个块的基础上要么+1，相邻，要么+3，不相邻）
      • 其中3个块为黑色，三块相邻：5，两块相邻，一块不相邻：7，三块均不相邻：9（本质上可以看做递归回2块黑色：要么为7，要么为9（新黑色块与k=2不相邻），要么为5，要么为7）
      • 那么到这一步，数学归纳法，该是你表演的时候啦！
    • 结论4：不同对数量的奇偶性只与3中的块有关，而且，其中黑色块为奇数时，不同对数量总和为奇数，黑色块为偶数时，不同对数量总和为偶数。
  • 接下来就是总结啦，但是其实也没那么好总结，慢慢来
    • 我们记3中的块，即位于边缘又不位于角落的块为集合S
    • 若S中所有块都已经上色了
      • 若黑色块数量为奇数，那么无论怎么刷都不满足条件,答案为0
      • 若黑色块数量为偶数，那么剩下的块随笔怎么刷都满足条件，刷了k个，还剩 n ∗ m − k n*m-k n∗m−k个没刷，答案就是 2 ( n ∗ m − k ) {2^ {(n*m-k)}} 2(n∗m−k)
    • 若S中有块没有上色，那么我们已知在S中的块里，黑色块和白色块的奇偶性相等而且奇偶各占一半（慢慢理解，就是说最终有奇数个黑色块和最终有偶数块的概率应该是相等的，因为剩下的块都有1/2的概率刷黑色，1/2刷白色），所以总方案数是 2 ( n ∗ m − k ) {2^ {(n*m-k)}} 2(n∗m−k)，其中不同对数量总和为偶数（S块中黑色块为偶数）的情况占一半，即 2 ( n ∗ m − k − 1 ) {2^ {(n*m-k-1)}} 2(n∗m−k−1)

这么看下来是不是也挺简单莉？嘻嘻
代码：

void solve(){
    int n=read(),m=read(),k=read();
    int ct=0,black_ct=0;
    for(int i=1;i<=k;i++){
        int x=read(),y=read(),c=read();
        if((x==1||x==n)&&(y!=1&&y!=m)||(y==1||y==m)&&(x!=1&&x!=n)){
            if(c==1) black_ct++;
            ct++;
        }
    }
    // printf("ct: %d, black_ct: %d\n",ct,black_ct);
    if(ct==2*m+2*n-8){
        if(black_ct%2==0)
                printf("%lld\n",qpow(1LL*n*m-k));
        else    printf("0\n");
    }
    else{
        // printf("exp: %lld\n",1LL*n*m-k-1);
        printf("%lld\n",qpow(1LL*n*m-k-1));
    }
}
int main() {
    int t=read();
    while(t--)
        solve();
    return 0;
}

F题（2092F）Andryusha and CCB

在这里插入图片描述
在这里插入图片描述
不得不说，这个题才是真抽象莉，我反正到最后都没有在看题解前把代码写出来茉
前面的都讲得比较细，这个题我自己也没写出来，所以我就写得抽象一点，建议看不懂的就不要强求了莉

  • 题意：对于一个字符串S，长度为l，对于每个子串，找到切割成k段美丽值相等的字段的k的数量，美丽值是串中0和1的交替次数
  • 思路：
    • 对于每个前缀子串长度 i i i，去考虑 k k k是比较痛苦的，因为通过样例可以发现, i i i和 i + 1 i+1 i+1的 k k k的集合关系不大
    • 所以我们要考虑一下对于 k k k来说，情况是否有变化，虽然在样例中对于 k k k来说， i i i是连续的，但是大家很容易想到,其实对于 k k k而言， i i i不一定连续，比如10111101， k k k=2的情况， i i i显然不连续
    • 那么什么是连续的呢，假设 k k k个子段中每个子段美丽值为 k i k_i ki​，那么对于 ( k i , k ) (k_i,k) (ki​,k)而言， i i i是不是一定连续了？
    • 接下来找到 ( k i , k ) (k_i,k) (ki​,k)到 ( k i , k + 1 ) (k_i,k+1) (ki​,k+1)的关系就可以破局了
    • 结论1：01串的字符可以分为两类，连续的0或1以及单独的0或1
      在这里插入图片描述
      不想写啦，给大家伙粘贴一个图片，具体实现细节还是很折磨人的

代码（官方给的std）：

#include <iostream>
#include <vector>
 
using namespace std;
 
using ll = long long;
 
void solve() {
    int n; cin >> n;
    string s; cin >> s;
    vector <int> a;
    int curr = 0;
    for (int i = 0; i < n; ++i) {
        if (i && s[i] != s[i - 1]) {
            if (curr) a.push_back(curr);
            curr = 1;
        }
        else ++curr;
    }
    a.push_back(curr);
    int sz = a.size();
 
    vector <int> ans(n, 0), left(sz, 0), right(sz, 0);
    for (int i = 0; i < sz; ++i) {
        if (!i) {
            left[i] = 0; right[i] = a[i] - 1;
        } else {
            left[i] = right[i - 1] + 1;
            right[i] = left[i] + a[i] - 1;
        }
    }
    for (int i = 0; i < sz; ++i) {
        for (int j = left[i]; j <= right[i]; ++j) {
            ans[j] += j - i + 1;
        }
    }
    vector <int> add(sz, 0);
    for (int m = 1; m < sz; ++m) {
        ll l = m, r = m, k = 1;
        while (l < sz) {
            ++add[l];
            if (r + 1 < sz) --add[r + 1];
 
            if (a[l] == 1) {
                l += m + 1;
            } else {
                l += m;
            }
 
            r += m + 1;
            ++k;
        }
    }
    int pref = 0;
    for (int i = 0; i < sz; ++i) {
        pref += add[i];
        for (int j = left[i]; j <= right[i]; ++j) {
            ans[j] += pref;
        }
    }
    for (int i = 0; i < n; ++i) {
        cout << ans[i];
        if (i != n - 1) cout << ' ';
    }
    cout << '\n';
}
 
signed main() {
    ios_base::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr);
    int t; cin >> t;
    while (t--) {
        solve();
    }
}

这是茉莉第一次写博客莉，如果写得不好或者有什么建议的地方欢迎大家指正莉，谢谢大家莉

评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值