OneDNN GEMM(AVX FP32)算法浅析

深度神经网络模型包含的计算密集型算子一般为Dense、MatMul以及Conv。对于推理引擎，其执行Dense以及MatMul算子时，一般都会调用该引擎的GEMM或者GEMV（BatchSize等于1）实现；执行Conv算子时，虽然推理引擎一般存在更好的策略，如Winograd、NCHWxC等，但大多数推理引擎也会提供GEMM策略并在一定条件下选择并执行。当卷积核各个维度的尺寸都为1时，Conv算子的执行可直接调用GEMM，当卷积核尺寸不为1时，也可以通过Im2Col将输入进行变换后，再调用GEMM获取算子的输出结果。可以认为，GEMM的执行速度将直接影响以上计算密集型算子，特别是Dense以及MatMul算子的推理效率。

OneDNN作为Intel提供的算子加速库，在x86平台上具有非常优秀的性能。一款推理引擎，如果想要在x86平台有所作为，那么OneDNN一定是其参考并且benchmark比较的对象。对于GEMM，OneDNN会根据当前运行时设备最高支持的指令集，以及算子在MNK三个维度的大小，选择不同的实现，其所设计的情况非常庞大且复杂。本文将会对OneDNN GEMM算法在FP32 AVX2指令集下的一个比较通用的分支进行描述，其代码实现详见代码文件([1])。

在以下描述中，输入A矩阵的两个维度分别为M、K，B矩阵的两个维度分别为K、N，输出C矩阵的两个维度分别为M、N。

Micro Kernel

OneDNN在AVX2指令集下采用了A(16, 8) * B(8, 6) = C(16, 6)的Micro Kernel，其计算思路如下图所示（图有点抽象）：

整个Micro Kernel的计算步骤如下：

1. 首先通过vmovups指令将A矩阵的第一列移动到两个YMM寄存器中（这里假设为YMM0以及YMM1）；

2. 随后，对于B矩阵第一行的第一个元素，使用vbroadcastss指令进行广播并存储到一个YMM寄存器内（这里假设为YMM2），然后使用fma指令vfmadd231ps将YMM0和YMM1内的元素与YMM2内元素对应相乘，并将结果累加到C矩阵的两个YMM寄存器内，这里假设为YMM4以及YMM5；

3. 沿着B矩阵第一行进行循环，重复步骤2，B矩阵广播当前行内其它数据时重复使用YMM2寄存器，并将计算结果依次累加到YMM6~YMM15寄存器内；

4. A矩阵前进一列，B矩阵前进一行，并重复步骤1~3，最终完成整个C(16, 6)矩阵的计算。

总的JIT汇编循环

OneDNN总的JIT汇编代码描述了GEMM最内层的6层循环，这里将其称为汇编Kernel，其伪代码可如下所示：

// here, m_block=16, n_block=6, k_block=8
loop with m_block in M:
  loop with n_block in N:
    loop with k_block in K:
      micro_kernel()
    save_result()

• 对于第三层对K的循环，当其完成并进行save_result时，汇编Kernel完成了一个A(16, K) * B(K, 6) = C(16, 6)的全部计算，并获得了一个分块C(16, 6)的结果；

• 对于第二层对N的循环，当其完成时，汇编Kernel获得了一个A(16, K) * B(K, N) = C(16, N)的结果，即C矩阵的某16行；

• 对于第一层对M的循环，当其完成时，汇编Kernel获得了一个A(M, K) * B(K, N) = C(M, N)的结果，即完成了当前全部的C矩阵计算。

由于输入M、N、K的任意性，很可能存在一些维度无法被其分块所整除的情况。这里分别进行讨论：

• K无法被8整除的情况

对于K无法被整除的情况，OneDNN的应对策略为生成多个不同K维度的Micro Kernel，其具体效果可如下伪代码所示（省略了许多跳转和判断细节，下同）：

loop with m_block in M:
  loop with n_block in N:
    loop with k_block in K:
      micro_kernel_k8()
    micro_kernel_k4()  // call one or zero times
    micro_kernel_k2()  // call one or zero times
    micro_kernel_k1()  // call one or zero times
    save_result()

当K无法被8整除时，其会依次判断剩余k值是否大于4、2、1并调用相应Micro Kernel进行最后的计算（如剩余5，将调用4、1一次，2零次）。

• N无法被6整除的情况

对于N无法被6整除的情况，OneDNN的应对策略与K相似，继续生成对应维度循环的汇编代码，其具体效果可如下伪代码所示：

loop with m_block in M:
  loop with n_block in N:
    loop with k_block in K:
      micro_kernel_n6k8()
    micro_kernel_n6k4()  // call one or zero times
    micro_kernel_n6k2()  // call one or zero times
    micro_kernel_n6k1()  // call one or zero times
    save_result()
  // deal with remain n
  if remain_n == 5:
    loop with k_block in K:
      micro_kernel_n5k8()
    micro_kernel_n5k4()
    micro_kernel_n5k2()
    micro_kernel_n5k1()
    save_result()
  if remain_n == 4:
    loop with k_block in K:
      micro_kernel_n4k8()
    micro_kernel_n4k4()
    micro_kernel_n4k2()
    micro_kernel_n4k1()
    save_result()
  ...
  if remain_n == 1:
    loop with k_block in K:
      micro_kernel_n1k8()
    micro_kernel_n1k4()
    micro_kernel_n1k2()
    micro_kernel_n1k1()
    save_result()

• M无法被16整除的情况

对于M无法被16整除的情况，其处理相比于K、N要更复杂一些。当剩余M不为8时，直接使用vmovups加载A矩阵数据将会造成错误加载后续数据以及数组访问越界两个问题，以上两个问题在存储C矩阵时同样存在。针对这一情况，OneDNN在加载A矩阵以及存储C矩阵时采用了mask系列指令，同时通过使用mask，当M无法被16整除时，其剩余维度的处理就可以分为三个分支了：9<=M<=15（Micro Kernel中使用一条vmovups指令以及一条vmaskmovps指令移动数据），M=8（Micro Kernel中使用一条vmovups指令移动数据）以及1<=M<=7（Micro Kernel中使用一条vmaskmovps指令移动数据）。

最终，整个汇编Kernel的伪代码将如下所示：

loop with m_block in M:
  loop with n_block in N:
    loop with k_block in K:
      micro_kernel_no_mask_m16n6k8()
    micro_kernel_no_mask_m16n6k4()  // call one or zero times
    micro_kernel_no_mask_m16n6k2()  // call one or zero times
    micro_kernel_no_mask_m16n6k1()  // call one or zero times
    save_result()
  // deal with remain n
  ...

if 9 <= remain_m <= 15:
  loop with n_block in N:
    loop with k_block in K:
      micro_kernel_with_mask_m9to15n6k8()
    micro_kernel_with_mask_m9to15n6k4()
    micro_kernel_with_mask_m9to15n6k2()
    micro_kernel_with_mask_m9to15n6k1()
    save_result()
  // deal with remain n
  ...

if remain_m == 8:
  loop with n_block in N:
    loop with k_block in K:
      micro_kernel_no_mask_m8n6k8()
    micro_kernel_no_mask_m8n6k4()
    micro_kernel_no_mask_m8n6k2()
    micro_kernel_no_mask_m8n6k1()
    save_result()
  // deal with remain n
  ...

if 1 <= remain_m <= 7:
  loop with n_block in N:
    loop with k_block in K:
      micro_kernel_with_mask_m1to7n6k8()
    micro_kernel_with_mask_m1to7n6k4()
    micro_kernel_with_mask_m1to7n6k2()
    micro_kernel_with_mask_m1to7n6k1()
    save_result()
  // deal with remain n
  ...

Pack And Copy Strategy

对于Micro Kernel，其要求A矩阵的元素必须按列存储在内存中。但A矩阵的元素可以按行来进行存储。OneDNN对于上述情况对A矩阵进行了Pack操作。以上操作在使A矩阵满足计算要求的同时，其最主要的贡献还是在计算过程中对于A矩阵的加载能够获得更好的局部性，并能够充分利用CPU的硬件Prefetch能力以减少访存带来的fma流水线气泡。

在对A矩阵进行Pack时，OneDNN没有直接开辟一个M*K*sizeof(float)字节的内存空间。在汇编Kernel循环中，注意到对于M的循环是在最外侧的，因此这里只需要开辟一个16*K*sizeof(float)的内存空间即可。在每一次M循环的起始，OneDNN对当前使用的A(16, K)进行一次Pack操作，随后便可以一直使用直到下一次的M循环。

以上Pack操作可如下图所示：

Pack

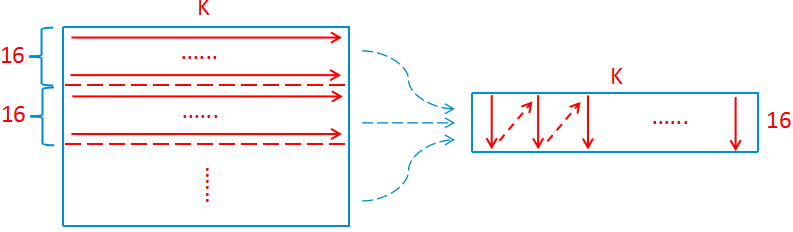
当A矩阵已经是按列存储的情况下，还需要进行Pack操作吗？答案是需要的，因为Pack操作能够加速GEMM计算过程。OneDNN把A矩阵按列存储下的Pack称为Copy操作，其实现是非常有意思的。在计算第一个A(16, K) * B(K, 6) = C(16, 6)的block时，OneDNN每一次都在读取A矩阵数据至YMM0以及YMM1寄存器的同时，将数据又拷贝至内存空间的对应位置，这一过程可以同时使用软件Prefetch指令进行加速。随后，在计算C矩阵当前16行的剩余列时，则不再从A矩阵读取数据，而是从内存空间中读取。

这里存在一个问题，如果N的值过小，例如6，那么在计算了一个C(16, 6)之后，我们下一次计算的将会是C矩阵下一个16行的6列元素，即拷贝过程变成了完全的无用功。OneDNN在这里进行了一个判断并设置了一个阈值18，即当N的值小于等于18时，其认为拷贝A矩阵带来的开销会大于随后使用A矩阵时加载连续内存空间带来的收益，不会执行拷贝操作；当N大于18时，其才会使用上述策略。

总循环

最后再来看一下总的循环，其伪代码如下所示：

loop with k_outer_block in K:
  loop with m_outer_block in M:
    loop with n_outer_block in N:
      assembly_kernel()

总的循环非常简单，就是循环K、M、N三个维度，并调用上面我们JIT产生的汇编Kernel。这里值得注意的有两个方面，一个是外层循环的顺序，使用了K、M、N；另一个则是三个外层循环分块数的取值。

一般来说，我们希望汇编Kernel进行计算的过程中，其当前处理的A、B、C三个矩阵块都至少能够保存在L2 Cache中，以加速循环计算。因此，以上三个分块的大小与当前运行环境的L2 Cache尺寸是密切相关的，一个好的做法是通过系统调用获取当前运行环境的L2 Cache尺寸，并通过经验公式进行计算获得比较理想的分块值。OneDNN没有采用上述方法，其将分块值直接进行了固定，对于N的分块，如果A矩阵转置，其取值为96，否则为48；对于K的分块，如果B矩阵转置，其取值为96，否则为256；对于M的分块，其直接固定为4032。

总结

本文对OneDNN GEMM(AVX FP32)的算法流程进行了描述，其中省略了一些细节，如果大家感兴趣，推荐结合上文的源码链接阅读本文。同时如果大家对本文有其它想法，也希望能够积极留言，讨论交流。

欢迎加入Adlik交流群、关注Adlik仓库~

Adlik微信交流群

Adlik Github仓库

[1]https://github.com/oneapi-src/oneDNN/blob/v2.6/src/cpu/x64/gemm/f32/jit_avx_gemm_f32.cpp