Dijkstra算法详解-优快云博客

dijstra

dijstra只能遍历没有负边的图

知道做noip初赛题我才真正知道原因：原因
迪杰斯特拉算法是基于贪心的算法，是图论中的基本算法
实际上我是习惯写spfa，早就知道spfa会被卡，以前我偏不信这个忠告
但经历了多次的超时后，我终于开始认真学dijstra了

dijstra算法实际上是贪心
每次从队首选出一个dis[u]最小的值，将它做标记，使它不能再被遍历
并从它开始遍历，遍历到不在队列里的点就加入队列
重复上述操作
直到队列为空

数据图
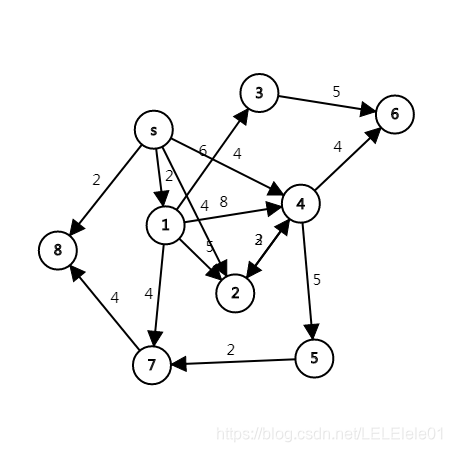
先从起点开始遍历，
初始值dis[s]=0
选出s开始遍历
每条出边到达的点进行更新，没有入队列的点入队列
第一次s便利到8，1，4，2
然后发现dis[8]或dis[2]最短，
选dis[2]或dis[8]进行更新

dijstra中的vis并不是判重标记，不可以在被更新，要和spfa有所区别

为什么上述贪心方法是对的呢？
因为所有边都是非负整数边，即后面加入队列的点不可能小于所以前面加入队列的点，
（因为后面的点是从其中一个前面的点更新而得来的，所以被更新的点一定小于等于更新它的点）
所以每次的最小的点的值不可能小于之后更新而得此点而得的值，标记，

每次选出最小的点可以由STL中的大根堆转换成小根堆实现

例题

弱化版

#include<bits/stdc++.h>
using namespace std;

const int N=10010,M=500100;
struct node{
	int w,id;
	bool operator <(const node&x)const{
	    return w>x.w;
	}
};
struct edge{
	int link,v,w,u;
}q[M*2];
int head[N],cnt=0,n,m,s;
void put(int x,int y,int z){q[++cnt].w=z;q[cnt].v=y;q[cnt].u=x;q[cnt].link=head[x];head[x]=cnt;}
priority_queue <node> myline;
bool vis[N];
int dis[N];
void dijstra(){
	for(int i=1;i<=n;i++) vis[i]=0,dis[i]=INT_MAX;
	dis[s]=0;
	myline.push((node){0,s});
	while(!myline.empty()){
		node kk=myline.top();myline.pop();
		int u=kk.id;
		if(vis[u]) continue;
		vis[u]=1;
		for(int i=head[u];i;i=q[i].link){
			int v=q[i].v;
			if(dis[v]>=dis[u]+q[i].w){
				dis[v]=dis[u]+q[i].w;
				if(!vis[v]){
				myline.push((node){dis[v],v});
			   }
	 	   } 
		}
	}
}
int main(){
	scanf("%d%d%d",&n,&m,&s);
	for(int i=1;i<=m;i++){
		int u,v,w;
		scanf("%d%d%d",&u,&v,&w);
		put(u,v,w);
	}
	dijstra();
	for(int i=1;i<=n;i++){
		printf("%d ",dis[i]);
	}
}

专卡spfa
P.S注意第二题的n数据范围，我以为是一样的结果卡炸了

#include<bits/stdc++.h>
using namespace std;

const int N=100010,M=500100;
struct node{
	int w,id;
	bool operator <(const node&x)const{
	    return w>x.w;
	}
};
struct edge{
	int link,v,w,u;
}q[M*2];
int head[N],cnt=0,n,m,s;
void put(int x,int y,int z){q[++cnt].w=z;q[cnt].v=y;q[cnt].u=x;q[cnt].link=head[x];head[x]=cnt;}
priority_queue <node> myline;
bool vis[N];
int dis[N];
void dijstra(){
	for(int i=1;i<=n;i++) vis[i]=0,dis[i]=INT_MAX;
	dis[s]=0;
	myline.push((node){0,s});
	while(!myline.empty()){
		node kk=myline.top();myline.pop();//
		int u=kk.id;
		if(vis[u]) continue;
		vis[u]=1;
		for(int i=head[u];i;i=q[i].link){
			int v=q[i].v;
			if(dis[v]>=dis[u]+q[i].w){
				dis[v]=dis[u]+q[i].w;
				if(!vis[v]){
				myline.push((node){dis[v],v});
			   }
	 	   } 
		}
	}
}
int main(){
	scanf("%d%d%d",&n,&m,&s);
	for(int i=1;i<=m;i++){
		int u,v,w;
		scanf("%d%d%d",&u,&v,&w);
		put(u,v,w);
	}
	dijstra();
	for(int i=1;i<=n;i++){
		printf("%d ",dis[i]);
	}
}