15743 兔兔与蛋蛋游戏

最新推荐文章于 2026-01-02 23:51:50 发布

原创最新推荐文章于 2026-01-02 23:51:50 发布 · 607 阅读

14 ·

CC 4.0 BY-SA版权

文章标签：

#游戏 #c++

描述

这些天，兔兔和蛋蛋喜欢上了一种新的棋类游戏。

这个游戏是在一个 n 行 m 列的棋盘上进行的。游戏开始之前，棋盘上有一个格子是空的，其它的格子中都放置了一枚棋子，棋子或者是黑色，或者是白色。

每一局游戏总是兔兔先操作，之后双方轮流操作，具体操作为：

兔兔每次操作时，选择一枚与空格相邻的白色棋子，将它移进空格。
蛋蛋每次操作时，选择一枚与空格相邻的黑色棋子，将它移进空格。

第一个不能按照规则操作的人输掉游戏。为了描述方便，下面将操作“将第x行第y列中的棋子移进空格中”记为 M(x,y)。

例如下面是三个游戏的例子。

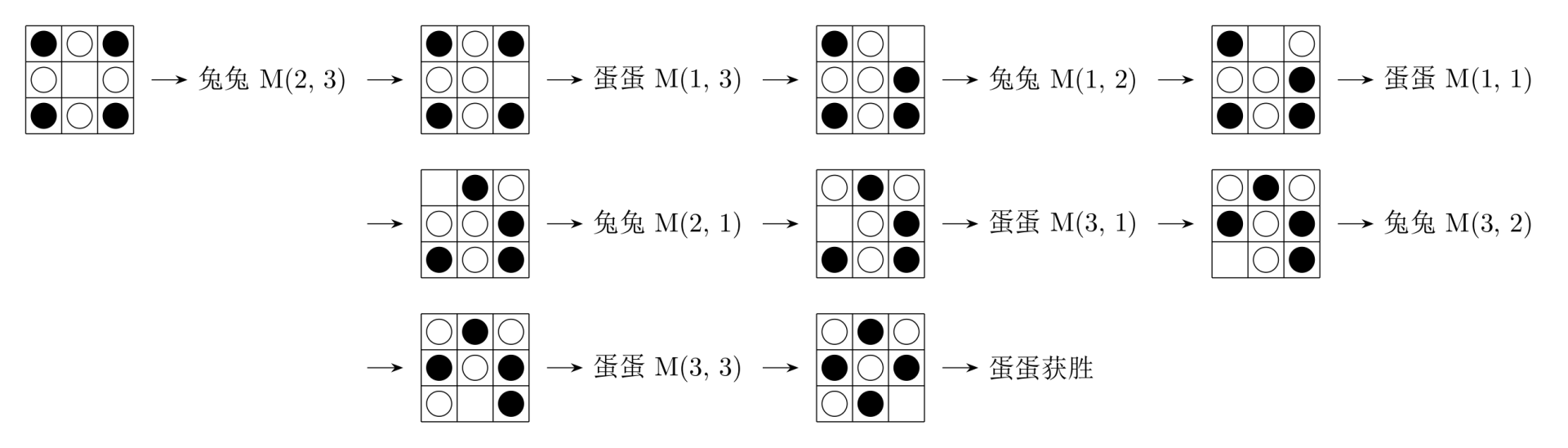
最近兔兔总是输掉游戏，而且蛋蛋格外嚣张，于是兔兔想请她的好朋友——你——来帮助她。她带来了一局输给蛋蛋的游戏的实录，请你指出这一局游戏中所有她“犯错误”的地方。

注意：

两个格子相邻当且仅当它们有一条公共边。
兔兔的操作是“犯错误”的，当且仅当，在这次操作前兔兔有必胜策略，而这次操作后蛋蛋有必胜策略。

输入描述

输入的第一行包含两个正整数 n,m。

接下来 n 行描述初始棋盘。其中第 i 行包含 m 个字符，每个字符都是大写英文字母 X、大写英文字母 O 或点号 . 之一，分别表示对应的棋盘格中有黑色棋子、有白色棋子和没有棋子。其中点号 . 恰好出现一次。

接下来一行包含一个整数 k（1≤k≤1000），表示兔兔和蛋蛋各进行了 k 次操作。

接下来 2k 行描述一局游戏的过程。其中第 2i−1 行是兔兔的第 i 次操作（编号为 i 的操作），第 2i 行是蛋蛋的第 i 次操作。每个操作使用两个整数 x,y 来描述，表示将第 x 行第 y 列中的棋子移进空格中。

输入保证整个棋盘中只有一个格子没有棋子，游戏过程中兔兔和蛋蛋的每个操作都是合法的，且最后蛋蛋获胜。

输出描述

输出文件的第一行包含一个整数 r，表示兔兔犯错误的总次数。

接下来 r 行按递增的顺序给出兔兔“犯错误”的操作编号。其中第 i 行包含一个整数 ai 表示兔兔第 i 个犯错误的操作是他在游戏中的第 ai 次操作。

样例输入 1

1 6 
XO.OXO 
1 
1 2 
1 1

样例输出 1

1
1

样例输入 2

样例输出 2

样例输入 3

4 4 
OOXX 
OXXO 
OO.O 
XXXO 
2 
3 2 
2 2 
1 2 
1 3

样例输出 3

2
1
2

提示

数据范围与提示

对于 100% 的数据，1≤n≤40，1≤m≤40，1≤k≤1000。

测试点编号	n	m
1,2	n=1	1≤m≤20
3	n=3	m=4
4,5	n=4	m=4
6,7	n=4	m=5
8	n=3	m=7
9∼14	n=2	1≤m≤40
15,16	1≤n≤16	1≤m≤16
17∼20	1≤n≤40	1≤m≤40

#include <bits/stdc++.h>
using namespace std;
const int N = 4005;
int n, m, k, cnt = 0, fir[N], nxt[N << 1], to[N << 1], vis[N], cxy[N], nx = 0, p[N][N], sx, sy, cans = 0, ans[N], win[N], del[N];
char a[N][N];
void ade(int u, int v) {
    cnt++, nxt[cnt] = fir[u], fir[u] = cnt, to[cnt] = v;
    cnt++, nxt[cnt] = fir[v], fir[v] = cnt, to[cnt] = u;
}
int dfs(int r) {
    vis[r] = 1;
    for (int i = fir[r]; i; i = nxt[i])
        if (!vis[to[i]] && !del[to[i]]) {//需判断邻接点是否被删除
            vis[to[i]] = 1;
            if (!cxy[to[i]] || dfs(cxy[to[i]])) {
                cxy[cxy[r]] = 0, cxy[to[i]] = r, cxy[r] = to[i];
                return 1;
            }
        }
    return 0;
}
void match() {
    for (int i = 1; i <= nx; i++)
        if (!cxy[i])
            memset(vis, 0, sizeof(vis)), dfs(i);
}
void getp() {
    int tmp = 0;
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= m; j++)
            if (a[i][j] == 'O')
                p[i][j] = ++tmp;
    nx = tmp;
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= m; j++)
            if (a[i][j] == 'X') p[i][j] = ++tmp;
            else if (a[i][j] == '.') p[i][j] = ++tmp, sx = i, sy = j;
}
int dx[5] = {0, 1, 0, -1};
int dy[5] = {1, 0, -1, 0};
void edge(int x, int y) {
    for (int i = 0; i < 4; i++) {
        int xx = x + dx[i], yy = y + dy[i];
        if (xx >= 1 && xx <= n && yy >= 1 && yy <= m && p[xx][yy] > nx) ade(p[x][y], p[xx][yy]);
    }
}
int main() {
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; i++) scanf("%s", a[i] + 1);
    getp();//重新标号，白点标 1~nx，剩下的 nx+1~n 依次标号
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= m; j++)
            if (a[i][j] == 'O')
                edge(i, j);//建图
    match();//先来一发最大匹配
    scanf("%d", &k);
    for (int t = 1; t <= k * 2; t++) {
        int x = p[sx][sy];
        scanf("%d%d", &sx, &sy);//注意要在continue前输入
        del[x] = 1;//直接删除
        if (!cxy[x]) continue;
        int tmp = cxy[x];
        cxy[x] = cxy[tmp] = 0, memset(vis, 0, sizeof(vis));
        if (!dfs(tmp)) win[t] = 1;//当前状态下（未操作）先手必胜
    }
    for (int i = 2; i <= k * 2; i += 2)
        if (win[i] == 1 && win[i - 1] == 1)
            ans[++cans] = i / 2;
    printf("%d\n", cans);
    for (int i = 1; i <= cans; i++) printf("%d\n", ans[i]);
    return 0;
}