C语言-汉诺塔问题

汉诺塔问题：

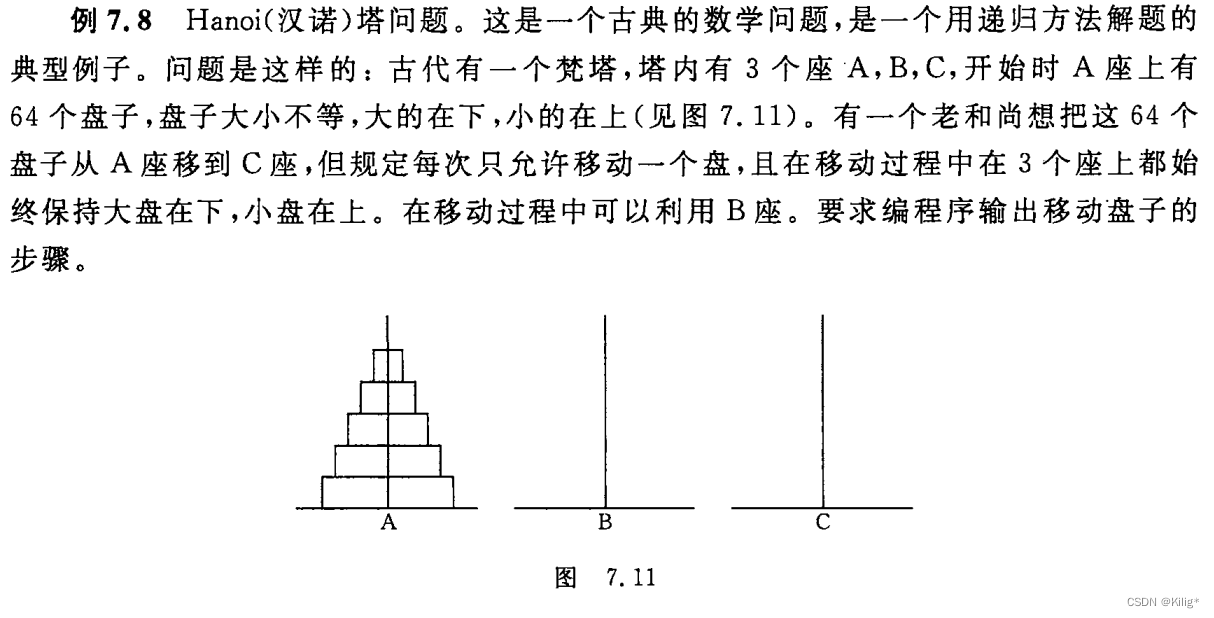
解题思路:

利用递归的思想，共64个盘子，假设有一个“超能和尚”，他能够将上面的n个盘子保持下大上小的顺序从一个柱子移到另一个柱子。那么步骤如下:

1. 超能和尚将63个盘子从A移到B。
2. 普通和尚将1个最下面的盘子从A移到C。
3. 超能和尚将63个盘子从B移到C。
   这样即可解决问题。

那么，超能和尚如何将63个盘子从A移动到B呢？也就是最开始问题的步骤1。参考上一个问题的思想。

1. 超能和尚将62个盘子从A移到C。
2. 普通和尚将1个（A的倒数第二个）盘子从A移到B。
3. 超能和尚将62个盘子从C移动到B。

同理，如何将63个盘子从B移到C呢？这也是最开始问题步骤3。同样的思想（此时经过步骤2之后C中有一个最大的盘子）

1. 超能和尚将62个盘子从B移动到A。
2. 普通和尚将1个盘子从B移动到A。
3. 超能和尚将62个盘子从A移动到C。
   这样就完成了移动。

因此，这是一个不断递归的问题（移动63个盘子->移动62个盘子->移动61个盘子->…->移动1个盘子）

因此总结规律，将n个盘子从A移到C需要经过以下步骤。

1. 超能和尚将n-1个盘子从A移动到B（借助C）。
2. 普通和尚将1个剩下的盘子从A移动到C。
3. 超能和尚将n-1个盘子从B移动到C（借助A）。

最终一个盘子的移动就交给普通和尚来完成。下面代码实现。

递归的精妙之处就是可以将问题拆解，不用考虑那么多步，找出第n-1到第n步的规律。其他的步骤交给递归调用即可。

#include <cstdio>

//假设左中右三个塔分别为A、B、C

void move_one(char begin_tower,char end_tower){
    //普通和尚的功能，实现将一个盘子从指定位置移动到指定位置
    printf("%c ---> %c\n",begin_tower,end_tower);
}

void move_many(char one,char two,char three,int n){
    //超能和尚的功能，实现将n个盘子从指定位置移动到指定位置
    //从one移到three，借助two
    if(n==1){
        //只需要移动一个盘子，调用小和尚，就不用超能和尚了
        move_one(one,three);
    }else{
        //需要移动多个盘子
        move_many(one,three,two,n-1);
        //超能和尚将n-1个盘子从A移动到B（借助C）
        move_one(one,three);
        //小和尚从A到C
        move_many(two,one,three,n-1);
    }

}

int main(){
    int n;
    printf("请输入盘子总个数");
    scanf("%d",&n);
    move_many('A','B','C',n);
    return 0;
}

题目参考《c程序设计（第四版）》-谭浩强