视频讲解:Bilibili视频详解(推荐)
目录
Transformer中多头注意力机制(Attention Is All You Need)
张量:logits 和 weights(形状均为 [b,h,n,m],m=n)
张量:Pq,Pk,Pv,Po(形状 [h,d,k] 或 [h,d,v])
Transformer中多头注意力机制(Attention Is All You Need)
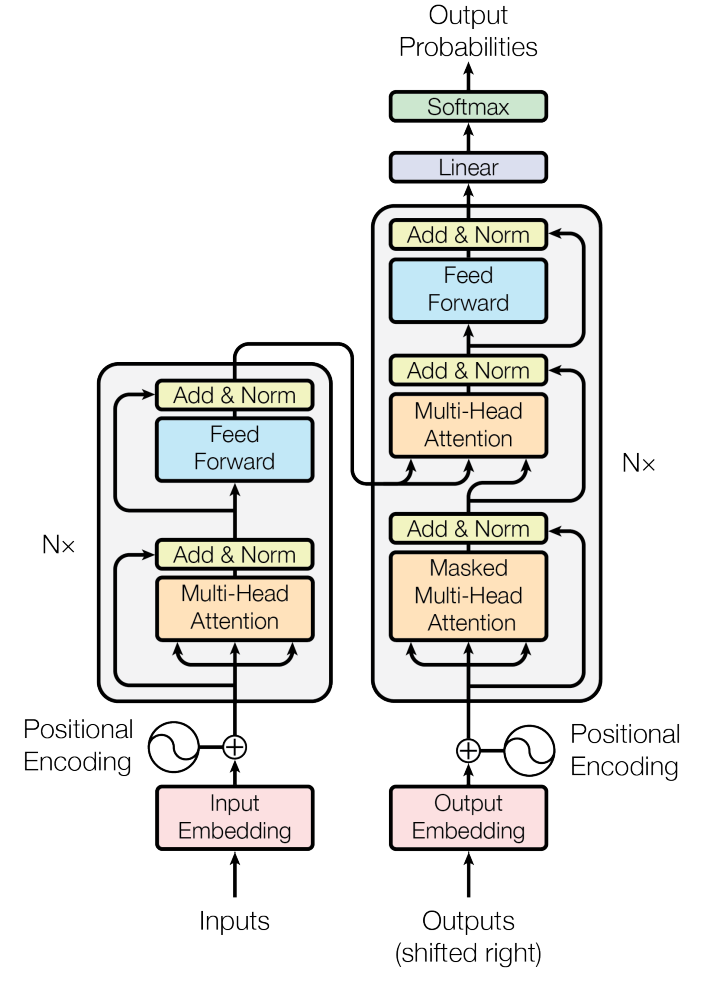
论文下载地址:https://arxiv.org/pdf/1706.03762v7.pdf
代码下载地址:https://github.com/huggingface/transformers
基于Transformer的机器翻译,使用Pytorch深度学习框架实现和gradio实现一个小小的页面
-
编码器(Encoder):
-
对输入序列(如源语言句子)进行编码,生成最终的Key-Value对(Kₑ, Vₑ),并传递给解码器。
-
-
解码器(Decoder):
-
在每一步自回归生成时,解码器会复用编码器的Kₑ, Vₑ(用于交叉注意力),同时还会缓存自身的K₅, V₅(自注意力部分)。
-
"反复加载"的开销:
-
编码器的Kₑ, Vₑ通常较大(与输入序列长度相关),每次生成新token时需从内存加载,导致带宽瓶颈。
-
解码器自身的K₅, V₅也会随生成步骤增长而膨胀(需缓存历史token的KV),进一步加剧内存压力。
-
-
class CausalSelfAttention(nn.Module):
"""
A vanilla multi-head masked self-attention layer with a projection at the end.
It is possible to use torch.nn.MultiheadAttention here but I am including an
explicit implementation here to show that there is nothing too scary here.
"""
def __init__(self, config):
super().__init__()
assert config.n_embd % config.n_head == 0
# key, query, value projections for all heads, but in a batch
self.c_attn = nn.Linear(config.n_embd, 3 * config.n_embd)
# output projection
self.c_proj = nn.Linear(config.n_embd, config.n_embd)
# TODO regularization
self.attn_dropout = nn.Dropout(config.attn_pdrop)
self.resid_dropout = nn.Dropout(config.resid_pdrop)
# TODO 因果掩码,以确保注意力只应用于输入序列中的左侧
self.register_buffer("bias", torch.tril(torch.ones(config.block_size, config.block_size))
.view(1, 1, config.block_size, config.block_size))
self.n_head = config.n_head
self.n_embd = config.n_embd
def forward(self, x):
#TODO 批量大小,序列长度,嵌入维数(n_embd)
B, T, C = x.size() #
# TODO 计算批处理中所有头部的查询、键、值,并将头部向前移动为批处理dim
q, k ,v = self.c_attn(x).split(self.n_embd, dim=2)
k = k.view(B, T, self.n_head, C // self.n_head).transpose(1, 2) # (B, nh, T, hs)
q = q.view(B, T, self.n_head, C // self.n_head).transpose(1, 2) # (B, nh, T, hs)
v = v.view(B, T, self.n_head, C // self.n_head).transpose(1, 2) # (B, nh, T, hs)
# TODO causal self-attention; Self-attend: (B, nh, T, hs) x (B, nh, hs, T) -> (B, nh, T, T)
att = (q @ k.transpose(-2, -1)) * (1.0 / math.sqrt(k.size(-1)))
att = att.masked_fill(self.bias[:,:,:T,:T] == 0, float('-inf'))
att = F.softmax(att, dim=-1)
att = self.attn_dropout(att)
y = att @ v # TODO (B, nh, T, T) x (B, nh, T, hs) -> (B, nh, T, hs)
y = y.transpose(1, 2).contiguous().view(B, T, C) # TODO re-assemble all head outputs side by side
# TODO output projection
y = self.resid_dropout(self.c_proj(y))
return y
论文下载地址:https://arxiv.org/pdf/1911.02150v1.pdf
提出目的和方法
提出目的
多头注意力层作为Transformer神经序列模型中的核心组件,是替代循环神经网络(RNN)实现序列内与序列间信息传递的强大方法。尽管此类层得益于序列长度的并行计算特性使得训练过程通常快速而简单,但在无法实现并行化的增量推理场景中(例如自回归解码,也就是在解码器部分的推理过程中是一步一步的生成最终的结果),其推理速度往往受限于反复加载庞大的"键"与"值"张量所产生的内存带宽开销。
提出方法
提出一种称为"多查询注意力"的变体,通过让所有注意力"头"共享相同的键和值张量,显著压缩了这些张量的规模,从而降低增量解码时的内存带宽需求。实验数据证实,采用该结构的模型在解码速度上获得显著提升,且相较基线模型仅产生轻微的质量损失。
神经注意力
很早之前提出的神经注意力机制是处理变长表征的强大工具。该神经注意力函数接收单个查询向量q和m组不同的(键向量,值向量)配对(以矩阵K和V表示),并生成输出向量y。输出y通过计算各值向量的加权和获得,其中权重来源于查询向量与键向量的相似度比较。
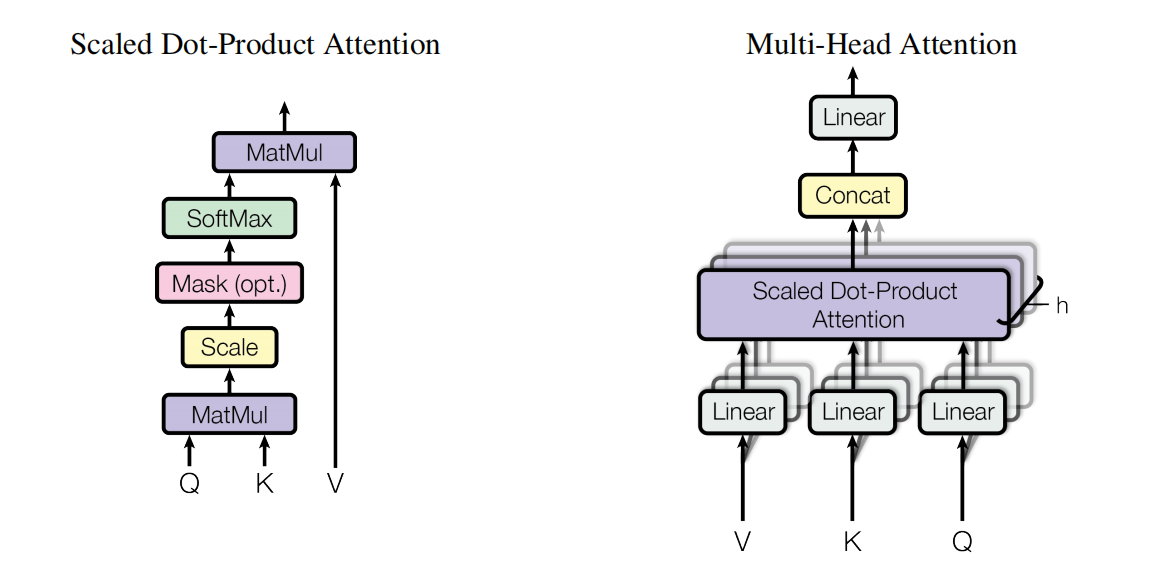
点乘注意力

多头注意力

注解:这里的P_q, P_k, P_v, P_o可以看成是线性变换层,h表示设置的头数。
带有batch维度的多头注意力

注解:这里的mask就可以看成是编码器中对源句子填充部分之后计算自注意力的掩码,以及解码器中计算自注意力时掩盖掉后面的词对当前及之前词的可见性。

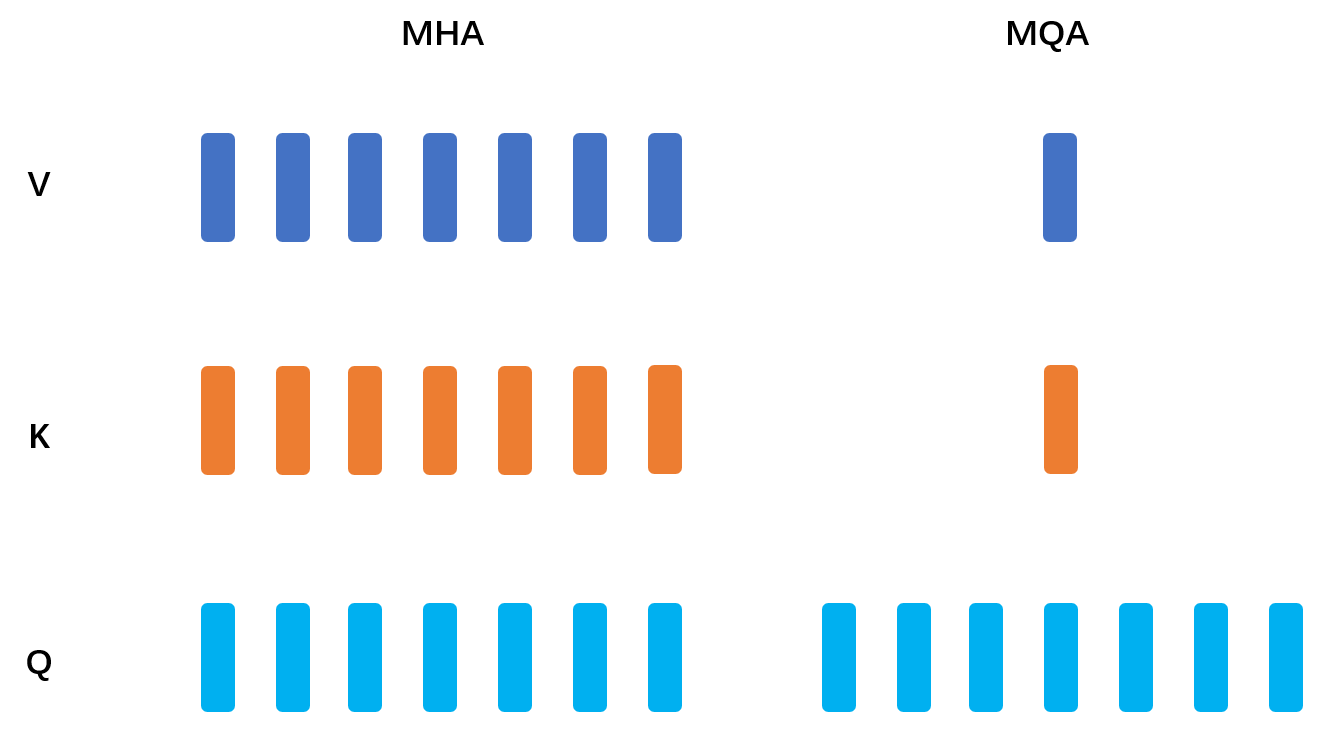
其中嵌入维度为d(词向量长度),由于为多头注意力计算方式,并且设置为h个头,那么每一个投对应d / h大小嵌入维度;因此,对于key和value对应嵌入维度为k = v = d / h;n和m表示输入特征向量对应的维度(序列长度)。
具体计算量的计算方式
先看普通矩阵相乘的计算量
假设有两个矩阵A,B,其中A的维度为[N, M],B的维度为[M, K],那么AB矩阵相乘之后的维度为[N, K],计算量的计算结果:
总计算量:
-
乘法次数:
矩阵 C 有 N×K 个元素,每个元素需要 M 次乘法,因此总乘法次数为:N×M×K -
加法次数:
每个 Cij需要 M−1次加法,因此总加法次数为:N×K×(M−1)
总计算量(浮点运算,FLOPs):
通常,我们将一次乘法和一次加法合并为一次浮点运算(FLOP)。因此,总计算量为:
FLOPs=N×M×K次乘法 + N×K×(M−1)次加法;
近似情况下(当 MM 较大时,忽略 −1−1):
FLOPs≈2×N×M×K
但更常见的是直接以乘法次数 N×M×K 作为计算量的衡量标准。
查询/键/值投影(Q/K/V Projections)
Q = tf.einsum("bnd,hdk->bhnk", X, P_q) # 形状 [b, h, n, k]
K = tf.einsum("bmd,hdk->bhmk", M, P_k) # 形状 [b, h, m, k]
V = tf.einsum("bmd,hdv->bhmv", M, P_v) # 形状 [b, h, m, v]
注意力权重计算(Logits + Softmax)
logits = tf.einsum("bhnk,bhmk->bhnm", Q, K) # 形状 [b, h, n, m]
weights = tf.nn.softmax(logits + mask) # 形状 [b, h, n, m]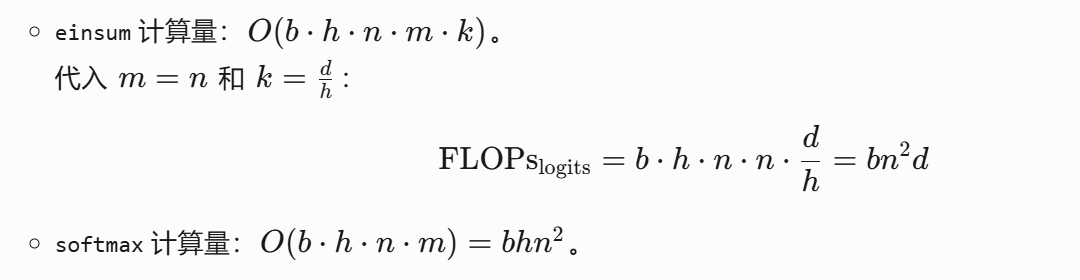
输出投影(Output Projection)
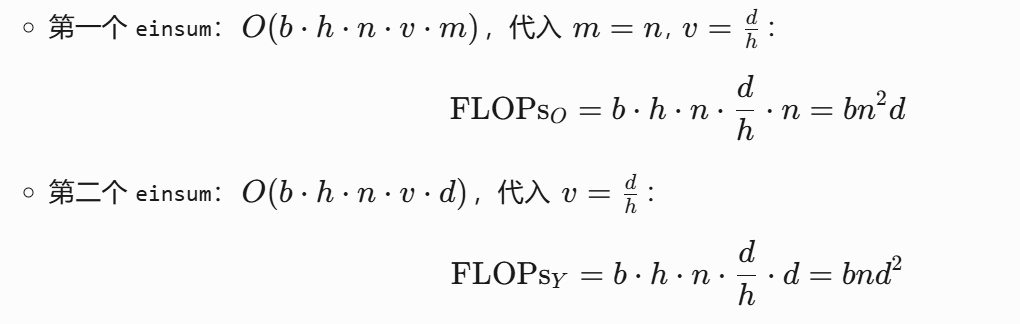
总计算量

内存访问量计算
张量:X, M, Q, K, V, O, Y

张量:logits 和 weights(形状均为 [b,h,n,m],m=n)
2×bhn^2 → O(bhn^2)。
张量:Pq,Pk,Pv,Po(形状 [h,d,k] 或 [h,d,v])
每个投影矩阵大小为 h⋅d⋅hd=d^2,共 4 个 → 4d^2 → O(d^2)。
总的内存访问量
Total MAV=O(bnd)+O(bhn^2)+O(d^2)
内存访问与计算量之比(MAV/FLOPs)

逐步的计算多头注意力

注意:这里的key,value和query来自不同的输入。上面在计算自注意力的时候输入的X维度为[b,n,d],要理解这里的n表示序列长度,也就是输入句子对应tokens的长度,而在解码阶段,通过当前的输入来进行预测下一个词,因此解码过程是一步一步的生成过程,不能通过并行的方式一下子生成多有的词。下面的“逐步的多查询注意力”也是同样的理解。

带有batch的多查询注意力
- 传统多头注意力:每个头有独立的Q、K、V矩阵,内存占用高。

注意:多头查询注意力的key和value在各个头是共享的,因此看到上面对value和key的线性把‘h’给去掉了。
多查询自注意力(逐步的)


import torch
import torch.nn.functional as F
from torch import nn, Tensor, BoolTensor
from typing import Optional
class Attention(nn.Module):
def __init__(self, word_size:int=512, embed_dim:int=64) -> None:
super().__init__()
self.embed_dim = embed_dim
self.dim_K = torch.tensor(embed_dim, requires_grad=False)
self.query = nn.Linear(in_features=word_size, out_features=embed_dim, bias=True)
self.key = nn.Linear(in_features=word_size, out_features=embed_dim, bias=True)
self.value = nn.Linear(in_features=word_size, out_features=embed_dim, bias=True)
def self_attention(self, Q: Tensor, K: Tensor, V: Tensor,
mask:Optional[BoolTensor]=None) -> Tensor:
"""
Perform self-attention on the input tensors.
This is a simple implementation of self-attention that uses the dot product attention mechanism.
If you are looking for attention with better performance, please try:
* `F.scaled_dot_product_attention`
* [Flash Attention](https://github.com/Dao-AILab/flash-attention)
* [Memory-efficient attention](https://facebookresearch.github.io/xformers/components/ops.html)
Args:
Q (torch.Tensor): The query tensor.
K (torch.Tensor): The key tensor.
V (torch.Tensor): The value tensor.
mask (Optional[torch.BoolTensor]): A mask tensor used to hide specific positions in the input sequence.
It should have the same shape as Q, K, and must be a Boolean tensor with 0s indicating positions to be masked.
Use `None` for no masking. Default is `None`.
Returns:
The output tensor of the self-attention layer.
"""
# expected [b, seq, embed_dim]
K_T = torch.transpose(K, -1, -2)
score = torch.matmul(Q, K_T) # Matmul
score /= torch.sqrt(self.dim_K) # Scale
if mask is not None: # Mask (opt.)
score = torch.masked_fill(score, mask==0, -torch.inf)
score = torch.softmax(score, dim=-1) # SoftMax
Z = torch.matmul(score, V) # Matmul
return Z
def forward(self, x:Tensor, mask:Optional[BoolTensor]=None) -> Tensor:
Q = self.query(x)
K = self.key(x)
V = self.value(x)
Z = self.self_attention(Q, K, V, mask=mask)
# Z = F.scaled_dot_product_attention(Q, K, V)
return Z
class MultiheadAttention(nn.Module):
r"""
https://arxiv.org/abs/1706.03762
"""
def __init__(self, word_size: int = 512, embed_dim: int = 64, n_head:int=8) -> None:
super().__init__()
self.n_head = n_head
self.embed_dim = embed_dim
self.dim_K = torch.tensor(embed_dim)
self.proj = nn.Linear(in_features=embed_dim * n_head,
out_features=embed_dim, bias=False)
self.multihead = nn.ModuleList([
Attention(word_size, embed_dim) for _ in range(n_head)
])
def forward(self, x: Tensor, mask:Optional[BoolTensor]=None) -> Tensor:
Z_s = torch.cat([head(x, mask) for head in self.multihead], dim=1)
Z = self.proj(Z_s)
return Z
class MultiQueryAttention(Attention):
r"""
https://arxiv.org/pdf/1911.02150.pdf
"""
def __init__(self, word_size: int = 512, embed_dim: int = 64, n_query:int=8) -> None:
super().__init__(word_size, embed_dim)
self.n_query = n_query
self.proj = nn.Linear(in_features=embed_dim * n_query,
out_features=embed_dim, bias=False)
delattr(self, 'query')
self.querys = nn.ModuleList([
nn.Linear(in_features=word_size, out_features=embed_dim, bias=True)
for _ in range(n_query)
])
self.key = nn.Linear(in_features=word_size, out_features=embed_dim, bias=True)
self.value = nn.Linear(in_features=word_size, out_features=embed_dim, bias=True)
def forward(self, x: Tensor, mask:Optional[BoolTensor]=None) -> Tensor:
K = self.key(x)
V = self.value(x)
Z_s = torch.cat([
self.self_attention(query(x), K, V, mask) for query in self.querys
], dim=1)
Z = self.proj(Z_s)
return Z综合实验
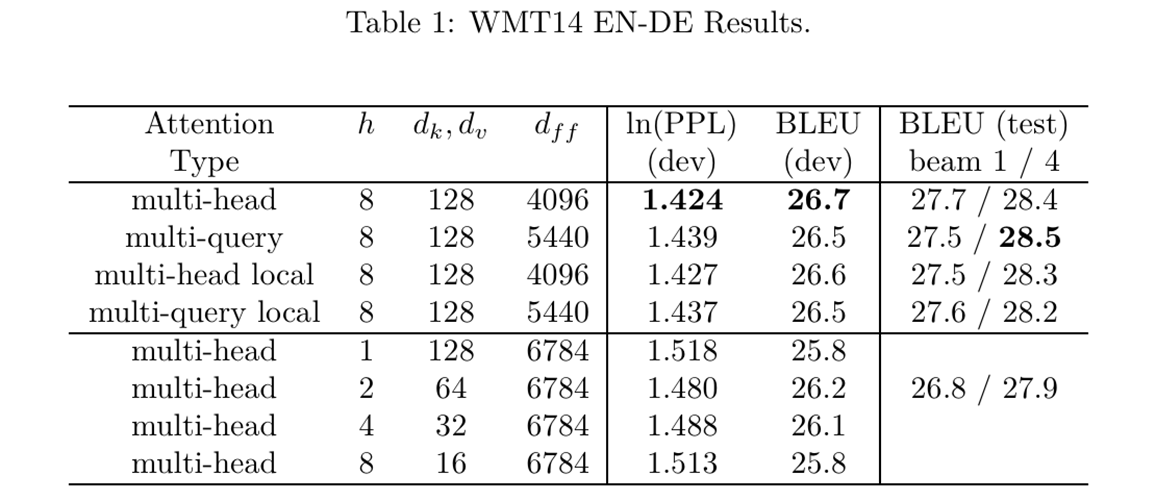
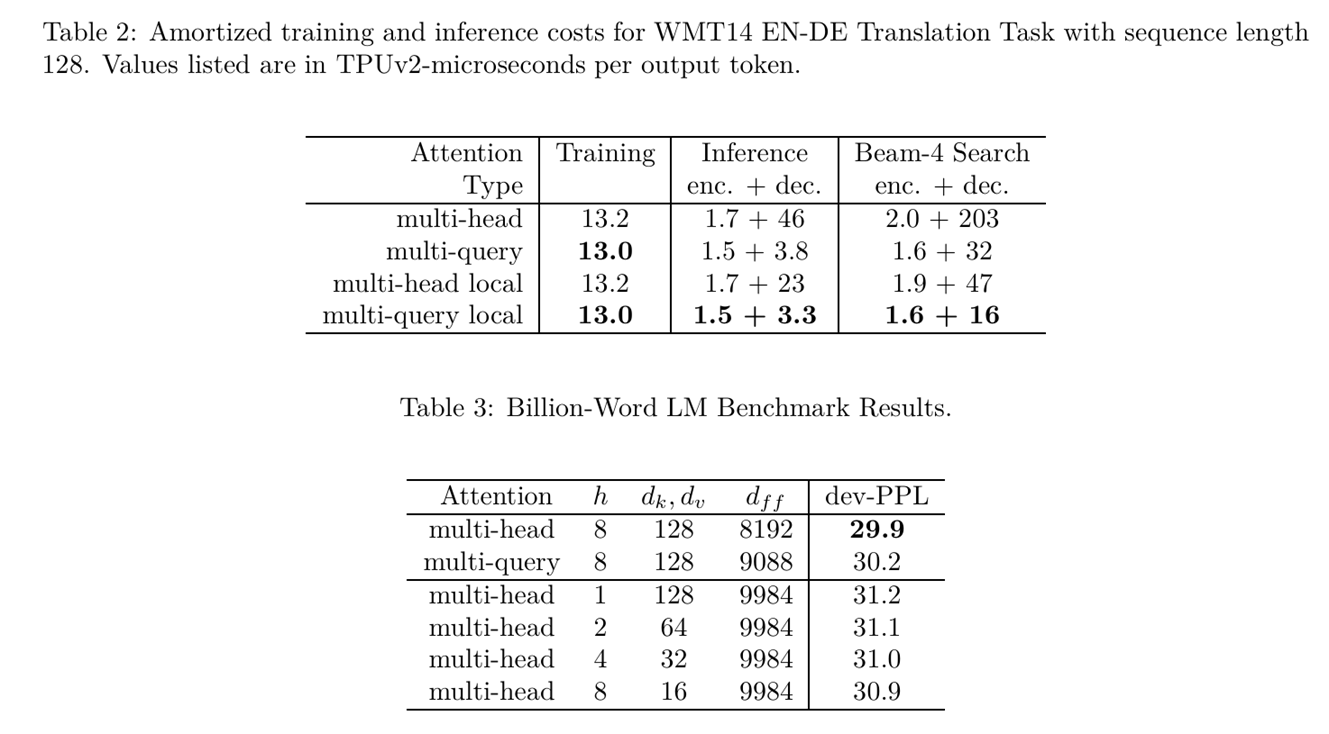

























 1728
1728

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








