代码随想录算法训练营第三十八天|动态规划理论基础 509. 斐波那契数 70. 爬楼梯 746. 使用最小花费爬楼梯-优快云博客

文章详细介绍了动态规划的概念，强调了其解决具有重叠子问题的特点。解题步骤包括确定DP数组、递推公式、初始化、遍历顺序，并通过斐波那契数列和爬楼梯问题作为示例进行讲解。调试动态规划问题的关键是打印并检查DP数组。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

理论基础

1、什么是动态规划？
动态规划，英文：Dynamic Programming，简称DP，如果某一问题有很多重叠子问题，使用动态规划是最有效的。
动态规划中每一个状态一定是由上一个状态推导出来的，这一点就区分于贪心，贪心没有状态推导，而是从局部直接选最优的

2、动态规划的解题步骤
对于动态规划问题，我将拆解为如下五步曲，这五步都搞清楚了，才能说把动态规划真的掌握了！

确定dp数组（dp table）以及下标的含义
确定递推公式
dp数组如何初始化
确定遍历顺序
举例推导dp数组

一些情况是递推公式决定了dp数组要如何初始化！

3、动态规划应该如何debug？
找问题的最好方式就是把dp数组打印出来，看看究竟是不是按照自己思路推导的！
做动规的题目，写代码之前一定要把状态转移在dp数组的上具体情况模拟一遍，心中有数，确定最后推出的是想要的结果。

然后再写代码，如果代码没通过就打印dp数组，看看是不是和自己预先推导的哪里不一样。
如果打印出来和自己预先模拟推导是一样的，那么就是自己的递归公式、初始化或者遍历顺序有问题了。
如果和自己预先模拟推导的不一样，那么就是代码实现细节有问题。

这道题目我举例推导状态转移公式了么？
我打印dp数组的日志了么？
打印出来了dp数组和我想的一样么？
如果这灵魂三问自己都做到了，基本上这道题目也就解决了，或者更清晰的知道自己究竟是哪一点不明白，是状态转移不明白，还是实现代码不知道该怎么写，还是不理解遍历dp数组的顺序。

509. 斐波那契数

题目链接

详细的分析写在了注释里面，对自己学习还需要去代码随想录网站上仔细看。
还可以优化只维护3个变量完成实现，空间复杂度更小。

class Solution {
public:
    int fib(int n) {
        // 动态规划五部曲
        // 1、确定dp[i]的含义：第i个斐波那契数的值
        // 2、确定递归公式  dp[i] = dp[i-1] + dp[i-2]
        // 3、dp数组初始化：dp[0] = 0 dp[1] = 1
        // 4、遍历顺序： 从前往后
        // 5、打印dp数组验证
        if (n == 0 || n == 1) return n;
        vector<int> dp(n+1);
        dp[0] = 0;
        dp[1] = 1;
        for (int i = 2; i <= n; i++) {
            dp[i] = dp[i-1] + dp[i-2];
        }
        return dp[n];
    }
};

70. 爬楼梯

题目链接

确定dp数组以及下标的含义
dp[i]：爬到第i层楼梯，有dp[i]种方法
确定递推公式
如何可以推出dp[i]呢？
从dp[i]的定义可以看出，dp[i] 可以有两个方向推出来。
首先是dp[i - 1]，上i-1层楼梯，有dp[i - 1]种方法，那么再一步跳一个台阶不就是dp[i]了么。
还有就是dp[i - 2]，上i-2层楼梯，有dp[i - 2]种方法，那么再一步跳两个台阶不就是dp[i]了么。
那么dp[i]就是 dp[i - 1]与dp[i - 2]之和！
所以dp[i] = dp[i - 1] + dp[i - 2] 。
在推导dp[i]的时候，一定要时刻想着dp[i]的定义，否则容易跑偏。
这体现出确定dp数组以及下标的含义的重要性！
dp数组如何初始化 dp[1] = 1，dp[2] = 2
题目中说了n是一个正整数，题目根本就没说n有为0的情况。
所以本题其实就不应该讨论dp[0]的初始化！
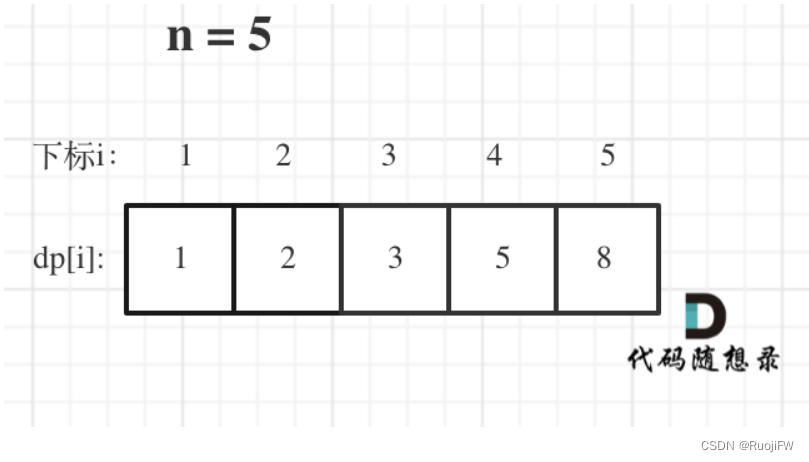
举例推导dp数组
举例当n为5的时候，dp table（dp数组）应该是这样的

class Solution {
public:
    int climbStairs(int n) {
        // 1、确定dp数组的含义：爬楼梯的方法
        // 2、确定地推公式： dp[i] = dp[i-1] + dp[i-2]
        // 3、dp数组初始化：dp[1] = 1  dp[2] = 2
        // 4、遍历顺序：从小到大
        if (n == 1) return n;
        int dp[3];
        dp[1] = 1;
        dp[2] = 2;
        for (int i = 3; i <=n; i++) {
            int sum = dp[1] + dp[2];
            dp[1] = dp[2];
            dp[2] = sum;
        }
        return dp[2];
    }
};

746. 使用最小花费爬楼梯

题目链接

class Solution {
public:
    int minCostClimbingStairs(vector<int>& cost) {
        int dp0 = 0;
        int dp1 = 0;
        for (int i = 2; i <= cost.size(); i++) {
            int dpi = min(dp1 + cost[i - 1], dp0 + cost[i - 2]);
            dp0 = dp1; // 记录一下前两位
            dp1 = dpi;
        }
        return dp1;
    }
};