Leetcode（304）——二维区域和检索 - 矩阵不可变

Leetcode（304）——二维区域和检索 - 矩阵不可变

题目

给定一个二维矩阵 matrix，以下类型的多个请求：

• 计算其子矩形范围内元素的总和，该子矩阵的 左上角 为 (row1, col1) ，右下角 为 (row2, col2) 。

实现 NumMatrix 类：

• NumMatrix(int[][] matrix) 给定整数矩阵 matrix 进行初始化
• int sumRegion(int row1, int col1, int row2, int col2) 返回 左上角 (row1, col1) 、右下角 (row2, col2) 所描述的子矩阵的元素 总和 。

示例 1：

输入：
[“NumMatrix”,“sumRegion”,“sumRegion”,“sumRegion”]
[[[[3,0,1,4,2],[5,6,3,2,1],[1,2,0,1,5],[4,1,0,1,7],[1,0,3,0,5]]],[2,1,4,3],[1,1,2,2],[1,2,2,4]]
输出：
[null, 8, 11, 12]
解释：
NumMatrix numMatrix = new NumMatrix([[3,0,1,4,2],[5,6,3,2,1],[1,2,0,1,5],[4,1,0,1,7],[1,0,3,0,5]]);
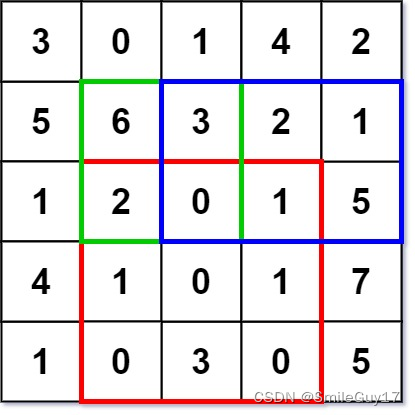
numMatrix.sumRegion(2, 1, 4, 3); // return 8 (红色矩形框的元素总和)
numMatrix.sumRegion(1, 1, 2, 2); // return 11 (绿色矩形框的元素总和)
numMatrix.sumRegion(1, 2, 2, 4); // return 12 (蓝色矩形框的元素总和)

提示：

• m == matrix.length
• n == matrix[i].length
• 1 <= m, n <= 200
• $-10^5$ <= matrix[i][j] <= $10^5$
• 0 <= row1 <= row2 < m
• 0 <= col1 <= col2 < n
• 最多调用 $10^4$ 次 sumRegion 方法

题解

关键：做这种初始化一次、检索多次的题目的秘诀：在初始化的时候做好预处理

方法一：暴力枚举

思路

​​  依旧是熟悉的暴力枚举，我们将 左上角 (row1, col1) 和右下角 (row2, col2) 所构成的矩形中的元素一一进行遍历，然后相加获得最后的值。

代码实现

class NumMatrix {
    vector<vector<int>>& value;
public:
    NumMatrix(vector<vector<int>>& matrix) : value(matrix){}
    
    int sumRegion(int row1, int col1, int row2, int col2) {
        int ans = 0;
        for(int n = row1; n <= row2; n++){     // 行
            for(int m = col1; m <= col2; m++){ // 列
                ans += value[n][m];
            }
        }
        return ans;
    }
};

复杂度分析

时间复杂度：每次查找的时间复杂度都为 $O(N\ast M)$ ，其中 $N$ 是左上角与右下角的横坐标之差的绝对值， $M$ 是左上角与右下角的纵坐标之差的绝对值。
空间复杂度：$O(T)$，$T$ 表示输入数组的元素个数。

方法二：二维数组的前缀和

思路

​​  和 Leetcode-303 一样，我们先进行预处理，即求出前缀和，只是这次的前缀和，即 PreSum [i][j] 是指以 (0,0) 为左上角，以 (i,j) 为右下角的矩形中值的和。
​​  那么如何通过前缀和来获得左上角 (row1, col1) 和 右下角 (row2, col2) 所构成的矩形中元素之和呢？
​​  仔细观察可以发现这个公式：
$$preSum[row2][col2]-preSum[row2][col1-1]-preSum[row1-1][col2]+preSum[row1-1][col1-1]$$

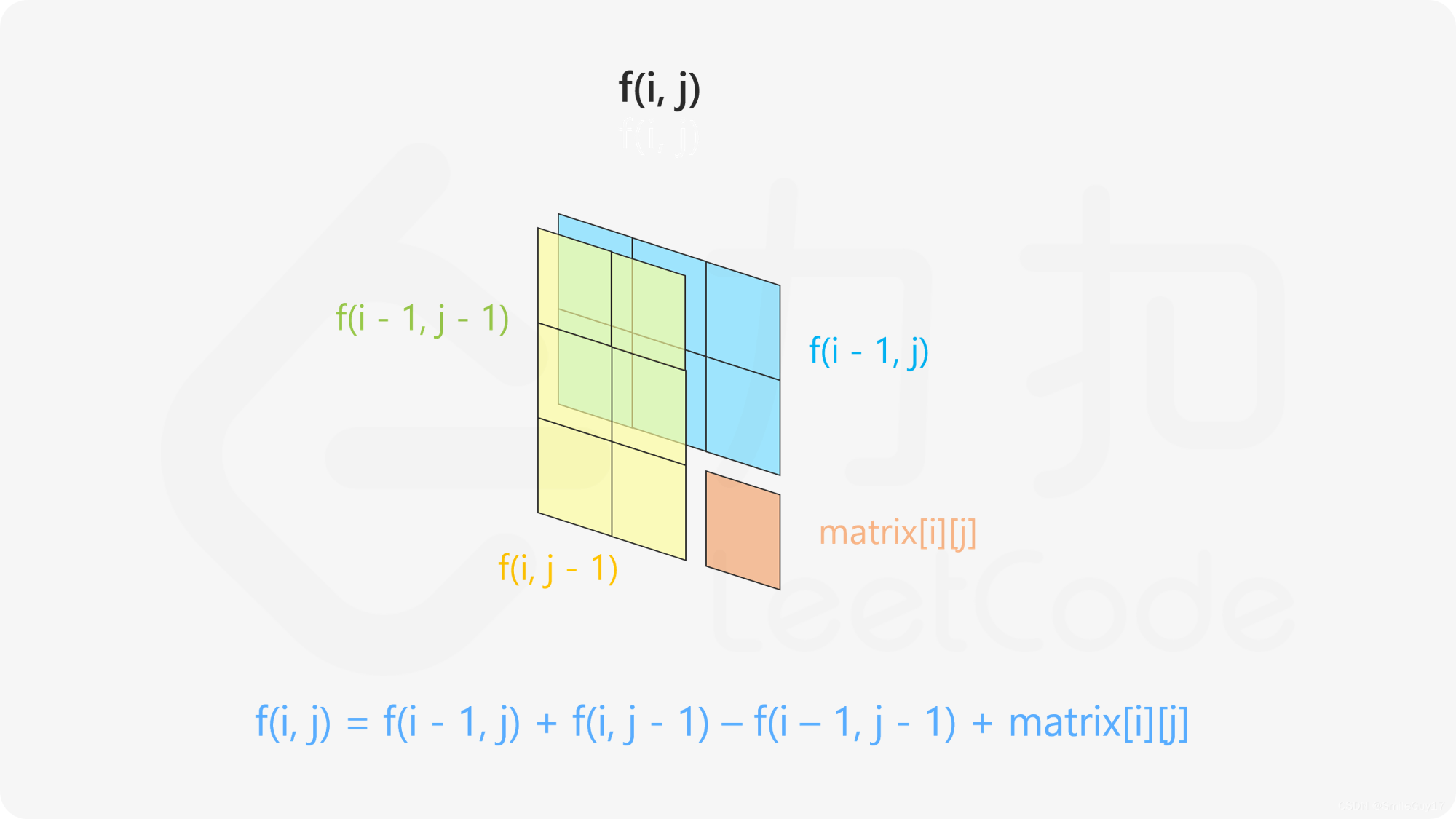
​​  但是为了让第 0 行与第 0 列的元素也能使用上面的递推公式。如果 PreSum 矩阵大小和 martix 大小相等，则需要对第 0 行与第 0 列特殊判断。

算法实现：

1. 在初始化时求出前缀和；
2. 在调用 sumRegion 时使用公式返回对应值。

代码实现

优化前：（自己最初写的）

class NumMatrix {
    vector<vector<int>> Presum;
public:
    NumMatrix(vector<vector<int>>& matrix) {
        int i = matrix[0].size(), j = matrix.size();
        Presum.resize(j);
        for(int n = 0; n < j; n++){     // 行
            Presum[n].resize(i);
            if(n == 0){
                Presum[n][0] = matrix[n][0];
            }else Presum[n][0] = matrix[n][0] + Presum[n-1][0];
            for(int m = 1; m < i; m++){ // 列
                if(n == 0){
                    Presum[n][m] = Presum[n][m-1] + matrix[n][m];
                }else Presum[n][m] = matrix[n][m] + Presum[n][m-1] + Presum[n-1][m] - Presum[n-1][m-1];
            }
        }
    }
    
    int sumRegion(int row1, int col1, int row2, int col2) {
        if(row1 != 0 && col1 != 0){
            return Presum[row2][col2] - Presum[row1-1][col2] - Presum[row2][col1-1] + Presum[row1-1][col1-1];
        }else if(row1 == 0 && col1 != 0){
            return Presum[row2][col2] - Presum[row2][col1-1];
        }else if(col1 == 0 && row1 != 0){
            return Presum[row2][col2] - Presum[row1-1][col2];
        }else return Presum[row2][col2]; // row1 和 col1 都为 0
    }
};

优化后：

class NumMatrix {
public:
    vector<vector<int>> Presum;

    NumMatrix(vector<vector<int>>& matrix) {
        int m = matrix.size();
        if (m > 0) {
            int n = matrix[0].size();
            Presum.resize(m + 1, vector<int>(n + 1));
            for (int i = 0; i < m; i++) {
                for (int j = 0; j < n; j++) {
                    Presum[i + 1][j + 1] = Presum[i][j + 1] + Presum[i + 1][j] - Presum[i][j] + matrix[i][j];
                }
            }
        }
    }

    int sumRegion(int row1, int col1, int row2, int col2) {
        return Presum[row2 + 1][col2 + 1] - Presum[row1][col2 + 1] - Presum[row2 + 1][col1] + Presum[row1][col1];
    }
};

复杂度分析

时间复杂度：初始化 $O(m\ast n)$，每次检索 $O(1)$，其中 $m$ 和 $n$ 分别是矩阵 $\text{matrix}$ 的行数和列数。初始化需要遍历矩阵 $\text{matrix}$ 计算二维前缀和，时间复杂度是 $O(mn)$。每次检索的时间复杂度是 $O(1)$。
空间复杂度：$O(T)$，$T$ 表示输入数组的元素个数。