霍夫变换原理及实现

目录

 

一霍夫变换原理

二 霍夫变换实现方法

三 参考文献

---

一霍夫变换原理

根据数学对偶性原理提出了检测图像直线的方法,主要应用于模式识别领域中对二值图像进行直线检测。在图像空间XY里，所有过点(x,y)的直线都满足方程:

y = px + q (1)

其中p为斜率，q为截距。式(1)也可以写成

q = -px+ y (2)

式(2)可以认为代表参数空间PQ中过点(p,q)的1条直线。

由此可知在图像空间中共线的点对应在参数空间里相交的线。亦即在参数空间中相交于同一点的所有直线在图像空间里都有共线的点与之对应。霍夫变换根据这些关系把在图像空间中的检测问题转换到参数空间里，通过在参数空间里进行简单的累加统计完成检测任务。式(1)在直线接近竖直方向时将使p和q都接近于无穷而大大增加计算量，因此我们可以用直线的极坐标方程

r= x cos t+ y sin t (3)

这样原图像空间XY中的点对应于新参数空间中的一条正弦曲线。检测在图像空间共点的直线需要在参数空间里检测正弦曲线的交点。其方法是对图像空间中的每一点(x,y) ,依据式(3)对参数空间中所有可能的值算出相应的r值，并对该(r, t)对进行累加。这样累加值大于我们预定阈值的(r, t)对应于图像空间中所要检测的直线。

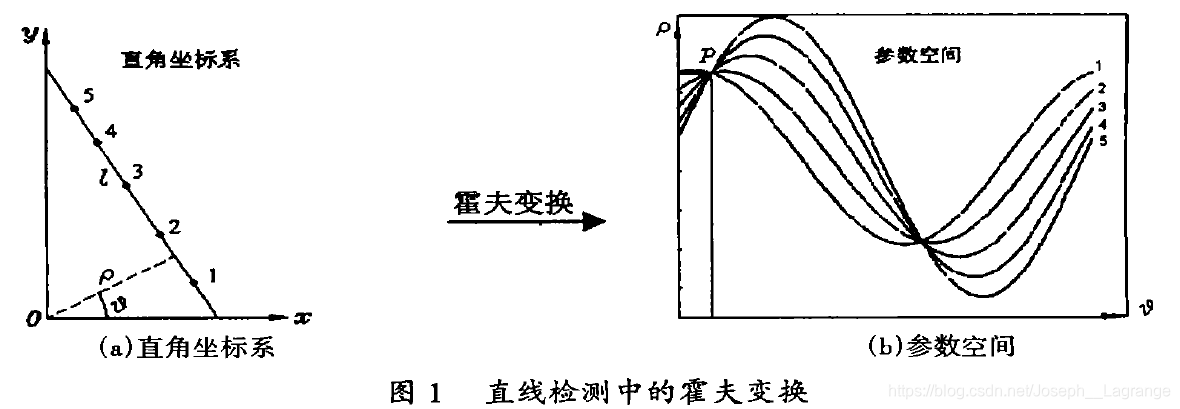
由上述霍夫变换原理可知, 霍夫变换具有如下性质：

(1)直角坐标系中的一个点映射到参数空间中为一条曲线;

(2)参数空间中的一个点对应直角坐标系中的一条直线;

(3)直角坐标系中的共点线映射到参数空间中为一条曲线;

(4)直角坐标系中的共线点映射到参数空间中后为一个交于同一点的曲线族。

二 霍夫变换实现方法

工程中的实验数据和图像处理中的二值边缘图, 通常都是离散数据, 因此, 根据霍夫变换性质, 可按下列步骤实现霍夫变换:

(1)将参数空间量化为m×n(m为t的等份数, n为r的等份数)个单元,并设置累加器矩阵Qm×n；

(2)给参数空间中的每个单元分配一个累加器Q(i,j), 并把累加器的初始值置为零;

(3)取出直角坐标系中的点(xi,yi)(i=1,2,3 …s, s为直角坐标系中的已知点数)代入式(3) 并以量化后的t值计算出r;

(4)在参数空间中, 找到t和r所对应的单元,并将该单元的累加器加1,即Q(i,j)=Q(i,j)+1 ;

(5)当直角坐标系中的点都经过(3)、(4)两步遍历后, 检验参数空间中每个累加器的值, 累加器值最大的单元所对应的t和r即为直角坐标系中直线方程式(3)的参数。

由上述霍夫变换过程可知, 如果参数空间中t和r的量化过粗,则参数空间中的凝聚效果较差, 找不出直线的准确参数t和r;反之, t和r量化过细, 那么计算量将增大。

三 参考文献

邱桑敏, & 夏雨人. (2004). 一种快速霍夫变换算法. 计算机工程, 30(2), 148-150.

曾接贤, 张桂梅, 储珺, & 鲁宇明. (2003). 霍夫变换与最小二乘法相结合的直线拟合. 南昌航空大学学报: 自然科学版, (4), 9-13.

唐佳林, 王镇波, and 张鑫鑫. "基于霍夫变换的直线检测技术." 科技信息 14 (2011): I0033-I0033.