排序算法之堆排序及Python实现

面试中经常会被问到排序算法，其中快速排序、归并排序、堆排序最有可能会被问到，它们的相似的地方在于算法复杂度均为O(nlogn)，其中快排和归并排序前面已经介绍过，今天我们来学习一下堆排序。

堆排序基本概念

堆排序是利用堆进行排序的，堆是一种完全二叉树。完全二叉树是一种除了最后一层之外的其他每一层都被完全填充，并且所有结点都保持向左对齐的树。

堆有两种类型: 大根堆小根堆

两种类型的概念如下：
大根堆：每个结点的值都大于或等于左右孩子结点
小根堆：每个结点的值都小于或等于左右孩子结点

堆的基本思想

1、首先将待排序的数组构造出一个大根堆；
2、取出这个大根堆的堆顶节点(最大值)，与堆的最下最右的元素进行交换，然后把剩下的元素再构造出一个大根堆；
3、重复第二步，直到这个大根堆的长度为1，此时完成排序。

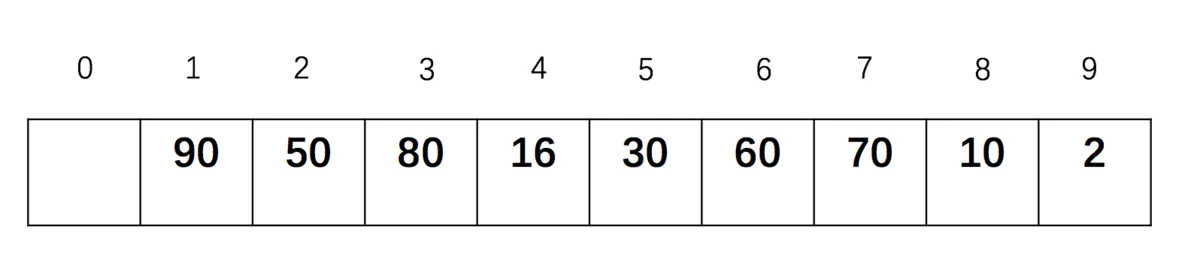
写代码的时候，会遇到这样的问题：
1、如何把一个序列构造出一个大根堆
2、输出堆顶元素后，如何使剩下的元素构造出一个大根堆

在阵列起始位置为0的情况中：

1、父节点i的左子节点在位置(2i+1);
2、父节点i的右子节点在位置(2i+2);
3、子节点i的父节点在位置(i-1)//2;

第一个问题：构造大根堆

'''
其实就两个过程，一个是建立最大堆，另一个是维护最大堆
最大堆定义：父节点大于子节点

'''
def heap_sort(ary) :
    n = len(ary)
    first = int(n/2-1)       #最后一个非叶子节点，也就是第n个子节点的父节点
    for start in range(first,-1,-1) :     #循环每个父节点构造大根堆
        print("构建大根堆：",max_heapify(ary,start,n-1))
    for end in range(n-1,0,-1):           #堆排，将大根堆转换成有序数组
        ary[end],ary[0] = ary[0],ary[end]
        print("转换有序数组",max_heapify(ary,0,end-1))
    return ary


#最大堆调整：将堆的末端子节点作调整，使得子节点永远小于父节点
#start为当前需要调整最大堆的位置，end为调整边界
def max_heapify(ary,start,end):
    root = start
    while True :
        child = root*2 +1               #调整节点的子节点
        if child > end : break       #判断是否存在子节点，如果child>end则表示不存在子节点
        if child+1 <= end and ary[child] < ary[child+1] :  #存在右子节点，并且左子节点小于右子节点
            child = child+1             #取较大的子节点
        if ary[root] < ary[child] :     #较大的子节点成为父节点
            ary[root],ary[child] = ary[child],ary[root]     #交换
            root = child
        else :
            # print("one")
            break
    return ary


print("max_heap:",max_heapify([6,4,10,2,5,3],0,5))
print((heap_sort([6,4,10,1,5,3])))

堆排序的复杂度

建堆是一个线性过程，从len/2-0一直调用堆调整的过程，相当于o(h1)+o(h2)+…+o(hlen/2)这里的h表示节点深度，len/2表示节点最大深度，对于求和过程，结果为线性的O(n) 。

堆调整为一个递归的过程，调整堆的过程时间复杂度与堆的深度有关系，相当于lgn的操作。

建堆的时间复杂度是O(n)，调整堆的时间复杂度是O(lgn)，所以堆排序的时间复杂度是O(nlgn)。