数据结构第六章查找(二) 散列表(Hash)，KMP

最新推荐文章于 2025-08-26 10:28:27 发布

原创最新推荐文章于 2025-08-26 10:28:27 发布 · 194 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#数据结构 #哈希表 #KMP

数据结构专栏收录该内容

27 篇文章

订阅专栏

本文深入探讨了哈希表中的负载因子概念，介绍了多种哈希函数的实现，如除余法、乘余取整法等，并详细阐述了开散列（拉链法）和闭散列（开放寻址法）解决冲突的策略，包括线性探查、二次探查和随机探查。同时，提到了KMP算法在字符串匹配中的应用，讨论了其如何利用最长公共前后缀避免不必要的比较。最后，总结了散列表中解决冲突的两种主要方法：开放地址法和链地址法。

1.负载因子

负载因子= $已有元素数组长度\frac{已有元素}{数组长度}$

2.哈希函数

[1] 除余法h(x) = x % M
[2] 乘余取整法 h(x) = floor(n * (A * x的小数部分))
[3] 平方取中法先平方，然后取中间几位
[4] 基数转换法换成其他进制，然后取其中几位
[5] ELFhash字符串

2种哈希算法

1.开散列方法（拉链法）
2.闭散列方法（开放寻址法）
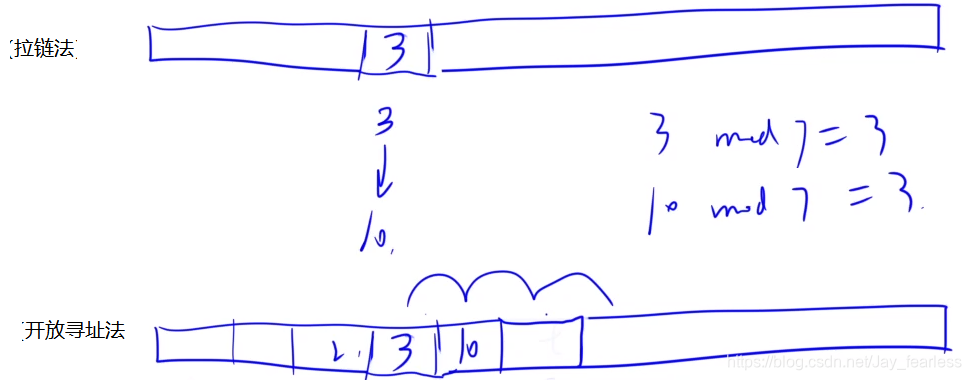
在这里插入图片描述

聚集和二级聚集

a. 线性探查法 d(i) = (d(0) + i * c) % M。易产生聚集问题。
b. 二次探查法。易产生二级聚集问题。
d(2i - 1) = (d(0) + i^2) % M
d(2i) = (d(0) - d ^2) % M
c. 随机探查法。易产生二级聚集问题。
d. 双散列探查法

拉链法

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 2e5+3;
int n,x,idx;
char op[2];
int h[N],e[N],ne[N];
void add(int a, int b)
{
    e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}
bool check(int t,int x)
{
    for(int i=h[t];~i;i=ne[i])
    {
        if(e[i]==x) return true;
    }
    return false;
}
int main()
{
    memset(h,-1,sizeof h);
    scanf("%d", &n);
    for(int i=0;i<n;i++)
    {
        scanf("%s",op);
        if(*op=='I'){
            scanf("%d",&x);
            int t=(x%N+N)%N;
            if(!check(t,x))
                add(t,x);
        }
        else{
            scanf("%d",&x);
            int t=(x%N+N)%N;
            if(check(t,x)) puts("Yes");
            else puts("No");
        }
    }
    
    return 0;
}

开放寻址法

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 2e5+3,INF=0x3f3f3f3f;
int n,x,idx;
char op[2];
int h[N];
int find(int x)
{
    int t=(x%N+N)%N;
    while(h[t]!=INF && h[t]!=x)
        t=(t+1)%N;
    return t;
}
int main()
{
    memset(h,0x3f,sizeof h);
    scanf("%d", &n);
    for(int i=0;i<n;i++)
    {
        scanf("%s%d",op,&x);
        if(*op=='I')
        {
            h[find(x)]=x;
        }
        else{
            if(h[find(x)]==INF) puts("No");
            else puts("Yes");
        }
    }
    return 0;
}

3.KMP算法

ne[i]：前i个字母构成的字符串中，最长的前缀相等的后缀长度
在这里插入图片描述

KMP算法代码

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 100010, M = 1000010;

int n, m;
char p[N], s[M];
int ne[N];

int main()
{
    scanf("%d%s", &n, p + 1);
    scanf("%d%s", &m, s + 1);
	
	//求ne数组
    for (int i = 2, j = 0; i <= n; i ++ )
    {
        while (j && p[i] != p[j + 1]) j = ne[j];
        if (p[i] == p[j + 1]) j ++ ;
        ne[i] = j;
    }

	//求匹配情况
    for (int i = 1, j = 0; i <= m; i ++ )
    {
        while (j && s[i] != p[j + 1]) j = ne[j];
        if (s[i] == p[j + 1]) j ++ ;
        if (j == n) printf("%d ", i - n);
    }
    return 0;
}

散列表中解决冲突的两种方法是（开放地址法）和（链地址法）。