1.最小生成树

1.Prim算法
1.朴素算法 O(n2)O(n^2)O(n2),适合稠密图
2.堆优化写法 O(mlogn)O(mlogn)O(mlogn),适合稀疏图
当m=n2m=n^2m=n2时,堆优化写法比朴素写法慢,所以适合稀疏图。
2.Kruskal算法(并查集)
2.最短路
1.单源最短路 Dijkstra算法,贪心思想O(n2)O(n^2)O(n2)
2.多源汇最短路 Floyd,动态规划思想O(n3)O(n^3)O(n3)
3.关键路径
1.AOE网
2.关键路径:由于AOE网中的有些活动是可以并行进行的(如活动 a1a_1a1、a2a_2a2 和 a3a_3a3 就是可以并行进行的),所以完成工程的最短时间是从源点到汇点的最长路径的长度。路径长度最长的路径就叫做 关键路径(Critical Path)。
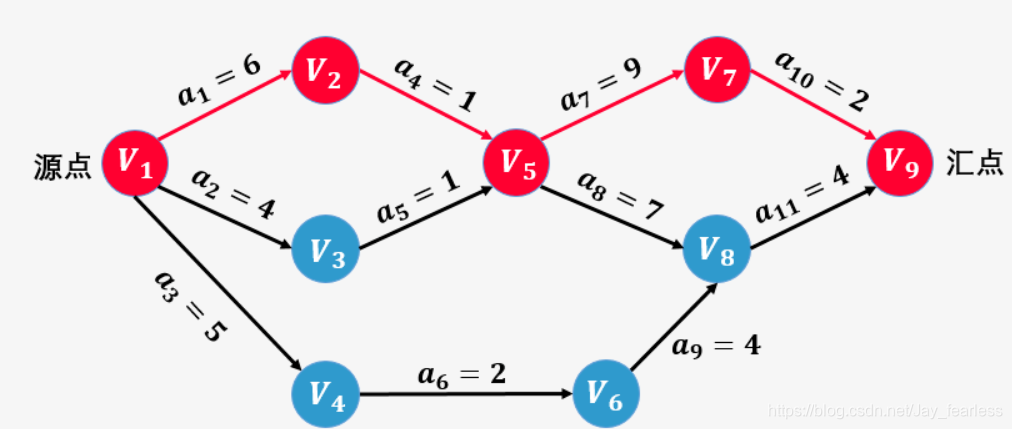
关键路径是活动的集合,而不是事件的集合。
关键路径的查找过程中主要涉及四个概念,事件(顶点)的最早发生时间ETV,事件(顶点)的最晚发生时间LTV,活动(弧)的最早发生时间ETE,活动(弧)的最晚发生时间为LTE。
1.ETV(Earliest Time Of Vertex):事件最早发生时间,就是顶点的最早发生时间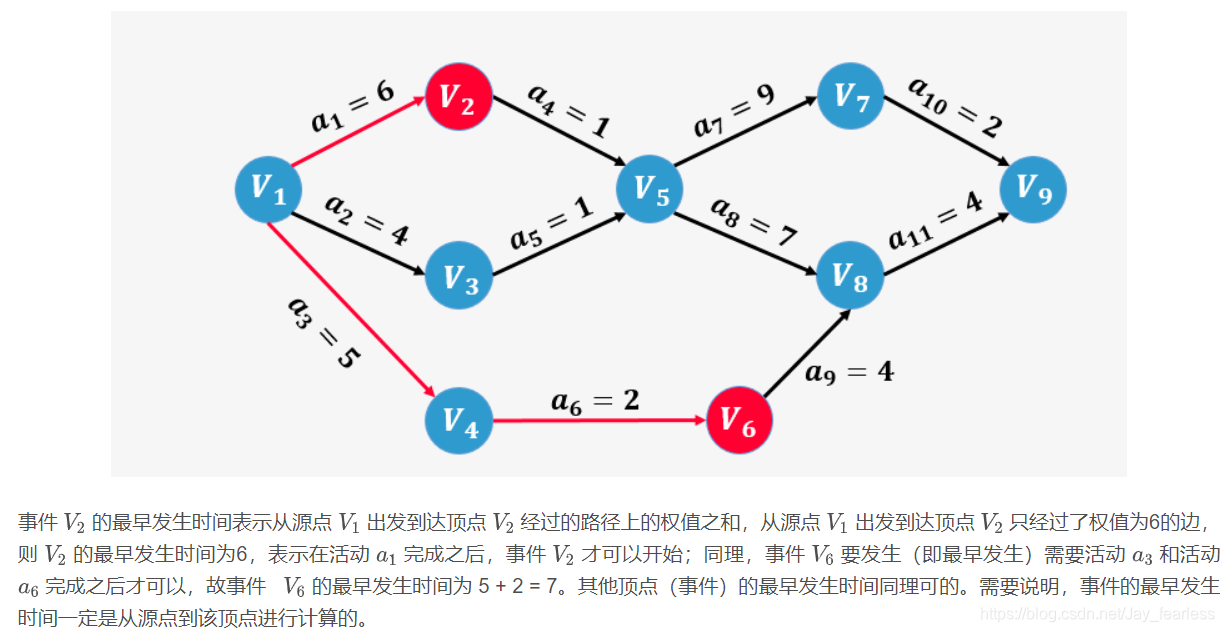
2.LTV(Latest Time Of Vertex):事件最晚发生时间,就是每个顶点对应的事件最晚需要开始的时间,如果超出此时间将会延误整个工期。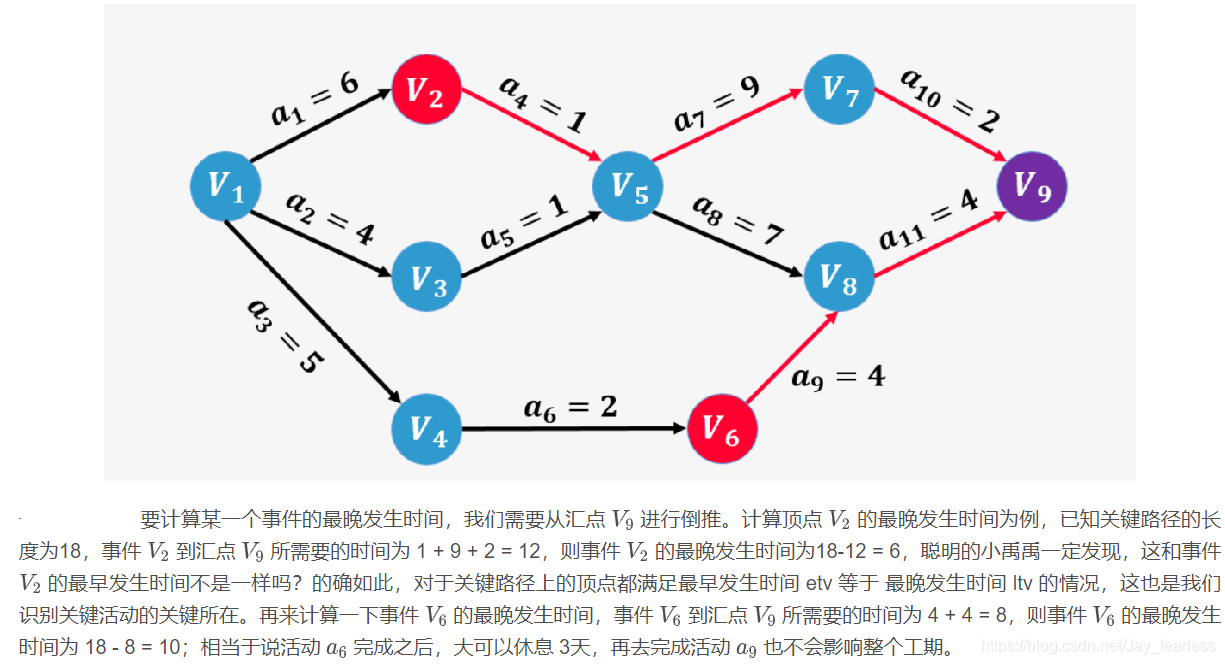
3.ETE(Earliest Time Of Edge):活动的最早开工时间,就是弧的最早发生时间。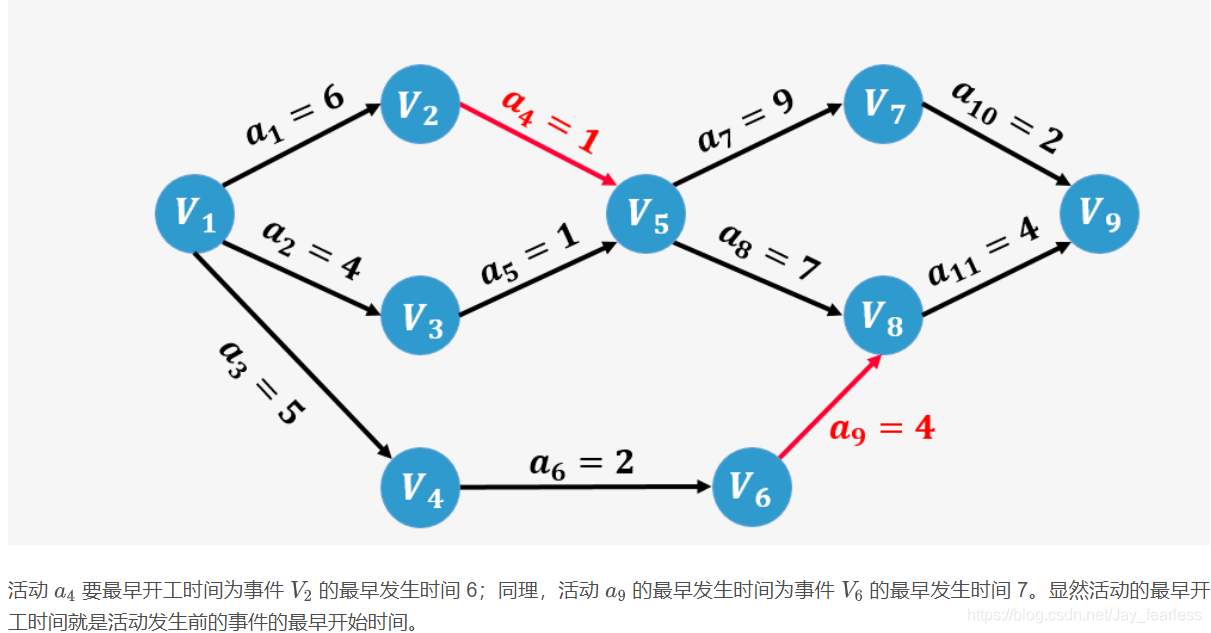
4.LTE(Lastest Time of Edge):活动的最晚发生时间,就是不推迟工期的最晚开工时间。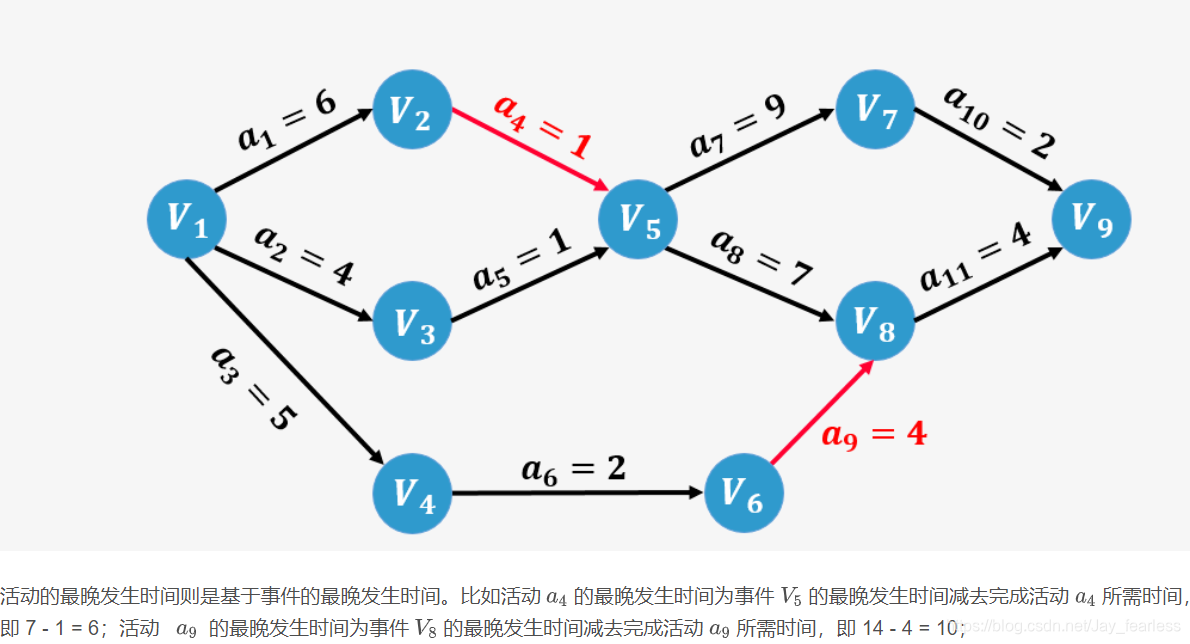 #### DFS,BFS对比:
#### DFS,BFS对比:
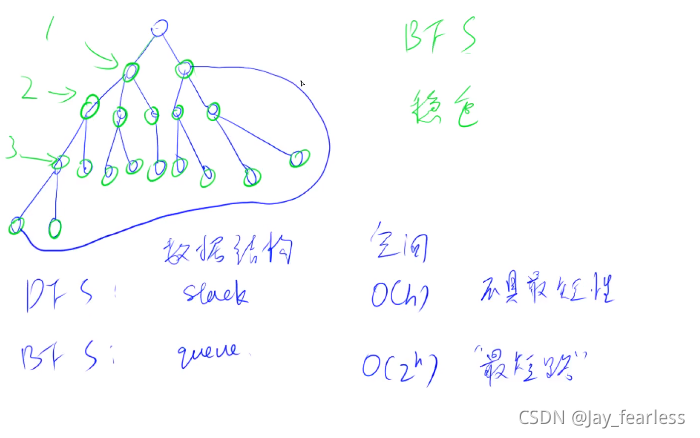





 本文深入探讨了图论中两种核心算法——最小生成树算法(包括Prim算法和Kruskal算法)及最短路径算法(包括Dijkstra算法和Floyd算法)。此外还介绍了关键路径的概念及其在AOE网络中的应用,并简要比较了DFS与BFS算法。
本文深入探讨了图论中两种核心算法——最小生成树算法(包括Prim算法和Kruskal算法)及最短路径算法(包括Dijkstra算法和Floyd算法)。此外还介绍了关键路径的概念及其在AOE网络中的应用,并简要比较了DFS与BFS算法。

















 921
921

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










