图论-最小生成树以及最大关键路径

①定义
最小生成树：针对一个图，使所有节点都连接在一起，需要n-1条边（n为节点），并且所有的边权和为最小的，故连接该n个节点+(n-1)条边为该图的最小生成树。

从而得，一个图如果有最小生成树，则改图一定是联通的

②实现算法
最小生成树的生成算法:
1，Prim算法
该算法类似于dijkstra算法，区别在于dijkstra算法通过vis[]数组中的值是否为1或者0，来保存是否存储过，
而prim算法，使用dist[]距离数组来存储，若dis为0则，该节点已经被选取。
讲到这里，先说一下Prim的原理：

过程：
1.选区任意一个源节点(对最小生成树的构建不会造成影响)
2.将该节点作为一个集合(该集合保存的所有点为已经被访问过的点)，找出与该集合直接相连的边权最小的节点，然后将该节点打入集合(方法：就是将源节点到该节点的距离dis更改为0)
3.类似于dijkstra算法，通过刚打入集合的节点，来修改已知的没有访问过的dis[]

具体算法实现代码如下：

const int maxn = 1e5+2;
const int INF = 100000;
int Map[maxn][maxn];
int dis[maxn];
int p[maxn]//记录前驱节点,类似于并查集中的parent数组
void Prime(int x){
    for (int i = 1; i<=n; i++){
        dis[i] = Map[x][i];        
        p[i] = i;    
    }    
    dis[x] = 0;    
    int tmp, k, ans = 0，count = 1;
    for (int i = 1;i<=n;i++){
        tmp = INF;        
        for (int j = 1; j<=n;j++){
            if(dis[j] != 0 && tmp  > dis[j]){
                 tmp = dis[j];                
                 k = j;            
             }        
         }        
         ans += dis[k];
         count++;        
         dis[k] = 0;        
         for (int j = 1; j <= n;j++){
             if(Map[k][j] != INF){
                 if(dis[j]!=0 && Map[k][j] < dis[j]){
                     dis[j] = Map[k][j];                    
                     p[j] = k;                
                 }            
             }      
          }    
      }    
      if(count != n){
       //说明不存在最小生成树，即该图是不连通的    
       }else{
          cout << ans << endl; //将最下生成树的权值和输出    
       }
   }

2.Kruskal算法
Kruskal算法是基于并查集实现的

过程:
1.将所有节点初始化，父亲节点均指向本身(并查集的初始化)
2.将所有边按照权值从小到大排序(sort)
3.从小开始遍历整个结构体数组，针对一个结构体，若边的两个节点的根节点相同，则忽略，继续遍历，，否则将该边权值记录在内

算法代码实现如下：

const int maxn = 1e5 + 2;
struct Node{
    int x;    
    int y;    
    int data;
}node[maxn];
int parent[maxn];
int n,m;
void Init(){
    for (int i = 1; i<=n; i++){
        parent[i] = i;    
    }
}
int find(int x){
    return parent[x] == x ? x : parent[x] = find(parent[x]);
}
int cmp(Node &a,Node &b){
    return a.data < b.data;
}
int main(){
    cin>>n>>m;    
    for (int i = 1; i<=m;i++){
        cin >> node[i].x >> node[i].y >> node[i].data;    
    }    
    sort(node+1,node+m+1,cmp);    
    Init();    
    int count = 1,x,y,ans = 0;    
    for (int i = 1; i<=m; i++){
         x = find(node[i].x);        
         y = find(node[i].y);        
         if(x != y){
             ans += node[i].data;            
             parent[x] = y;        
         }    
     }    
     int tmp = find(1);    
     for (int i = 2; i<=n; i++){
         if(tmp != find(i)){
             cout << "-1";            
             return 0;        
         }    
     }    
     cout << ans;    
     return 0;
 }

③最大关键路径(拓扑排序)
最大关键路径，多指一个工程，需要很多活动，并且每个活动可能存在前驱活动，即当前驱活动不全部满足的情况下，后驱活动无法执行，大概类似下图：

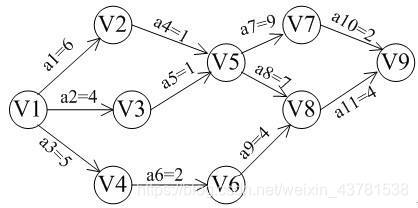
算法实现，主要是获取每个节点的入度和出度。
判断某个节点是否是关键路径上面的节点，通过earl_time[i] 是否等于late_time[i]
通过late_time[j] - earl_time[i] 是否等于 Map[i][j] ，即节点j的最晚开始时间-节点i的最早开始时间 = 节点i和节点j之间边权，即保证了节点i和节点j的自由活动时间为零
具体算法代码如下：(获取一个工程的最早完成时间)

const int maxn = 1e5+2;
const int INF = 100000;
int n,m;
int Map[maxn][maxn];
int earl_time[maxn];
int in_index[maxn]; //保存节点的入度int prev[maxn]; 
void top_sort(){
    queue<int> q; //用来保存入度为0的点    
    memset(earl_time, 0, sizeof(earl_time));    
    for (int i = 1; i<=n; i++){
        if(in_index[y] == 0)            
        q.push(y);    
    }    
    int tmp,count =0;    
    while(!q.empty()){
        tmp = q.front();        
        q.pop();        
        count++;        
        for (int i = 1; i<=n; i++){
            if(Map[tmp][i] != INF){
                if(earl[tmp] + Map[tmp][i] > earl_time[i]){
                     arl_time[i] = earl[tmp] + Map[tmp][i];
                }                
                if(--in_index[i] == 0){                    
                    q.push(i);                
                }            
            }        
        }    
    }    
    if(count != n){
        cout << "0"; //代表该工程无法完成    
    }else{
        int ans = 0;        
        for (int i = 1;i<=n; i++){
            ans = max(ans, earl_time[i]);        
        }        
    cout << ans; //将该工程需要消耗最小时间输出    
    }
}
int main(){
    cin>>n>>m;    
    for (int i = 1; i<=n; i++){
        for (int j = 1; j <= n;j++){
            Map[i][j] = INF;
         }    
    }    
    int x, y, len;    
    for (int i = 1; i<=m; i++){
        cin>>x>>y>>len;        
        Map[x][y] = len;//有向图        
        in_index[y]++;    
    }    
    top_sort();    
return 0;
}

最后，late_time[] 最晚完成时间的获取，与earl_time[]的获取类似，
不同点在下：

while(!q.empty()){
    tmp = q.front();    
    q.pop();    
    count++;    
    for (int i = n; i>=1; i--){ //由于出度为0的点，在工程最后，所以遍历方向是从尾到头        
        if(Map[i][tmp] != INF){
            if(late_time[i] > late_time[tmp] - Map[i][tmp]){
                late_time[i] = late_time[tmp] - Map[i][tmp];
            }            
            if(--out_index[i] == 0){ //out_index为保存出度的数组,                
                q.push(i);            
            }        
        }    
    }
}

故获取完所有活动的最早开始时间earl_time[]和最晚开始时间late_time[]，故关键路径获取如下:

for (int i = 1; i<=n;i++){
    if(earl_time[i] != late_time[i]){
        continue;    
    }    
    for (int j = n; j >= 1; j--){
        if(Map[i][j] != INF && earl_time[j] = late_time[j] && (late_time[j] - earl_time[i] == Map[i][j])){
             printf("%d->%d\n", i, j);        
         }    
     }
}