牛牛的数列 (可修改的连续上升子序列)

题目描述

牛牛现在有一个n个数组成的数列,牛牛现在想取一个连续的子序列,并且这个子序列还必须得满足:最多只改变一个数,就可以使得这个连续的子序列是一个严格上升的子序列,牛牛想知道这个连续子序列最长的长度是多少。

输入格式

输入包括两行,第一行包括一个整数n(1 ≤ n ≤ 10^5),即数列的长度;
第二行n个整数a_i, 表示数列中的每个数(1 ≤ a_i ≤ 10^9),以空格分割。

输出格式

输出一个整数,表示最长的长度。

输入样例

6 
7 2 3 1 5 6

输出样例

5

---

分析

本题所求的是连续的最大长度，因为可以修改一个数据已达到长度最大的效果，假如修改第k个数

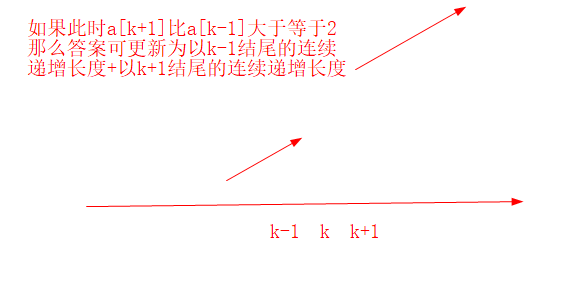
如果第k-1个数比第k+1个数小于等于2，那么就可以把第k个数修改进而生成更长的连续上升子序列。

所以求一个数组l[]记录以第i个数结尾的连续上升子序列长度
求一个数组r[]记录以第i个数开头的连续上升子序列长度

最后求l[i-1]+r[i+1]+1的最大值

C++ 代码

#include<bits/stdc++.h>
using namespace std;
const int N = 1e5+10;
int n,a[N],l[N],r[N],ans;
int main()
{
	ios::sync_with_stdio(false);
	cin>>n;
	for(int i=1;i<=n;i++) cin>>a[i];
	for(int i=1;i<=n;i++)   //第i个数结尾的连续上升子序列长度
	{
		if(a[i]>a[i-1]) l[i]=l[i-1]+1;
		else l[i]=1;
	}
	for(int i=n;i>0;i--)    //第i个数开始的连续上升子序列长度
	{
		if(a[i]<a[i+1]) r[i]=r[i+1]+1;
		else r[i]=1;
	}
	for(int i=1;i<=n;i++)
	{
		if(a[i+1]>=a[i-1]+2)    
		{
			ans=max(ans,l[i-1]+r[i+1]+1);
		}
	}
	cout<<ans;
	return 0;
}