Dijkstra 算法-利用Indexed Priority Queue实现

Jasonchen1224

已于 2023-02-11 11:36:46 修改

阅读量184

点赞数 1

CC 4.0 BY-SA版权

文章标签：算法数据结构 c++

于 2023-02-11 11:36:37 首次发布

本文链接：https://blog.youkuaiyun.com/Jasonchen1224/article/details/128981660

本文介绍了Eager方式的Dijkstra算法，与Lazy方法的区别在于找到更短路径时直接更新节点，而非重复插入。通过索引优先队列（IPQ）实现，提高效率，避免资源浪费。在给定的图示例中，展示了如何使用IPQ更新节点距离并优化程序性能。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

索引优先队列回顾
我们在之前的博文中提到索引优先队列中提到，利用索引优先队列可以容易利用contains函数实现查找，利用Decrease_Valueof函数更新已有节点的最小距离，此函数避免重复插入记录，造成后续重复记录占用程序资源和时间。当让也需要利用常规的insert 和 poll函数，对队列进行基本的操作。建议阅读本博文之前，先行乐队上述链接。
Eager方式的Dijkstra算法
Eager方式和Lazy方式的最大区别是，lazy只是不加选择的插入，Eager对于重复节点，如果找到更短距离，那么直接进行更新，无需插入
我们利用William 提供的材料进行说明
下图1 当中，我们已经检查完成节点4,更新节点4的dist值为13，然后我们检查节点1的dist值，我们发现，通过节点2后，节点1的距离可以减少到(4)，这时我们有两个选择，选择之一为之前的lazy模式，直接插入，本文利用IPQ，直接更新节点1.

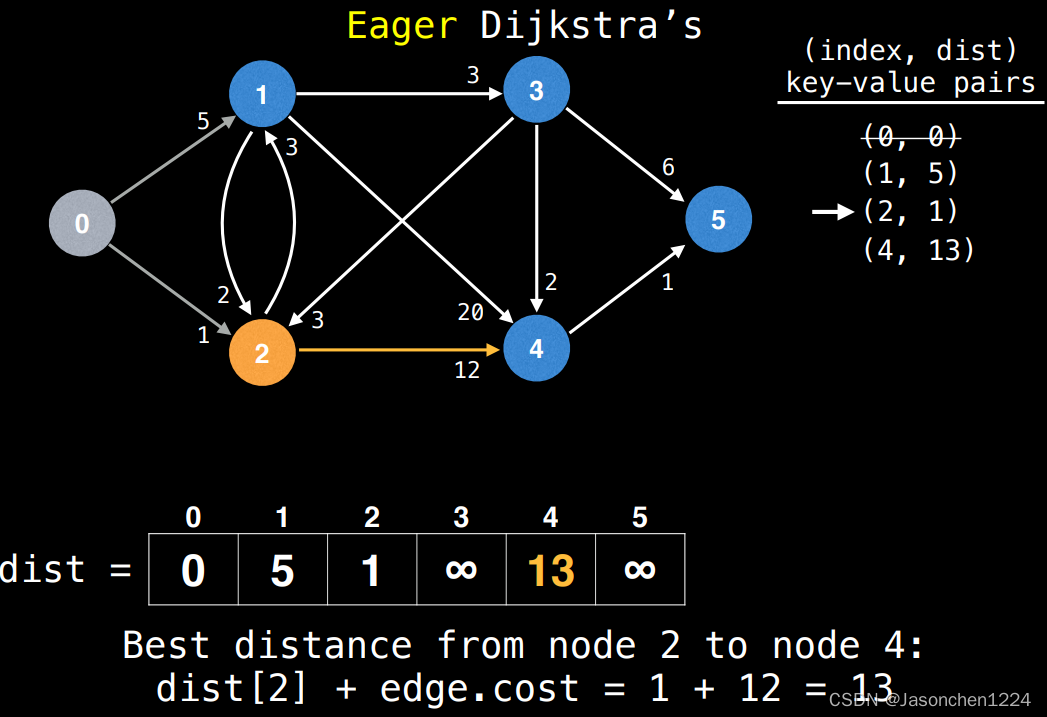
更新节点1的dist示意，利用更新，我们可以提升程序效率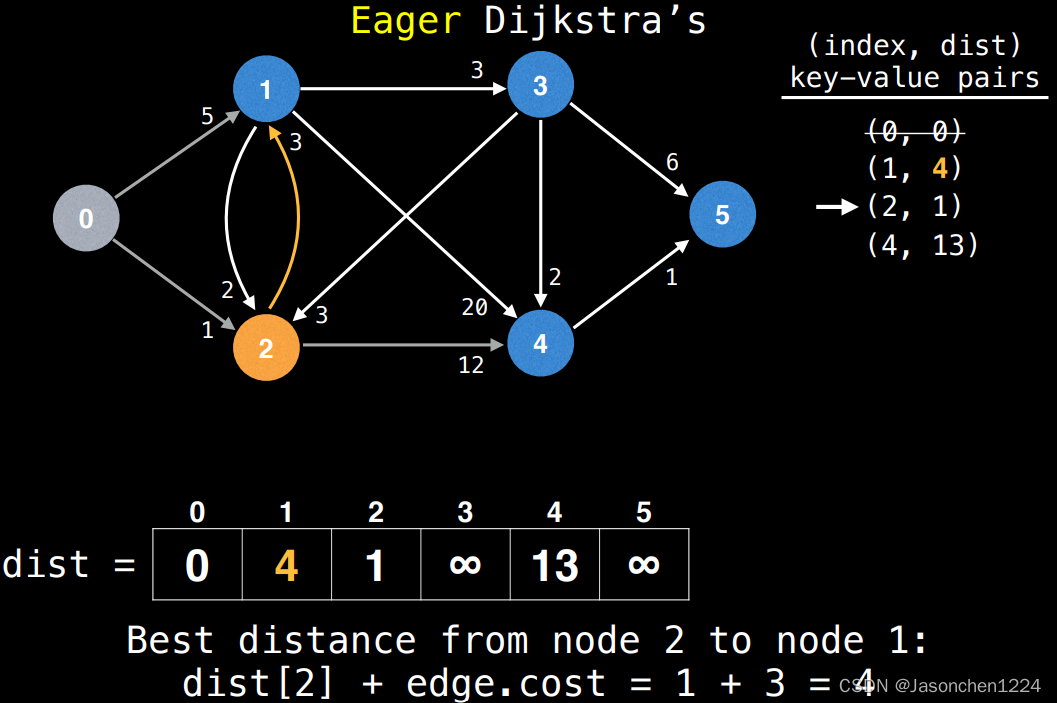
代码实现（部分)，其余代码参考前一篇博客, Lazy算法

void Dijkstra_Eager(ALGraph G, int s, int *dist, int *prev)
{
    int i;
    int v;
    int w;
    int minvalue;
    ArcNode *p;
    IPQ_Node ipq;

    Init_IPQ(&ipq);

    for(i=0;i<G.vexnum;i++)
    {
        *(prev+i)=-1;
        *(dist+i)=INT_MAX;
        visited[i]=0;
    }

    dist[s]=0;
    Insert_KeyValue(&ipq,s,0); // insert keyindex + value

    while(ipq.sz>0)
    {
        v=Peek_MinKeyIndex(ipq);
        minvalue=Poll_MinValue(&ipq);

        visited[v]=1;

        if(dist[v]<minvalue)
        {
            continue;
        }
        for(p=G.vertices[v].firstarc;p;p=p->nextarc)
        {
            w=p->adjvex;

            if(!visited[w])
            {
                if((dist[v]+*(p->info)) < dist[w])
                {
                    dist[w] = dist[v] + *(p->info);
                    prev[w]=v;

                    if(!contains(ipq,w))
                    {
                        Insert_KeyValue(&ipq, w, (dist[v] + *(p->info)));
                    }
                    else
                    {
                        Decrease_Valueof(&ipq, w, (dist[v] + *(p->info)));
                    }
                }
            }
        }
    }

}