线性回归——最小二乘法（一）

目标：本文详细将讲解单变量线性回归并写出使用最小二乘法（least squares method）来求线性回归损失函数最优解的完整过程，首先推导出最小二乘法，后用最小二乘法对一个简单数据集进行线性回归拟合；

线性回归

　　线性回归假设数据集中特征与结果存在着线性关系；

　　等式：y = mx + c

　　y为结果，x为特征，m为系数，c为误差 在数学中m为梯度c为截距

　　这个等式为我们假设的，我们需要找到m、c使得mx+c得到的结果与真实的y误差最小，这里使用平方差来衡量估计值与真实值得误差（如果只用差值就可能会存在负数）； 用于计算真实值与预测值的误差的函数称为：平方损失函数（squard loss function）；这里用L表示损失函数，所以有：

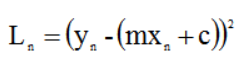
整个数据集上的平均损失为：

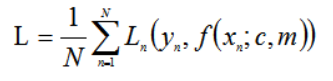
我们要求得最匹配的m与c使得L最小；数学表达式可以表示为：

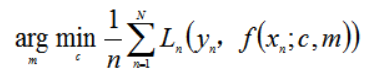
最小二乘法用于求目标函数的最优值，它通过最小化误差的平方和寻找匹配项所以又称为：最小平方法；这里将用最小二乘法用于求得线性回归的最优解；

最小二乘法

　　为了方便讲清楚最小二乘法推导过程这里使用，数据集有1…N个数据组成，每个数据由、构成，x表示特征，y为结果；这里将线性回归模型定义为：

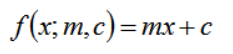
平均损失函数定义有：

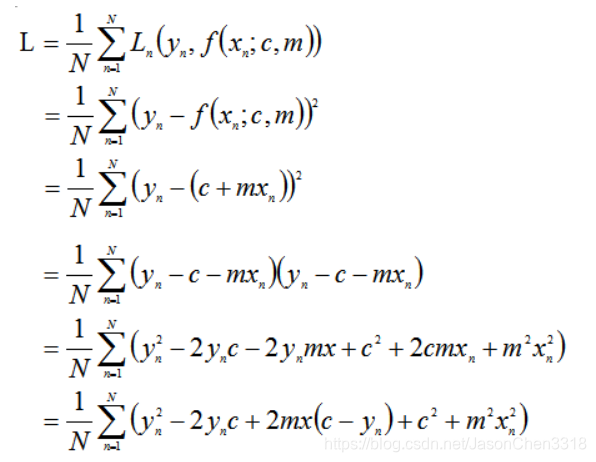
要求得L的最小，其关于c与m的偏导数定为0，所以求偏导数，得出后让导数等于0，并对c与m求解便能得到最小的L此时的c与m便是最匹配该模型的；

关于c偏导数：

因为求得是关于c的偏导数，因此把L的等式中不包含c的项去掉得：

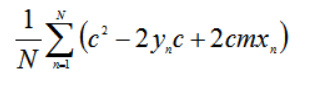
整理式子把不包含下标n的往累加和外移得到：

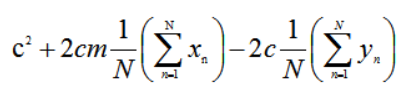
对c求偏导数得：

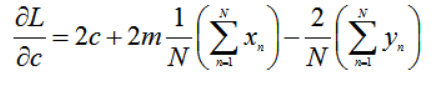
关于m的偏导数：

求关于m的偏导数，因此把L等式中不包含项去掉得：

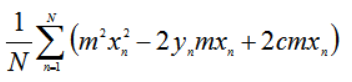
整理式子把不包含下标n的往累加和外移得到：

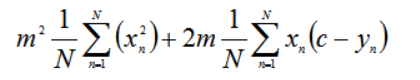
对m求偏导数得：

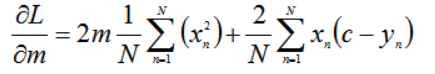
令关于c的偏导数等于0，求解：

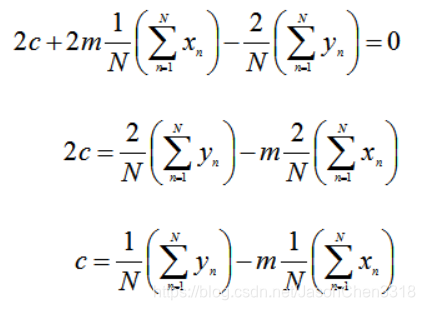
从上求解得到的值可以看出，上面式子中存在两个平均值，因此该等式也可以改写成：

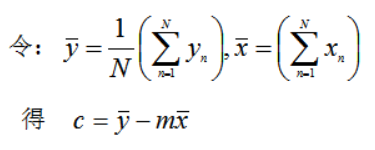
令关于m的偏导数等于0，求解：
　　关于m的偏导数依赖于c，又因为已经求得了关于c偏导数的解，因此把求关于c偏导数的解代数关于m的偏导数式子得：

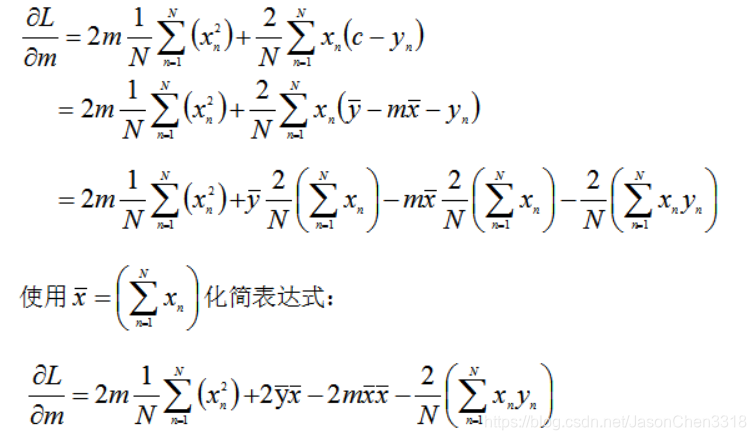
合并含有m的项化简：

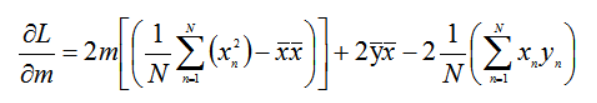
求解：

 

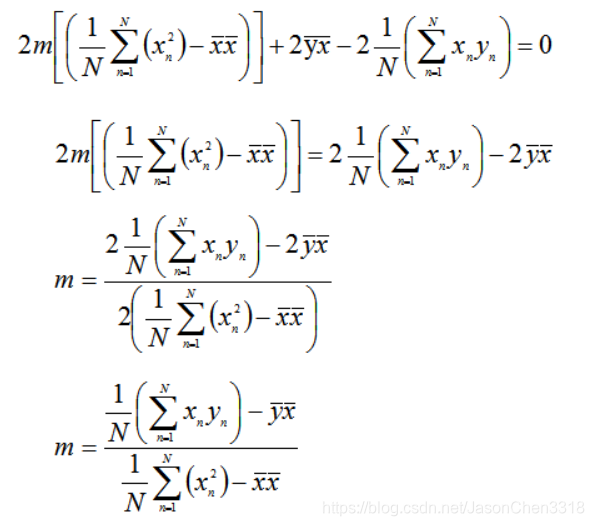
为了简化式子，再定义出：

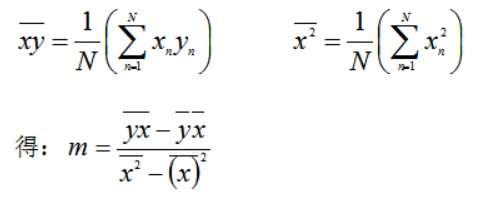
示例：

这里使用上面得到的最小二乘法公式对以下数据集进行线性拟合：

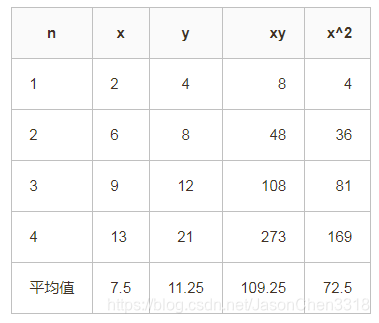
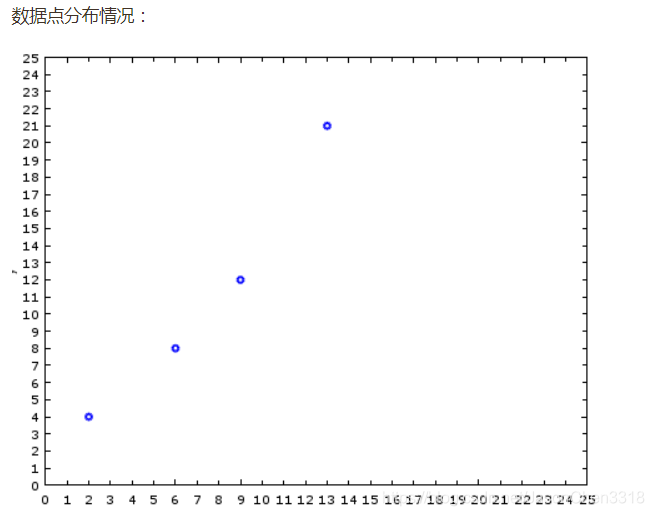
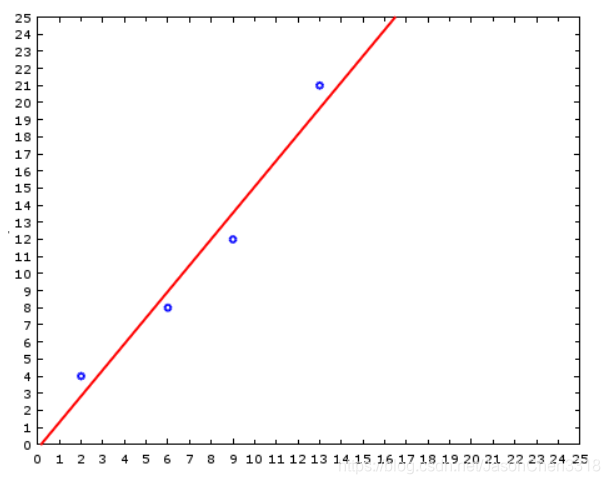
最后得出当前线性函数为：

y = 1.5307x - 0.23

计算出每个节点的预测值：

y1 = 1.5307 * 2 - 0.23 = 2.83
y2 = 1.5307 * 6 - 0.23 = 8.9542
y3 = 1.5307 * 9 - 0.23 = 13.5463
y4 = 1.5307 * 13- 0.23 = 19.6691

拟合结果：

 

线性回归——最小二乘法（一）