数据结构算法——1042. 字符串模式匹配KMP算法

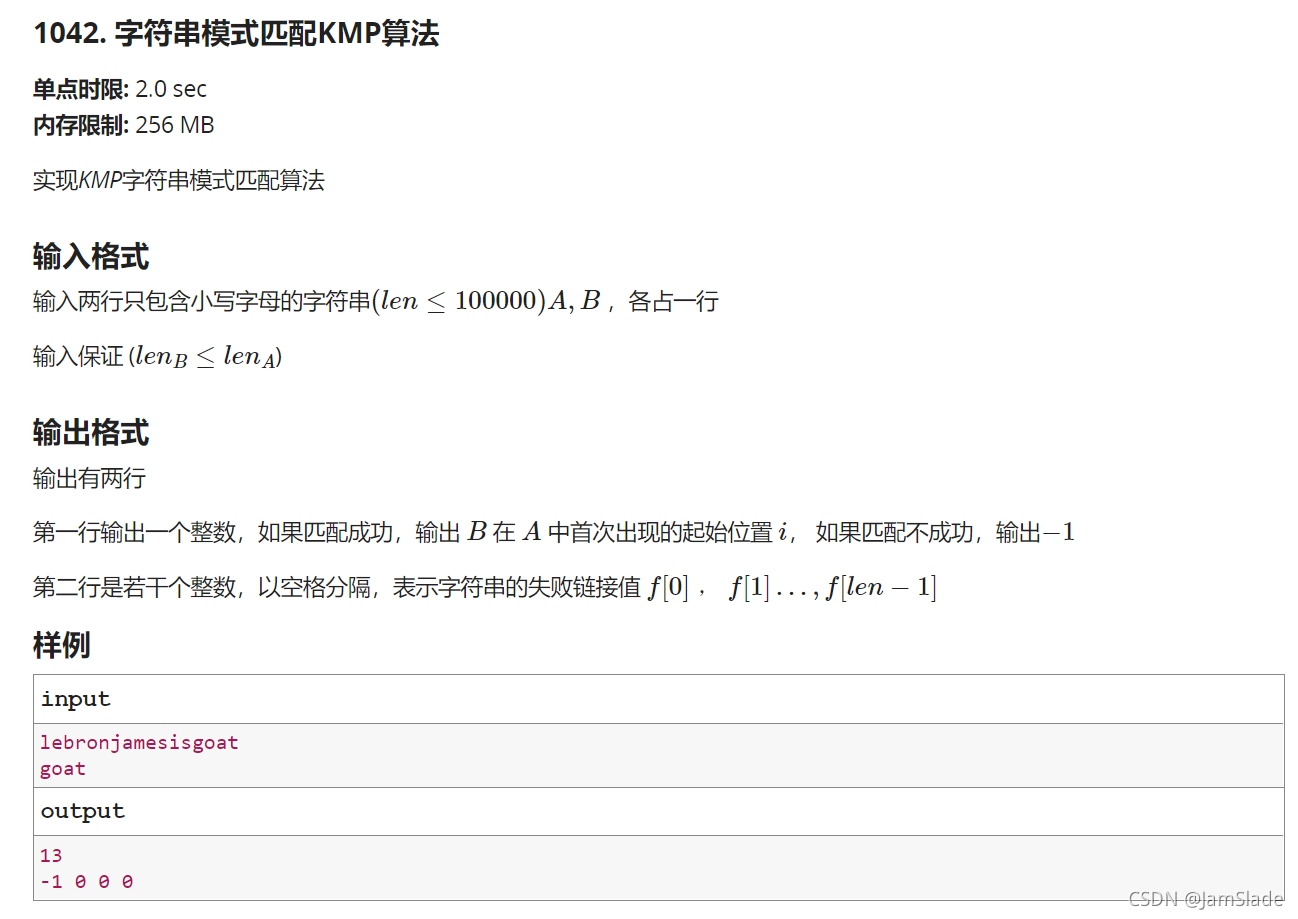
题目

在这里插入图片描述

思路

把next数组求出来

举个例子

![在这里插入图片描述](https://img-blog.csdnimg.cn/5c94e122d0384afaaa021e1ff505e7da.png

当我们程序在判断2字符串最后一个a和1字符串的子串不匹配的时候，我们其实根本没必要再去判断中间的a是否需要
我们直接把后续整个部分都移动到a后面即可，那么问题来了，移动几个a呢？
在这个题目中，应该是移动成这种情况
在这里插入图片描述
将第一个a放到不匹配的区域
（如果不理解再举个例子
这里不匹配的是a和f，那么我们应该找8字符串的f前面的c来判断要移动多少步，如果直接移动6步，就会缺失掉移动三步时候刚好匹配的情况

如何找短的字符串每个位置对应移动的步数？

这时候我们需要观察字符串的情况了
拿第二个举例子
当f出现匹配失误的时候，我们就得看前面abcabc的部分来看“后缀”和“前缀”是否一样
在这里插入图片描述
不难发现当长度为3的时候，前缀和后缀是一样的，这个时候，我们要往后移动6-3=3步，保证你下一次匹配的时候，abc这部分仍然可以匹配上前面部分的abc,此时从第四个位置a开始一一比对

(长度为6的子集必定相等，这个时候是移动6-6=0步，没有意义）

所以我们很容易得出子串每个位置对应的next比对内容
（注意：若为i匹配不上，下一个匹配的是next[i-1],也就是i-1的数字对应的前后缀)

“” 当第一个字符不匹配，我们默认为-1（也可以是0，只是差一个数字罢了）
a，公共前后缀是他自身，往后移动 1 - 0 = 1步，光标移动到a上为 0
ab, 公共前后缀只有2（本身），所以我们可以认为没有公共前后缀，移动的大小为 2 - 0 = 2步，在程序上就是把比对的光标移到a上为 0
abc 同上，移动 3 - 0 = 3,把光标移动到a上 0
abca 前后缀最大为1（把等于本身的去掉），所以移动 4 - 1 = 3步，把光标移动到b 1
abcab 前后缀最大为2，所以移动 5 - 2 = 3步，把光标移动到c 2
abcabc 前后缀最大为 3，移动 6 - 3 = 3 步，光标移动到c
于是我们得到如下表格
在这里插入图片描述、
得到next数组代码

int getIn(string a, string b)
{
    int bl = b.length();
    //获取next数组部分
    int i = 0, j = -1;
    int* next = new int[b.length() + 10];
    memset(next, 0 ,sizeof(next));
    next[0] = -1;
    while(i < b.length())
    {
        if(j == -1 || b[i] == b[j])
        {
            i++;j++;
            next[i] = j;
        }
        else
        {
            j = next[j];//下标变回0，也就把前面所有部分都移动
        }
    }
}

找寻KMP匹配的代码

int firIn(string a, string b, int* next)
{
    int i = 0, j = 0;
    int al = a.length(), bl = b.length();
    while(i < al && j < bl)
    {
        if(j == -1 || a[i] == b[j])
        {
            i++;j++;
        }
        else
            j = next[j];
			//短串右移等于长串左移，相对运动
			//这里的j是递归的找前面子串匹配的字符，一直不匹配才回到0
    }

    if(j >= bl)
        return i - bl;
    else return -1;
}

解释一下 j = next[j]的部分

构造一个子串 AAEAAPOPOAAEAAE
当我们在最末尾巴的E不匹配的时候
第一次j = next[j]
在这里插入图片描述
我们就会看最长前缀和最长后缀来进行分析
然后发现我们
在检验AAEAA这一部分的时候

前面的AAEAA后一个字符是P
而后缀字符是E
也不匹配
这个时候我们再次 j = next[j]
此时代表的意思是从AAEAA这个子串入手，不难发现最长和前后缀都是AA
在这里插入图片描述
于是我们从AAEAA再回溯到AA
发现开头的AA后面接着是E
恰好匹配你后缀后续的E

代码

#include<iostream>
#include<string.h>
using namespace std;

int main()
{
    string a,b;
    cin >> a >> b;


    //获取next数组部分
    int j = 0, k = -1;
    int al = a.length(); int bl = b.length();

    int* next = new int[bl + 10];
    memset(next, 0 ,sizeof(next));


    next[0] = -1;
    while(j < bl)
    {
        if(k == -1 || b[j] == b[k])
        {
            j++;k++;
            next[j] = k;
        }
        else
        {
            k = next[k];//变回0
        }
    }

    //找寻字符串部分
    int i = 0; j = 0;
    while(i < al && j < bl)
    {
        if(j == -1 || a[i] == b[j])
        {
            i++;j++;
        }
        else
            j = next[j];
    }
    
    //cout
    if(j >= bl)
        cout << i - bl << endl;
    else cout << "-1" << endl;


    for(i = 0; i < bl; i++)
        cout << next[i] << ((i == bl - 1) ? "" : " ");//
    cout << endl;
}