[課程筆記] 機器學習基石 - W4. Feasibility of Learning

傷心太平洋

已于 2022-09-15 09:37:12 修改

阅读量424

点赞数

CC 4.0 BY-SA版权

分类专栏：機器學習基石文章标签：机器学习

于 2022-03-26 23:56:25 首次发布

版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。

本文链接：https://blog.youkuaiyun.com/JYLin_master/article/details/123750479

機器學習基石专栏收录该内容

9 篇文章

订阅专栏

本文探讨了学习的可行性问题，通过概率论和统计方法解释为何学习是可能的。文章以简单的图像分类为例，讨论了不同假设函数的表现，并引入了Hoeffding不等式来量化抽样误差的概率。最终通过统计学习流程说明了如何从众多假设中选择最优模型。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

目录

Video1: Learning is Impossible

Two Controversial Answer

Video2: Probability to the Rescue

Inferring Something Unknown

Hoeffding's Inequality

Video3: Connection to Learning

Connection to Learning

Added Component

Verification Flow

Video4: Connection to Real Learning

Bad Sample and Bad Data

The Statistical Learning Flow

Video1: Learning is Impossible

Two Controversial Answer

以简单的图像分类为例，即使透过数据集Ｄ (6 个图像以及答案) 学到了一些规则
- 规则A: 对称图像 = +1, 其他 = -1
- 规则B: 左上角点是黑色 = -1, 其他 = +1
使用学到的规则来预测数据集外的图像，仍然可能会预测错误
- 使用规则A 预测 ----> 正确答案可能是规则B
- 使用规则B 预测 ----> 正确答案可能是规则A
这是否意味着，学习是无用的? (因为即使用数据集D训练过，对于D以外的数据模型仍会答错)

No Free Lunch

再以一个分类问题为例:
- 输入是 3 个 bits，输出是 1 个 bit
- 考虑所有可能的输入输出，可知 hypothesis, H 中有 $2^8$ 种可能的函数
- 从 H 挑选出最佳的 g ，使得 f 与 g 在数据集 D 上的表现相同
- 这样的 g 到底是好还是不好?
No free lunch
- 如果任何的 f 都可能出现，则从数据 D 学习预测 D 以外的数据，是会失败的

Video2: Probability to the Rescue

Inferring Something Unknown

透过某些操作，我们可以从未知的事物得到一些线索
以推测瓶中的橘色弹珠比例为例，可以透过取样的结果来估算
虽然取样出的比例并不一定等于瓶中的比例，但至少有很大的几率会是接近的

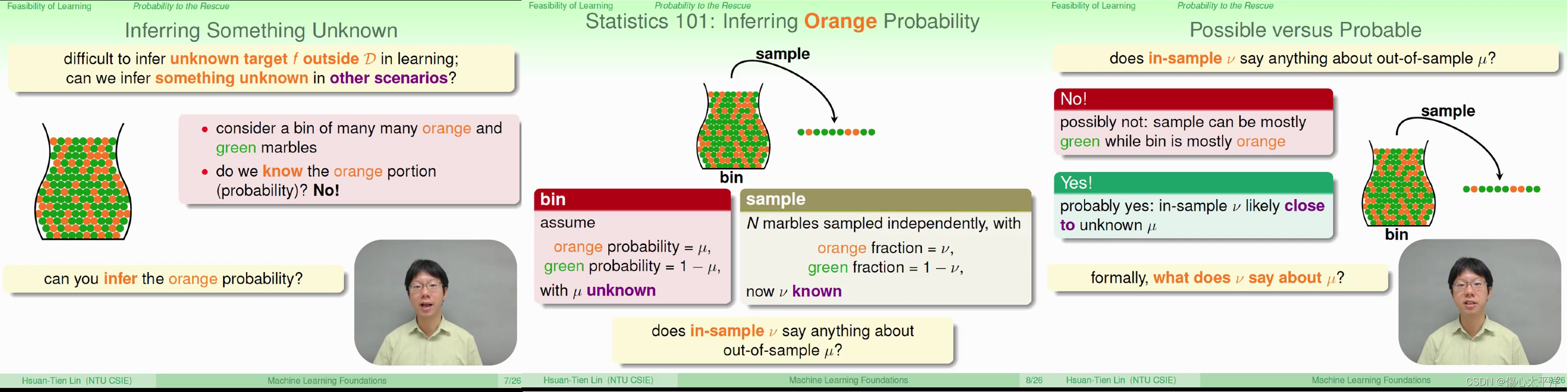
Hoeffding's Inequality

抽样结果的误差超出容忍值的几率，会随着取样数的增加而降低

Video3: Connection to Learning

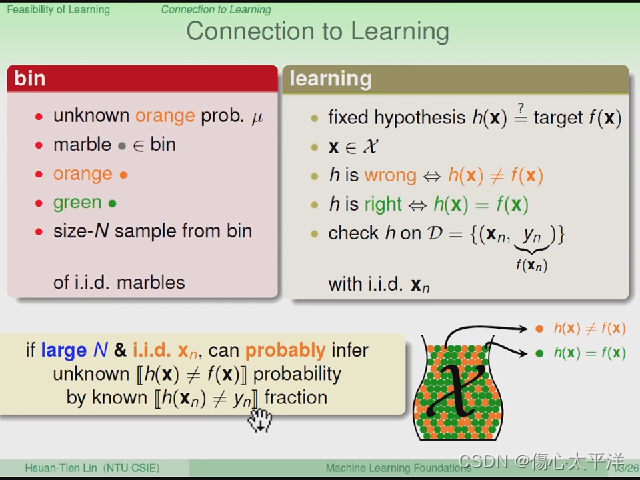
Connection to Learning

将前面抽弹珠的故事与机器学习做对比:
- 抽弹珠
  - 未知: 橘色比例
  - 抽样: 得到橘色、绿色的比例
  - 当抽样数量很大时，抽样的结果会接近实际上的 [ 橘色比例 ]
- 机器学习
  - 未知: f(x)≠h(x)比例
  - 抽样: 得到 f(x)≠h(x) 、f(x)=h(x) 的比例
  - 当抽样数量很大时，抽样的结果会接近实际上的 [ f(x)≠h(x)比例 ]
此处 h 指的是 H 中的一个函数，g 指的是演算法最后选出的函数

Added Component

在原本的流程中，加入一个取样的过程 P ，用于两个地方:
- 取出数据集 D ，用来训练模型
- 取出数据集 D ，用来评估 h 与 f 是否相近
透过模型在数据集 D 的表现( $E_{in}$ )，可以评估模型在数据集 D 以外的表现( $E_{out}$ )

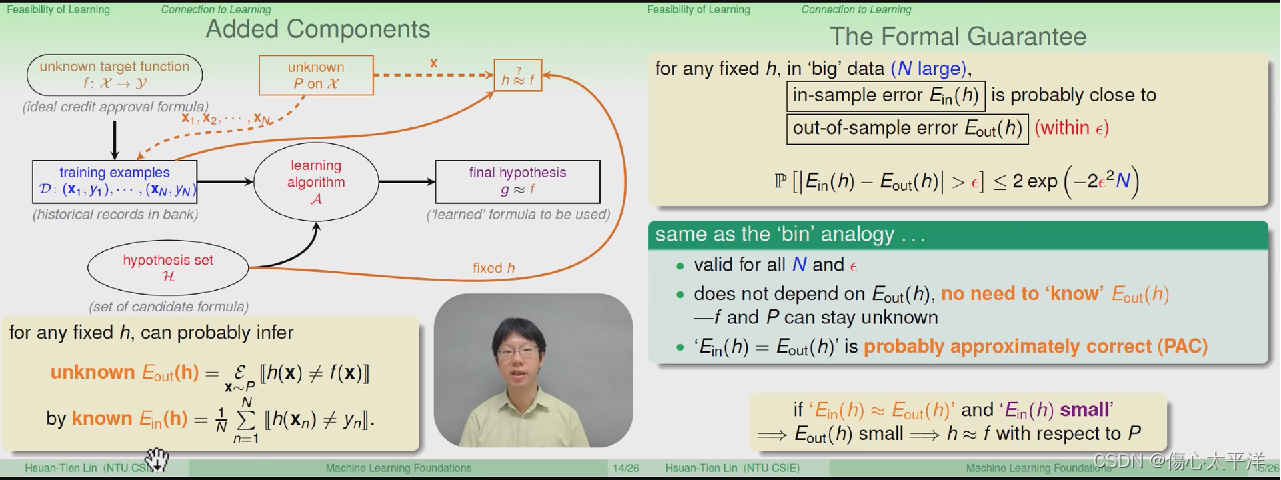
Verification Flow

即使我们能估算模型在数据集 D 以外的表现( $E_{out}$ )，仍不能说这是个良好的学习过程
这个步骤只能称为是验证，用来验证手上的一个 h 是好还是坏
良好的学习过程必须要有:
- 演算法能有多样的选择，从 H 中取出多个 h
- 能评估 h 的好坏
- 最后挑选出一个好的 g

Video4: Connection to Real Learning

Multiple h

另一个问题是，透过验证的方式真的能选到最佳的 g 吗?
当我们有许多可选择的 h ，很有可能会发生 $E_{in}$ 偏离 $E_{out}$ 的情况
以抽弹珠为例，即使橘色与绿色各占一半，仍有可能在一次抽样中得到全部都是绿色的结果
以丢硬币为例，请全班 150 人，每个人丢 5 次硬币，其中至少出现一次五次正面的几率是大于 99% 的
这表示当存在多个 h 可选择时，可能会得到不好的 g

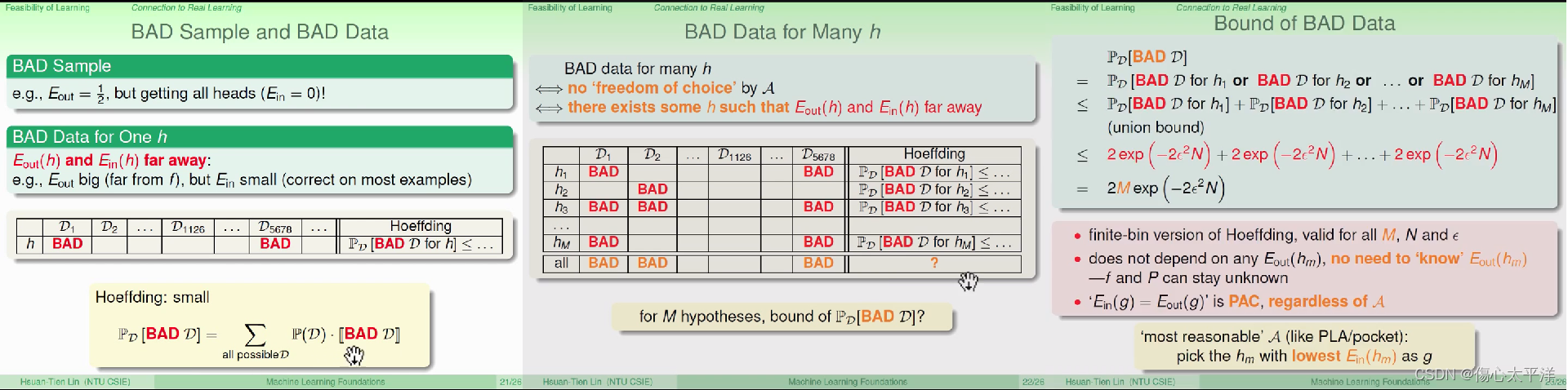
Bad Sample and Bad Data

不好的取样与不好的数据:
- 透过取样数据 D ，得出的 $E_{in}$ 与 $E_{out}$ 差异很大
当只有一个 h 时，bad data 产生的影响
- 根据 Hoeffding's Inequality ，当样本数量很大时， $E_{in}$ 有很大的几率会接近 $E_{out}$
- 在多次抽样下，得到许多不同的 D，大部分的 D 得到的 $E_{in}$ 会很接近 $E_{out}$
- 结论是影响很小，因为抽出 bad data 几率很低
当有 M 个 h 可选择时，bad data 产生的影响
- 当 h 的选择变多时，不好的采样更容易出现 (只要对任一 h 不好，就视为不好的采样)
- 根据 Hoeffding's Inequality ，可知抽到 bad data 几率与 H 的大小 M 、样本数 N 有关
- 结论是若 M 是有限的，则影响很小，因为抽出 bad data 几率同样很低

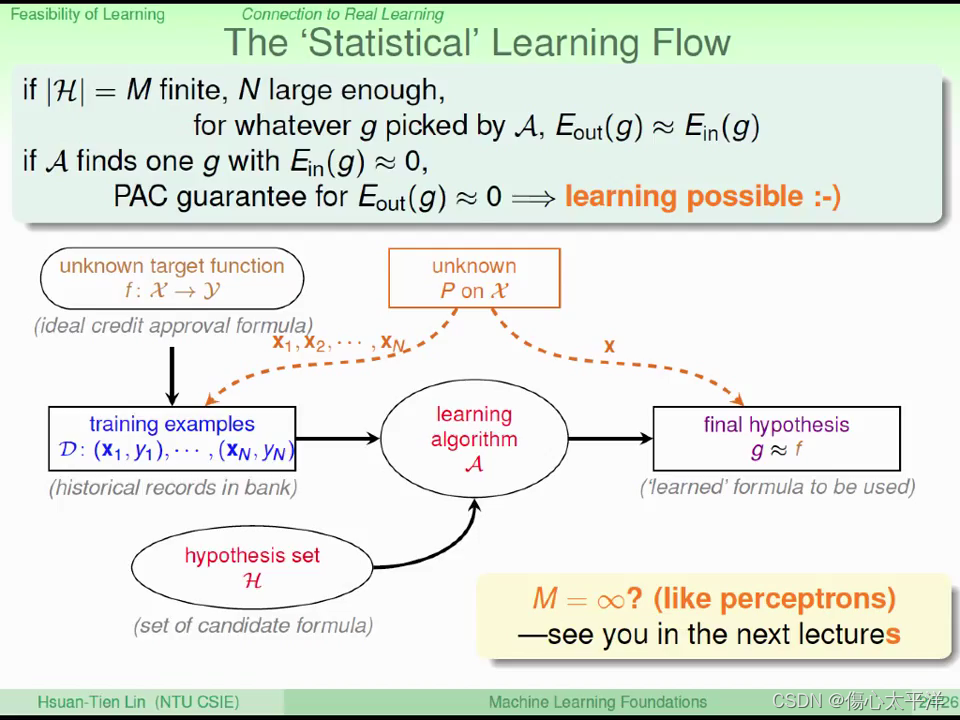
The Statistical Learning Flow

当 M 的数量是有限的，且抽样的数量够大时， $E_{in}$ 会很接近 $E_{out}$
当我们能透过 $E_{in}$ ，大概的估算出 $E_{out}$ ，则可以挑选一个 $E_{in}$ 最小的 g
因此学习是可行的

参考

機器學習基石上 (Machine Learning Foundations)---Mathematical Foundations | Coursera

评论

被折叠的条评论为什么被折叠?

到【灌水乐园】发言

查看更多评论

添加红包

成就一亿技术人!

hope_wisdom

发出的红包

实付元

使用余额支付

点击重新获取

扫码支付

钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。