Vision Transformer（学习自用）

最新推荐文章于 2025-05-17 08:00:00 发布

JJxXxLL

最新推荐文章于 2025-05-17 08:00:00 发布

阅读量1.8k

点赞数 56

CC 4.0 BY-SA版权

文章标签： transformer 学习深度学习

本文链接：https://blog.youkuaiyun.com/JXLLLLLLLLLLLLLL/article/details/140197707

参考资源：

前言

背景与动机
背景：Transformers 在自然语言处理（NLP）任务中表现出色，并成为主流模型。受此启发，研究人员尝试将其应用于计算机视觉任务。
动机：传统的视觉任务主要依赖于卷积神经网络，而 Transformers 主要用于替代部分卷积层或增强特征表示。本文探讨了完全基于 Transformers 的模型在图像分类中的表现。

图示结构

Vision Transformer (ViT) 结构

图像划分为补丁：将输入图像划分为固定大小的补丁（如16x16），然后将这些补丁展平并线性嵌入到特定维度。
位置嵌入：为了保留位置信息，将可学习的位置嵌入添加到每个补丁嵌入中。
Transformer 编码器：将这些嵌入作为序列输入到标准的 Transformer 编码器中，编码器由多层多头自注意力和前馈神经网络组成。
分类标记：在输入序列的开头添加一个可学习的分类标记，其最终的表示用于图像分类。

公式表示结构

在这里插入图片描述

初始输入表示

$\mathbf{z}_0$ = [ $\mathbf{x}_{\text{class}}$ ; $\mathbf{x}^1_p\mathbf{E}; \mathbf{x}^2_p\mathbf{E}$ ; $\cdots$ ; $\mathbf{x}^N_p\mathbf{E}]$ + $\mathbf{E}_{\text{pos}}$

$\mathbf{x}_{\text{class}}$ ：分类标记（classification token）
$\mathbf{x}^i_p$ ：第 $i$ 个补丁（patch）的展平向量
$\mathbf{E}$ ：线性变换矩阵，将补丁向量映射到嵌入空间
$\mathbf{E}_{\text{pos}}$ ：位置嵌入，用于保留每个补丁的位置信息
$\mathbf{z}_0$ ：初始嵌入表示，包含分类标记和所有补丁的嵌入表示以及位置嵌入的和

多头自注意力层

$\mathbf{z}'_{\ell}$ = $\text{MSA}(\text{LN}(\mathbf{z}_{\ell-1}))$ + $\mathbf{z}_{\ell-1}$ , $\quad \ell = 1 \ldots L$

$\text{LN}$ ：Layer Normalization（层归一化）
$\text{MSA}$ ：Multi-Head Self-Attention（多头自注意力机制）
$\mathbf{z}_{\ell-1}$ ：前一层的输出
$\mathbf{z}'_{\ell}$ ：当前层多头自注意力后的输出，加上前一层的残差连接

前馈神经网络（MLP）层

$\mathbf{z}_{\ell}$ = $\text{MLP}(\text{LN}(\mathbf{z}'_{\ell}))$ + $\mathbf{z}'_{\ell}$ , $\quad \ell = 1 \ldots L$

$\text{MLP}$ ：包含两层线性变换和一个 GELU 非线性激活函数的前馈神经网络
$\mathbf{z}'_{\ell}$ ：当前层多头自注意力后的输出
$\mathbf{z}_{\ell}$ ：当前层前馈神经网络后的输出，加上多头自注意力层的残差连接

最终输出表示

$\mathbf{y}$ = $\text{LN}(\mathbf{z}^0_L)$

$\text{LN}$ ：Layer Normalization（层归一化）
$\mathbf{z}^0_L$ ：第 $L$ 层的分类标记输出

各模块介绍

初始输入

分类标记的作用
分类标记的引入源自 Transformer 架构中用于分类任务的一个设计。在某些模型（例如 Vision Transformer, ViT）中，输入图像被划分成多个小补丁，每个补丁被嵌入到一个向量表示中。分类标记被添加到补丁序列的前面，其作用是聚合来自所有补丁的信息，并用于最终的分类任务。

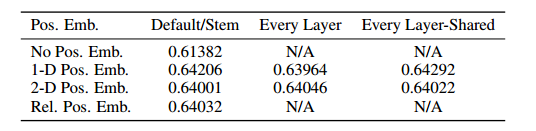
位置嵌入目的
在图像处理的 Transformer 模型（如 Vision Transformer, ViT）中，位置嵌入（positional embeddings）用于保留输入图像中每个补丁的位置信息。因为 Transformer 模型本身不具备位置信息，所以需要显式地将这些信息添加到输入中。使用二维感知嵌入未能显著提高性能，所以使用一维。

self.positions = nn.Parameter(torch.randn((img_size // patch_size) ** 2 + 1, emb_size))
"""
img_size // patch_size 计算图像在每个维度上被划分成的补丁数。
(img_size // patch_size) ** 2 计算总的补丁数。
+ 1 用于包含分类标记（classification token）的嵌入。
emb_size 是嵌入向量的维度。
"""

一维原因

图像分割和补丁嵌入

在 ViT 模型中，输入图像首先被划分为多个固定大小的补丁（patch），例如每个补丁的大小为 16x16。每个补丁被展平为一个一维向量，并通过一个线性变换（全连接层）转换为一个高维嵌入向量。
线性变换（全连接层）：假设输入图像的大小为 224x224，划分为 16x16 的补丁，则总共会有 (224 / 16) * (224 / 16) = 14 * 14 = 196 个补丁。每个补丁的像素数为 16 * 16 = 256，如果输入图像是 RGB 图像，则每个补丁的维度为 256 * 3 = 768。
嵌入维度的选择：通过线性变换，将每个补丁的展平向量转换为一个固定大小的嵌入向量。这个固定大小的嵌入维度通常设置为 768。选择 768 作为嵌入维度是一个经验性的选择，通常在实际应用中，嵌入维度的大小可以根据具体的任务和数据集进行调整。例如，可以选择 512、768、1024 等不同的嵌入维度。

嵌入维度的作用：

高维嵌入向量能够捕捉更多的特征和信息，有助于模型更好地表示和理解输入数据。
嵌入维度的大小直接影响模型的参数数量和计算复杂度。较大的嵌入维度通常意味着更多的参数和更高的计算复杂度，但也可能带来更好的模型性能。

掩码的作用
在多头注意力机制中，掩码的作用非常重要，特别是在处理不同长度的序列或需要忽略某些特定位置时。例如：

填充掩码（Padding Mask）：在处理不同长度的序列时，较短的序列会被填充到相同长度。填充部分不应该影响注意力权重计算，因此需要使用掩码将这些位置的注意力权重置为零。
未来信息掩码（Future Mask）：在自回归模型（如 Transformer 解码器）中，预测下一个标记时，不应看到未来的标记。未来信息掩码用于屏蔽未来位置的注意力权重。

下面给出相关代码：

class PatchEmbedding(nn.Module):
    def __init__(self, in_channels: int = 3, patch_size: int = 16, emb_size: int = 768, img_size: int = 224):
        super().__init__()
        self.patch_size = patch_size
        # 使用卷积层将图像划分为补丁并进行嵌入
        self.projection = nn.Sequential(
            nn.Conv2d(in_channels, emb_size, kernel_size=patch_size, stride=patch_size),
            Rearrange('b e (h) (w) -> b (h w) e') # 重排张量以适应 Transformer 输入
        )
        # 分类标记（可训练参数）
        self.cls_token = nn.Parameter(torch.randn(1, 1, emb_size))
        # 位置嵌入（可训练参数）
        self.positions = nn.Parameter(torch.randn((img_size // patch_size) ** 2 + 1, emb_size))

    def forward(self, x: Tensor) -> Tensor:
        b, _, _, _ = x.shape  # 提取输入张量的 batch 大小
        x = self.projection(x)  # 对输入图像进行补丁划分和嵌入
        # 重复分类标记，以适应 batch 大小
        cls_tokens = repeat(self.cls_token, '() n e -> b n e', b=b)
        # 将分类标记添加到补丁嵌入的前面
        x = torch.cat([cls_tokens, x], dim=1)
        # 添加位置嵌入
        x += self.positions
        return x

多头注意力

学到了一种新的写法：
$\color{red}{einops}$ 是一个 Python 库，它提供了一种简洁易用的方式来重新排列多维数组的形状和轴。 $\color{red}{ rearrange }$ 函数是库中用于重新排列数组轴的一个函数。它允许你以一种非常直观的方式指定新的轴顺序和大小。

输入张量x

x 的形状是 torch.Size([1, 197, 768])，
表示：1 是批次大小（batch size），197 是序列长度（sequence length）（1414+1），768 是嵌入维度（embedding dimension）（1616*3）
以下面的语句为例：

queries = rearrange(self.queries(x), "b n (h d) -> b h n d", h=self.num_heads)

self.queries(x) 的形状仍然是 (1, 197, 768)。

模式字符串 “b n (h d) -> b h n d” 解释

b 表示 batch size，对应 1。
n 表示序列长度，对应 197。
(h d) 表示嵌入维度 768 被拆分为 h 和 d，其中 h 是注意力头的数量，d 是每个头的维度。
h=self.num_heads，假设 num_heads=8。

计算每个头的维度 d

嵌入维度 768 被拆分为 8 个头，每个头 d 的维度是 768 / 8 = 96。
新形状
b 仍然是 1。
h 是注意力头的数量，对应 8。
n 仍然是序列长度，对应 197。
d 是每个头的维度，对应 96。

输出形状

rearrange 操作将输出形状为 (1, 8, 197, 96)。

这样方便后续计算。

代码如下：

class MultiHeadAttention(nn.Module):
    def __init__(self, emb_size: int = 768, num_heads: int = 8, dropout: float = 0):
        super().__init__()
        self.emb_size = emb_size
        self.num_heads = num_heads
        self.scaling = (self.emb_size // num_heads) ** -0.5
        
        # 定义线性变换层，用于生成 keys、queries 和 values
        self.keys = nn.Linear(emb_size, emb_size)
        self.queries = nn.Linear(emb_size, emb_size)
        self.values = nn.Linear(emb_size, emb_size)
        
        # 定义 dropout 层
        self.att_drop = nn.Dropout(dropout)
        
        # 定义投影层
        self.projection = nn.Linear(emb_size, emb_size)

    def forward(self, x: Tensor, mask: Tensor = None) -> Tensor:
        # 将输入 x 通过线性变换层生成 queries、keys 和 values，并拆分成多个头
        queries = rearrange(self.queries(x), "b n (h d) -> b h n d", h=self.num_heads)
        keys = rearrange(self.keys(x), "b n (h d) -> b h n d", h=self.num_heads)
        values = rearrange(self.values(x), "b n (h d) -> b h n d", h=self.num_heads)
        
        # 计算注意力能量矩阵
        energy = torch.einsum('bhqd, bhkd -> bhqk', queries, keys) # b: 批量大小, h: 头数, q: 查询长度, k: 键长度
        
        # 如果存在掩码，应用掩码
        if mask is not None:
            fill_value = torch.finfo(torch.float32).min
            energy.masked_fill_(~mask, fill_value)
        
        # 计算注意力分数并进行缩放
        att = F.softmax(energy, dim=-1) * self.scaling
        att = self.att_drop(att)
        
        # 根据注意力分数加权 values，并将结果重排回原始形状
        out = torch.einsum('bhqk, bhvd -> bhqd', att, values)
        out = rearrange(out, "b h n d -> b n (h d)")
        
        # 通过线性投影层
        out = self.projection(out)
        return out

编码器

结构图

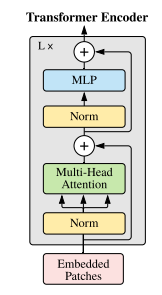
Transformer 编码器由交替的多头自注意力层（MSA，参见附录 A）和 MLP 块组成。每个块之前应用 Layernorm（LN），每个块之后应用残差连接。

残差连接块

使用ResidualAdd 类是一个用于实现残差连接（Residual Connection）的自定义 PyTorch 模块。它的目的是通过添加直接的快捷路径（shortcut path）来缓解深度神经网络训练中的梯度消失和梯度爆炸问题。这种连接方式允许信号绕过一个或多个层，从而促进信息和梯度的更好传播。

class ResidualAdd(nn.Module):
    def __init__(self, fn):
        super().__init__()
        self.fn = fn  # 将传入的函数或模块存储为类的一个属性
        
    def forward(self, x, **kwargs):
        res = x  # 保存输入 x 作为残差
        x = self.fn(x, **kwargs)  # 对输入 x 应用传入的函数或模块
        x += res  # 将残差添加回到输出
        return x  # 返回加了残差的输出

前馈神经网络模块

论文中介绍
在这里插入图片描述
使用如下代码

class FeedForwardBlock(nn.Sequential):
    def __init__(self, emb_size: int, expansion: int = 4, drop_p: float = 0.):
        super().__init__(
            nn.Linear(emb_size, expansion * emb_size),  # 第一层线性变换，将嵌入维度扩展
            nn.GELU(),  # GELU 激活函数     
            nn.Dropout(drop_p),  # Dropout 层，用于正则化
            nn.Linear(expansion * emb_size, emb_size),  # 第二层线性变换，将维度还原为原始嵌入维度
        )

expansion 参数定义了前馈神经网络中隐藏层的扩展倍数，即隐藏层的维度是输入嵌入维度的多少倍。通过设置这个参数，可以控制前馈神经网络的容量，从而影响模型的表示能力和性能。在上面的示例中，通过设置 expansion 参数，可以灵活地调整前馈神经网络块的规模。

层归一化

分类头部模块，用于将 Transformer 编码器的输出转换为最终的分类结果。这个模块包含三个主要组件：平均池化（Reduce），层归一化（LayerNorm），和全连接层（Linear）。

import torch.nn as nn
from einops.layers.torch import Reduce

class ClassificationHead(nn.Sequential):
    def __init__(self, emb_size: int = 768, n_classes: int = 1000):
        super().__init__(
            Reduce('b n e -> b e', reduction='mean'),  # 平均池化
            nn.LayerNorm(emb_size),  # 层归一化
            nn.Linear(emb_size, n_classes)  # 全连接层输出类别
        )

残差连接模块

对应多头注意力层和前馈神经网络层

$\mathbf{z}'_{\ell}$ = $\text{MSA}(\text{LN}(\mathbf{z}_{\ell-1}))$ + $\mathbf{z}_{\ell-1}$ , $\quad \ell = 1 \ldots L$

$\mathbf{z}_{\ell}$ = $\text{MLP}(\text{LN}(\mathbf{z}'_{\ell}))$ + $\mathbf{z}'_{\ell}$ , $\quad \ell = 1 \ldots L$

class TransformerEncoderBlock(nn.Sequential):
    def __init__(self,
                 emb_size: int = 768,
                 drop_p: float = 0.,
                 forward_expansion: int = 4,
                 forward_drop_p: float = 0.,
                 **kwargs):
        super().__init__(
            # 第一个残差连接模块：LayerNorm + MultiHeadAttention + Dropout
            ResidualAdd(nn.Sequential(
                nn.LayerNorm(emb_size),
                MultiHeadAttention(emb_size, **kwargs),
                nn.Dropout(drop_p)
            )),
            # 第二个残差连接模块：LayerNorm + FeedForwardBlock + Dropout
            ResidualAdd(nn.Sequential(
                nn.LayerNorm(emb_size),
                FeedForwardBlock(
                    emb_size, expansion=forward_expansion, drop_p=forward_drop_p),
                nn.Dropout(drop_p)
            ))
        )
        
class TransformerEncoder(nn.Sequential):
    def __init__(self, depth: int = 12, **kwargs):
        """
        *[TransformerEncoderBlock(**kwargs) for _ in range(depth)] 是一个列表解析，创建了 depth 个 TransformerEncoderBlock 实例，每个实例都传递了相同的参数 **kwargs。
        * 操作符将列表解析生成的多个 TransformerEncoderBlock 实例解包并传递给 nn.Sequential 的构造函数，从而构建一个包含多个编码器块的序列。
        """
        super().__init__(*[TransformerEncoderBlock(**kwargs) for _ in range(depth)])

整体结构

import torch.nn as nn

class ViT(nn.Sequential):
    def __init__(self,     
                in_channels: int = 3,  # 输入图像的通道数（RGB 图像为 3）
                patch_size: int = 16,  # 补丁的大小（16x16）
                emb_size: int = 768,  # 嵌入维度
                img_size: int = 224,  # 输入图像的大小（224x224）
                depth: int = 12,  # Transformer 编码器的层数
                n_classes: int = 200,  # 类别数，Tiny-ImageNet-200 数据集有 200 个类别
                **kwargs):  # 额外的关键字参数
        super().__init__(
            PatchEmbedding(in_channels, patch_size, emb_size, img_size),  # 图像补丁嵌入层
            TransformerEncoder(depth, emb_size=emb_size, **kwargs),  # Transformer 编码器
            ClassificationHead(emb_size, n_classes)  # 分类头部
        )

# 各组件的详细注释：

# PatchEmbedding:
# 将输入图像分割成固定大小的补丁（patch），并将每个补丁转换为一个高维嵌入向量。
# 输入：形状为 (batch_size, in_channels, img_size, img_size) 的张量。
# 输出：形状为 (batch_size, num_patches + 1, emb_size) 的嵌入向量，其中 +1 是分类标记。

# TransformerEncoder:
# 多层 Transformer 编码器，每层包含一个多头自注意力模块和一个前馈神经网络模块。
# 输入：形状为 (batch_size, num_patches + 1, emb_size) 的嵌入向量。
# 输出：形状为 (batch_size, num_patches + 1, emb_size) 的嵌入向量。

# ClassificationHead:
# 使用分类标记的输出，通过平均池化和全连接层进行最终的分类。
# 输入：形状为 (batch_size, emb_size) 的分类标记嵌入向量。
# 输出：形状为 (batch_size, n_classes) 的类别概率分布。

训练模型

超参数设置

论文中超参数设置
补丁大小 P：选择了 16 和 32 两种不同的补丁大小。
嵌入维度 D：在 192 到 1024 之间选择不同的嵌入维度。
Transformer 层数 L：我们实验了从 12 层到 24 层的不同设置。
注意力头数 h：选择了从 3 到 16 头的注意力机制。

数据处理

使用tinny-imagenet-200数据集，图片大小为64*64，为了适配 Vision Transformer 的输入要求（通常是 224x224），需要对图像进行重新调整和预处理。

数据集结构：

import os

import torchvision.transforms as transforms
import torchvision.datasets as datasets
from torch.utils.data import DataLoader

# 设置数据集路径
data_dir = 'tiny-imagenet-200'
train_dir = os.path.join(data_dir, 'train')
val_dir = os.path.join(data_dir, 'val')

# 定义数据增强和预处理
# transforms.RandomResizedCrop(224)：这个操作会随机裁剪图像的一个子区域，并将其缩放到 224x224 大小。这种裁剪和缩放是随机的，有助于增加训练数据的多样性，从而增强模型的泛化能力。
# transforms.RandomHorizontalFlip()：这个操作会随机水平翻转图像（以 50% 的概率）。这种数据增强方法进一步增加了训练数据的多样性。

transform_train = transforms.Compose([
    transforms.RandomResizedCrop(224),
    transforms.RandomHorizontalFlip(),
    transforms.ToTensor(),
    transforms.Normalize(mean=[0.485, 0.456, 0.406], std=[0.229, 0.224, 0.225])
])

# transforms.Resize(256)：这个操作会将图像的较短边调整到 256 像素，而较长边会按比例缩放。这个步骤确保所有图像的最短边都为 256 像素，从而为后续的中心裁剪做好准备。
# transforms.CenterCrop(224)：这个操作会在图像的中心裁剪出一个 224x224 的区域。这种裁剪方法保证了输入图像的大小一致，有助于模型在验证或测试阶段的稳定性。

transform_val = transforms.Compose([
    transforms.Resize(256),
    transforms.CenterCrop(224),
    transforms.ToTensor(),
    transforms.Normalize(mean=[0.485, 0.456, 0.406], std=[0.229, 0.224, 0.225])
])

# 创建数据集和数据加载器
train_dataset = datasets.ImageFolder(train_dir, transform=transform_train)
val_dataset = datasets.ImageFolder(val_dir, transform=transform_val)

train_loader = DataLoader(train_dataset, batch_size=32, shuffle=True, num_workers=4)
val_loader = DataLoader(val_dataset, batch_size=32, shuffle=False, num_workers=4)

准备工作

import torch.optim as optim

# 设置设备
device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")

# 定义 ViT 模型
model = ViT().to(device)

# 定义损失函数和优化器
criterion = nn.CrossEntropyLoss()
learning_rate = 3e-4
optimizer = optim.Adam(model.parameters(), lr=learning_rate)

训练、验证、预测函数

from tqdm import tqdm
# 训练函数

def train(model, dataloader, criterion, optimizer, device):
    model.train()
    running_loss = 0.0
    correct = 0
    total = 0
    
    for inputs, labels in tqdm(dataloader):
        inputs, labels = inputs.to(device), labels.to(device)
        
        optimizer.zero_grad()
        outputs = model(inputs)
        loss = criterion(outputs, labels)
        loss.backward()
        optimizer.step()
        
        running_loss += loss.item() * inputs.size(0)
        _, predicted = torch.max(outputs, 1)
        total += labels.size(0)
        correct += (predicted == labels).sum().item()
    
    epoch_loss = running_loss / len(dataloader.dataset)
    epoch_acc = correct / total
    
    return epoch_loss, epoch_acc

# 验证函数
def validate(model, dataloader, criterion, device):
    model.eval()
    running_loss = 0.0
    correct = 0
    total = 0
    
    with torch.no_grad():
        for inputs, labels in tqdm(dataloader):
            inputs, labels = inputs.to(device), labels.to(device)
            
            outputs = model(inputs)
            loss = criterion(outputs, labels)
            
            running_loss += loss.item() * inputs.size(0)
            _, predicted = torch.max(outputs, 1)
            total += labels.size(0)
            correct += (predicted == labels).sum().item()
    
    epoch_loss = running_loss / len(dataloader.dataset)
    epoch_acc = correct / total
    
    return epoch_loss, epoch_acc

# 预测函数
def predict(model, dataloader, device):
    model.eval()
    predictions = []
    
    with torch.no_grad():
        for inputs in tqdm(dataloader):
            inputs = inputs.to(device)
            outputs = model(inputs)
            _, predicted = torch.max(outputs, 1)
            predictions.extend(predicted.cpu().numpy())
    
    return predictions

开始训练

# 训练和验证模型
num_epochs = 10
best_acc = 0

for epoch in range(num_epochs):
    print(f"Epoch {epoch+1}/{num_epochs}")
    print("-" * 10)
    
    train_loss, train_acc = train(model, train_loader, criterion, optimizer, device)
    val_loss, val_acc = validate(model, val_loader, criterion, device)
    
    print(f"Train Loss: {train_loss:.4f} Acc: {train_acc:.4f}")
    print(f"Val Loss: {val_loss:.4f} Acc: {val_acc:.4f}")
    
    if val_acc > best_acc:
        best_acc = val_acc
        torch.save(model.state_dict(), 'best_vit_model.pth')
        print("Model saved!")     

print("Training complete!")
# 加载最佳模型进行预测
model.load_state_dict(torch.load('best_vit_model.pth'))

# 创建一个测试数据加载器
test_dir = os.path.join(data_dir, 'test')
test_dataset = datasets.ImageFolder(test_dir, transform=transform_val)
test_loader = DataLoader(test_dataset, batch_size=64, shuffle=False, num_workers=4)

# 进行预测
predictions = predict(model, test_loader, device)

# 打印一些预测结果
print(predictions[:10])

现在手头只有一台四年前的笔记本电脑，训练一个epoch需要一个半小时左右，因为是学习所以只训练一次，学习流程即可。
在这里插入图片描述