SICTF2023 Crypto部分官方WriteWP

SICTF-Crypto官方WriteWP

前言

这次比赛的Crypto部分很新生但是很有意思，重点还是在RSA部分为主（因为树木只会RSA），比较适合新手入门。

Crypto

Ascii

from flag import flag
import base64
flag=str(base64.b32encode(base64.b64encode(flag)))
for i in flag:
    print(chr(ord(i)^3),end='')
#a$HVZDZQ@TJUMGLVHZIYUF1U0NNYDURWWDNM6FFYP1OA[TRPHWJZ7R>>>>$

拿到这道题之后先分析最后的异或，因为异或的自反性质，我们对密文异或3即可拿到base加密后的密文

cipher='a$HVZDZQ@TJUMGLVHZIYUF1U0NNYDURWWDNM6FFYP1OA[TRPHWJZ7R>>>>$'
for i in cipher:
    print(chr(ord(i)^3),end='')
#b'KUYGYRCWIVNDOUKYJZVE2V3MMZGVQTTGMN5EEZS2LBXWQSKTIY4Q===='

但是因为python的base64库只允许传入bytes型数据，所以加密后的密文可能有b’'的冗余，这里用在线网站解一下就好了
![][Ascii1.png]

SICTF{Asc1i_1s_s0_ez!!!}

hashgame

from hashlib import md5
from flag import flag
for i in flag:
    print(md5(str(md5(i.encode("utf-8")).hexdigest()).encode("utf-8")).hexdigest())
'''
999a215b1f8372bb0f1c84c467a1506b
02b0b94ee1fa195ae7959560893f7e3c
297e7ca127d2eef674c119331fe30dff
65c162f7c43612ba1bdf4d0f2912bbc0
ed8a4ab0c0967b14e3bf6b145e153ec9
d24412e1ab190533176a653cef11b185
815e6212def15fe76ed27cec7a393d59
38026ed22fc1a91d92b5d2ef93540f20
cd7fd1517e323f26c6f1b0b6b96e3b3d
a94837b18f8f43f29448b40a6e7386ba
dc0ae7e1387be9b795f5d6299e383759
815e6212def15fe76ed27cec7a393d59
38026ed22fc1a91d92b5d2ef93540f20
dc0ae7e1387be9b795f5d6299e383759
a3655d5c04849a174d341b13d5cf5468
28c8edde3d61a0411511d3b1866f0636
011ecee7d295c066ae68d4396215c3d0
d7afde3e7059cd0a0fe09eec4b0008cd
39abe4bca904bca5a11121955a2996bf
a3655d5c04849a174d341b13d5cf5468
011ecee7d295c066ae68d4396215c3d0
28c8edde3d61a0411511d3b1866f0636
38026ed22fc1a91d92b5d2ef93540f20
dc0ae7e1387be9b795f5d6299e383759
a3655d5c04849a174d341b13d5cf5468
4c0d13d3ad6cc317017872e51d01b238
83be264eb452fcf0a1c322f2c7cbf987
4e44f1ac85cd60e3caa56bfd4afb675e
815e6212def15fe76ed27cec7a393d59
a3655d5c04849a174d341b13d5cf5468
28c8edde3d61a0411511d3b1866f0636
4e44f1ac85cd60e3caa56bfd4afb675e
ed108f6919ebadc8e809f8b86ef40b05
a94837b18f8f43f29448b40a6e7386ba
dcfcd07e645d245babe887e5e2daa016
665f644e43731ff9db3d341da5c827e1
83be264eb452fcf0a1c322f2c7cbf987
39abe4bca904bca5a11121955a2996bf
39abe4bca904bca5a11121955a2996bf
4c0d13d3ad6cc317017872e51d01b238
dc0ae7e1387be9b795f5d6299e383759
011ecee7d295c066ae68d4396215c3d0
5eccf232f5ebb3e780543372692fff18
'''

分析代码发现对flag的每一位进行MD5加密然后对密文再次进行MD5加密，用个在线网站解一下就好了

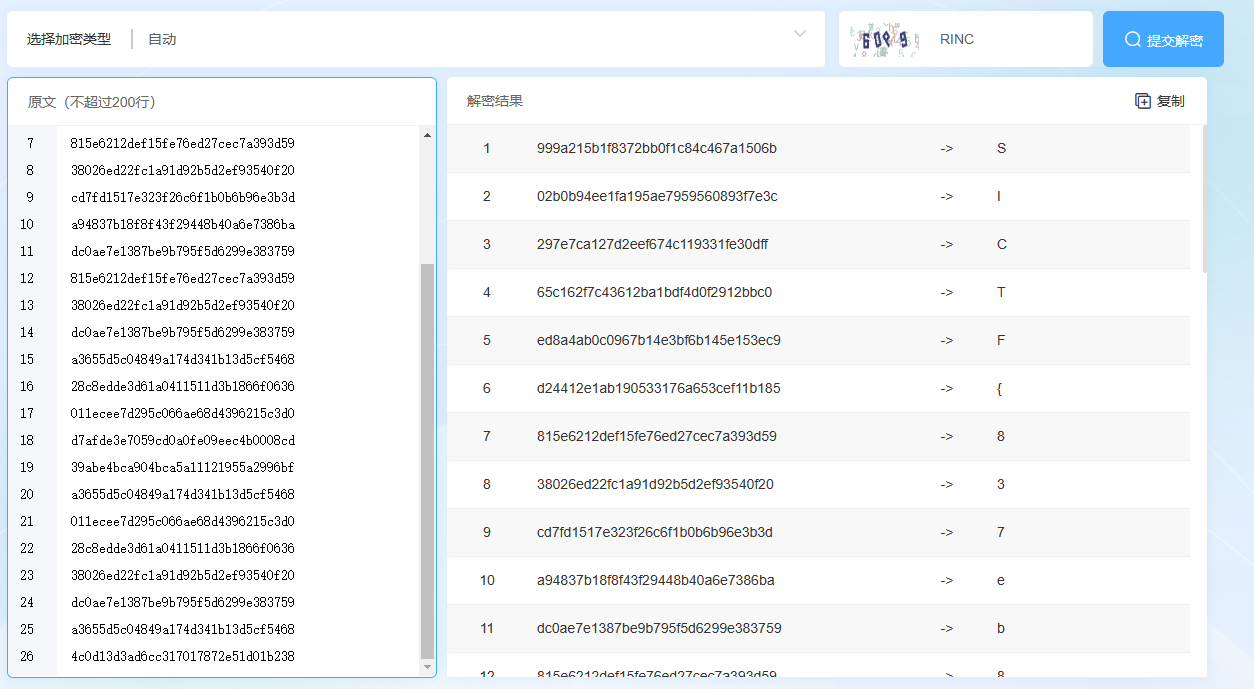
SICTF{837eb83b-14ad-413b-9f58-15ce02fdd9b4} 

baby_rsa

from flag import flag
import libnum
from Crypto.Util.number import getPrime
m=libnum.s2n(flag)
n=getPrime(16)
for i in range(233):
    n*=getPrime(16)
e=65537
c=pow(m,e,n)
print(c)
print(n)
'''
44457399775772165283580795763046604956432217865936749114390645714446263790235445725770165521476841968764175721036280702731933849090719866149354613431301887740671003826556620460836983488011711209908075106260857650574672356032244606425941095128801765463716482316101398637519304864271794460829068714740938719022156283319142938782439784724450045931039355442034325311037568791297455084676548879770834712506552233840348850684727096270392080049993135041218143811167688449496243036317450681348089315258831745988434134987055263393540923865029931594717328162951158311497514418799360413513590684301435386737514918075848373373755748782672860711406169316940293554209702288482064854840802876490202123903888235028119047988176327629542924415737212649237787748145773301112682790682933658516724691338727523894513267588035437093188599375494920656327919129240066252636130803666175859640361767805549884909317548802917210333235914904622641997249853362378711924024129399688535136879208010081166848163897114124726692078532337827810846421365846926064892472698603597461932481745017020417072013702099809833423003201003030492
157077292656328898849823499976497003976795705913326943955927601882559735301000546878663484930436631929909115065166613744548816622146802007640124796249330573411377703969505934904150600987843325674764620305047603408490558134670867673308099650843329640744997672015466571290660161290811275435569339606335117906571999000341133024698424364682800683662193063661214736762852739324479859236963365531207752799197178993887860855078852702337761399225640575281412171035871278933493943575572155382899938265639764715616686123949482372238288859715465115400317136714757882965887595246507450491169518000205087415380208167764110920711042584766805992237919576823121108078407699912757901788925718859790257450499775129521327827653298451904392241906547672843110356658889638496906522290674659574024024440113632175010053065452660076447040937842478007881589334096496073556056726805396937630799201696246079227214272205462258357482722478243481697053301054600954126539848778226175296162997813416634702496577009409960503948474494741296663849482119365434792563324547643352816519125305335959420429699475765642610737903235960423173
'''

观察代码，发现n是由许多的16bit素数相乘得到的，而这些素数很小，是可以被分解出来的

用python手搓个求phi(n)的就行，当然如果懒的话也可以像我一样用sage一键求phi(n)

n = 157077292656328898849823499976497003976795705913326943955927601882559735301000546878663484930436631929909115065166613744548816622146802007640124796249330573411377703969505934904150600987843325674764620305047603408490558134670867673308099650843329640744997672015466571290660161290811275435569339606335117906571999000341133024698424364682800683662193063661214736762852739324479859236963365531207752799197178993887860855078852702337761399225640575281412171035871278933493943575572155382899938265639764715616686123949482372238288859715465115400317136714757882965887595246507450491169518000205087415380208167764110920711042584766805992237919576823121108078407699912757901788925718859790257450499775129521327827653298451904392241906547672843110356658889638496906522290674659574024024440113632175010053065452660076447040937842478007881589334096496073556056726805396937630799201696246079227214272205462258357482722478243481697053301054600954126539848778226175296162997813416634702496577009409960503948474494741296663849482119365434792563324547643352816519125305335959420429699475765642610737903235960423173
c = 44457399775772165283580795763046604956432217865936749114390645714446263790235445725770165521476841968764175721036280702731933849090719866149354613431301887740671003826556620460836983488011711209908075106260857650574672356032244606425941095128801765463716482316101398637519304864271794460829068714740938719022156283319142938782439784724450045931039355442034325311037568791297455084676548879770834712506552233840348850684727096270392080049993135041218143811167688449496243036317450681348089315258831745988434134987055263393540923865029931594717328162951158311497514418799360413513590684301435386737514918075848373373755748782672860711406169316940293554209702288482064854840802876490202123903888235028119047988176327629542924415737212649237787748145773301112682790682933658516724691338727523894513267588035437093188599375494920656327919129240066252636130803666175859640361767805549884909317548802917210333235914904622641997249853362378711924024129399688535136879208010081166848163897114124726692078532337827810846421365846926064892472698603597461932481745017020417072013702099809833423003201003030492
e = 65537
phi = euler_phi(n)
d = gmpy2.invert(e, phi)
m = pow(c,d,n)
print(libnum.n2s(int(m)))

运行即可获得flag

SICTF{13578a78-1bd1-483e-8c01-4d501c8b52bb}

PolyRSA

from Crypto.Util.number import *
from flag import flag
while True:
	k = getRandomNBitInteger(64)
	p = k**5 + 9*k**4 - 20*k**3 + 17*k**5 - 144*k + 47527
	q = k**6 - 8*k**3 + 30*k**3 - 149*k**2 - 14*k + 39293
	if isPrime(p) and isPrime(q):
		break
def encrypt(msg, n, e):
	m = bytes_to_long(msg)
	return pow(m, e, n)
n = p * q
e = 65537
c = encrypt(flag, n, e)
print(f'n = {n}')
print(f'c = {c}')
#n = 2931835714514227696649197851452018066969814603905505893064829694548691616628661422451386639398824072768907608195113790730392677411502544741840786734616614308622423513064577929715025601090611378413475093510051291
#c = 1162375069210804266034094584942794481470301602122091344590668656120128936761168164673823514232328715217241524062023457713973727518007443604233760475552174214966591823835585191443465256735930086309706593996639864

我们观察发现k是随机生成的长度为64bit的数字，而p和q都是由k得到的，整理得到如下关系：

p = k**5 + 9*k**4 - 20*k**3 + 17*k**5 - 144*k + 47527
q = k**6 - 8*k**3 + 30*k**3 - 149*k**2 - 14*k + 39293
n = p * q

将p和q代入n，发现只有k一个未知数了，然后解方程就能得到k，再算p和q就ok了，这里我们用sage解一下方程就能得到k = 10453474106135055672，然后求出p和q进行常规RSA解密

from Crypto.Util.number import long_to_bytes
import gmpy2
n = 2931835714514227696649197851452018066969814603905505893064829694548691616628661422451386639398824072768907608195113790730392677411502544741840786734616614308622423513064577929715025601090611378413475093510051291
c = 1162375069210804266034094584942794481470301602122091344590668656120128936761168164673823514232328715217241524062023457713973727518007443604233760475552174214966591823835585191443465256735930086309706593996639864
k = 10453474106135055672
p = k**5 + 9*k**4 - 20*k**3 + 17*k**5 - 144*k + 47527
q = k**6 - 8*k**3 + 30*k**3 - 149*k**2 - 14*k + 39293
d = gmpy2.invert(65537, (p-1)*(q-1))
print(long_to_bytes(int(pow(c, d, n))))

运行即可获得flag

SICTF{5abeab79-0b03-43c9-a56d-34d92f385080}

RRRSSSAAA

from Crypto.Util.number import *
import gmpy2
import libnum
from secret import flag,hint,alpha

def gen_num(x):
    while True:
        x+=1
        if isPrime(x):
            break
    return x

p = getPrime(512)
q = gen_num(p*alpha)
r = gen_num(q*alpha*2)
s = gen_num(r*alpha*4)
n = p**alpha * q**(alpha