简介
本文简单介绍全向移动运动模型（mecanum和omni）、差分运动模型、四轮滑移转向运动模型和阿克曼运动模型。全向移动机器人与其他机器人相比，其特点是适合工作在工作空间狭小，对机器人的机动性要求高的场合。有源码链接，如读者发现错误及疑问可以下方留言。愿分享共进！
全向移动机器人运动模型分析（mecanum和omni）
全方位运动系统中，Mecanum轮应用最广泛。Mecanum轮(又称瑞典轮)是瑞典Mecanum AB公司工程师Bengt Ilron提出的特殊轮系，其特点为沿轮毂圆周排布着与轮子成一定角度（如45度）且可绕自身轴线进行旋转的辊子。由三个或以上Mecanum 轮按照一定方式排列组成的移动平台具有平面内三个自由度，可同时独立的前后、左右和原地旋转运动，可在不改变自身姿态的情况下向任意方向移动。
其运动学本质是：轮毂外围安装一周与轮毂轴线呈一定角度的无动力辊子作为轮胎，该辊子不仅可绕轮毂轴公转，也能在地面摩擦力作用下绕各自的支撑芯轴自转，两种运动的合成使得接触地面的辊子中心合速度与轮毂轴有一定的夹角，通过调节轮毂速度可改变辊子中心合速度的大小和方向。由同样结构的若干Mecanum 轮按一定规则组成的轮组系统，通过改变各轮毂速度的线性组合，进而控制运动系统中心合速度大小和方向，使机器人实现平面3自由度全方位运动。由于其外观上与斜齿轮相似，麦克纳姆轮也有齿轮啮合时相类似的问题：为了保证运动的平稳性，当前一个辊子与地面即将分离时，后一个辊子必须与地面接触。
图1-1 mecanum及omni全向轮
运动学模型：
如下图所示，坐标系{S}为空间中静止的参考系（map坐标系），坐标系{b}固定在车身上随机器人运动（base_link）。那么机器人在静止参考系中的位置和姿态可以用向量q描述，q=(ϕ,x,y)。在自身参考系{b}中的线速度及角速度为
图1-2 模型图
那么两个参考系之间速度的转换公式如下：
全方位移动机器人必须安装至少3个全向轮，才能实现以任意三维速度q˙=(ϕ˙,x˙,y˙)进行运动。下图为两种典型的全向移动机器人，一种装有3个全向轮，另一种装有4个麦克纳姆轮。
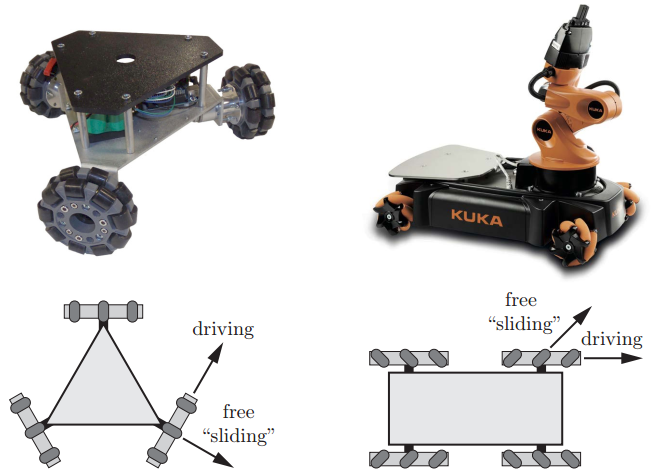
图1-3 实物图及模型图
为了控制全向移动机器人，我们需要知道给每个轮子多大的角速度才能使机器人达到目标速度q˙。为了解答这个问题，我们需要理解单个轮子的运动学，为此建立如下图所示的轮子坐标系：
图1-4 单轮模型
坐标系
建立在轮子中心，根据速度合成定理车轮中心的速度
满足下面的公式：
其中γ为小辊子滚动方向与驱动轮平面的夹角（通常全向轮为0°，麦克纳姆轮为±45°），
是驱动速度，
是自由滑动的速度。解方程(13.3)可以得到
假设轮子半径为r，轮子转动的角速度为u，那么根据上式可得：
为了推导出从小车速度
到轮子i的角速度ui的转换关系，参考最上面的坐标系布置图。轮子坐标系在小车坐标系{b}中的位置和姿态可以用向量(βi,xi,yi)来表达，其中轮子半径为ri，辊子滑动角度为γi。那么从q˙到ui的转换关系如下：
从右到左进行解读：第一个变换矩阵将静止坐标系下的q˙变换为小车局部坐标系{b}中的υb；第二个变换矩阵将小车的局部速度转换为坐标系{b}中的轮子线速度；第三个变换矩阵将坐标系{b}中的轮子线速度转换为轮子坐标系
中的线速度；最后一个变换矩阵将依据公式(13.4)计算轮子角速度。将这几个矩阵合并，可以得到对单个轮子的变换矩阵hi(ϕ)如下：
对于一个全向移动机器人来说，轮子数量m⩾3，矩阵
将静止参考系中的机器人速度
转换为轮子驱动角速度
，将m行hi(ϕ)向量堆叠到一起组成矩阵H(ϕ)，有如下公式：
根据上式我们也可以直接计算出小车局部坐标系下的速度和驱动轮角速度之间的关系，这时转换矩阵将不依赖小车在静止参考坐标系中的朝向角ϕ：
小车上轮子的位置和朝向(βi,xi,yi)，以及辊子夹角γi的选择必须使得矩阵H(0)的秩为3。如果rank(H) < 3，则系统中存在奇异位形，反映在运动学上就是失去部分自由度，即小车不能实现全方位运动。
由于全向轮结构和运动学的特殊性，系统中并不是任一种轮组排列结构形式都可实现全方位运动，多轮构成的系统运动能力和运动控制性能及其驱动性能均与轮组的结构形式密切相关。下面就是两种典型的布局，麦克纳姆轮在小车中的朝向都一致βi=0：
图1-5 机器人模型
根据上面的公式，3个全向轮布置的移动机器人运动学模型为：
（核心公式）
4个麦克纳姆轮布置的移动机器人运动学模型为：
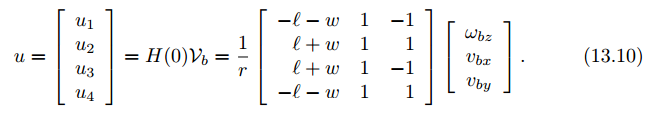（核心公式）
对麦克纳姆轮型移动机器人来说，为向前移动，所有轮子要以相同的速度向前转动；为了侧向移动，1、3轮向前转，2、4轮向后转，转速要相同...
图1-6 mecanum轮运动模型
双轮差分移动机器人运动模型分析
假设WMR（轮式移动机器人）在水平地面上运动，车轮只旋转不打滑，将WMR简化成如图1所示。以WMR的右驱动轮为研究对象,O-XY为WMR工作场地的固定参考坐标系, 
为与WMR固连的坐标系,R为固连坐标系的原点,与右轮轮心重合;
与两驱动轮轴线重合,指向左轮;X和
间的夹角为θ,即WMR的位姿可表示为
;左、右轮的坐标分别为
、
。设L为WMR两驱动轮的轮距; r 为WMR驱动轮的半径; 
分别为WMR左、右驱动轮的角速度。
图2-1 WMR结构简图
两个驱动轮间的约束方程：
左右轮间距L约束为
、
令 α 为WMR的初始姿态,定义其逆时针为正,且 
,则由图 1 可得WMR的姿态角与两驱动轮轮距中点的关系为
根据式(1)和式(2),得
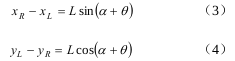
假设 WMR 在任意一初始位置 AB,经时间 t转过 θ 角后到达另一位置 A ′ B ′ ,如图 2 所示,则左驱动轮比右驱动轮多转过的曲线位移为
即:
图2-2 WMR运动位姿变化
由于 WMR 的运动方式只有直线运动和圆弧运动两种,若作为基点的驱动轮(文中为右驱动轮)的角速度 ω R = ω = c 已知,则左驱动轮的角速度 
根据式(6)得
若 θ = 0 ,即对于直线运动而言,显然
两驱动轮同速,即直线运动是曲线运动的特例。
WMR运动学方程：
当 WMR 驱动轮的角速度已知,由式(3)、(4)和(6)并根据图 2-2,可得到 WMR 的运动学模型
（核心公式）
如果 WMR 按照确定的轨迹运动,即, 
已知时,则驱动轮的运动规律就可根据下式求出
阿克曼机器人运动模型分析
阿克曼约束模型：
阿克曼模型满足四轮车辆转向过程中，车辆处于纯滚动无滑动。如图3-1所示，为了实现转向时转向车轮是纯滚动，不发生横向滑移，四个车轮绕同一个ICR转动，并且内外轮转角之间满足（1）：
根据几何关系解的：
式 (1)、(2) 中, α 1 、 α 2 分别表示内、外轮的转向角, α 表示前轮轴中点虚拟轮转向角;b 为二分之一轮距; l 为轴距。据式 (2),可用 α表示机器人的真实转向角。在运动模型中,定义所有的角度都是逆时针为正,顺时针为负。
图3-1 基于阿克曼原理的机器人运动模型
阿克曼机器人的运动模型：
对模型的假设：(1) 将整个机器人视为刚体,车轮视为刚性轮；(2) 假设机器人处于二维平面上运动,不考虑俯仰和侧倾带来的影响;(3) 只考虑前进与转向的运动行为。
基于上述假设,为了便于表述机器人在平面中的位置,建立全局坐标系 
和机器人基坐标系 
,选择后轮轴中点作为基坐标系的原点,如图 3-1 所示坐标系。根据几何关系可得
由此可得角速度 ω 与转向角 α 之间的关系式为：
（核心公式）
在全局坐标系下,机器人的位置由基坐标系原点的坐标 (x(t),y(t)) 确定。全局坐标系与局基坐标系之间的角度差为 θ t ,表示机器人在 t 时刻的航向角。
差动驱动的滑移转向运动模型分析：
如图4-1所示，移动机器人速度和机器人位置显示，展示了履带式滑动转向机器人在某一时刻的
运动状态。
图4-1 移动机器人速度和机器人位置显示
整体平移速度v在（1）中定义，旋转w在（2）中定义，其中L是轮子或轨道之间的距离并且等于2b。每个轨道或车轮的速度变换在（3）和（4）中计算。
如果平移速度为零且旋转大于零，我们可以从（3）和（4）中提取右轮的速度等于左轮的负速度，反之亦然。如果旋转速度为零并且平移速度大于零，那么左右速度是相同的。左右机器人轨道由PID速度控制器控制。因此我们可以考虑左右轨道的实际速度也由公式（3）和（4）给出。左右轨道直接干扰环境（地面）。轨道和地面之间发生滑动。滑倒是非常不可取的，但它是必要的防滑 -转向的移动 机器人。在[ 19 ]中讨论了由于移动机器人的轨道 - 土壤相互作用引起的轨道滑移的复杂动态。灾难现场的地面非常难以预测，因此我们不依赖于车轮编码器提供的测距仪。差动驱动移动机器人的运动学的紧凑形式可以通过[ 17 ]中的等式（5）建模，其中
和
在的方向的速度X和Y在机器人基架。
差动驱动机器人实际上是沿圆形路径描述运动，如图4-2所示，当实现（v，w）的速度控制时。
图4-2 基于平移和旋转速度形成的圆周运动
圆周运动有其旋转中心（CR）。当旋转速度接近零或零时，考虑直线运动。圆形运动半径R与每个轨道上的速度之间的关系在（6）中定义。
如果旋转速度为零（vr = vl），那么在极限情况下，圆形路径退化为一条线; 它是一个半径无限的圆。因此，线和圆可以被认为是移动 机器人原始运动。通用路径 跟随器算法包括低级别的冲突检查。这可确保机器人不会与环境中的动态障碍物或墙壁发生碰撞。碰撞检查器也可以包含在系统中。
参考文献
[1]冬木远景.全向移动机器人与V-rep中全向移动机器人仿真 https://www.cnblogs.com/21207-iHome/p/7911748.html
[2]王仲民,阎兵.双轮差速驱动式移动机器人运动规划[J].中国知网
[3]徐保来,管贻生,苏泽荣,谷世超,黄 晶.改进动态窗口法的阿克曼移动机器人局部路径规划器 [J].工业自动化
[4]任孝平 , 蔡自兴.基于阿克曼原理的车式移动机器人运动学建模[J].智能系统学报
[5]Wheeled Mobile Robotics From Fundamentals Towards Autonomous System (参看CHAPTER 2 Motion Modeling for Mobile Robots)
[6]Tianmiao Wang, Yao Wu *, Jianhong Liang, Chenhao Han, Jiao Chen and Qiteng Zhao.Analysis and Experimental Kinematics of a Skid-Steering Wheeled Robot Based on a Laser Scanner Sensor[J].Sensors 2015, 15, 9681-9702; doi:10.3390/s150509681
[7]奋斗的小鸟lcy.机器人滑动转向驱动方式(Skid-steer Drive) https://blog.youkuaiyun.com/github_30605157/article/details/52170006
[8]Peter Lepej 1 *, Johannes Maurer 2 , Suzana Uran 1 and Gerald Steinbauer 1.Dynamic Arc Fitting Path Follower for Skid-steered Mobile Robots[J]. 2016 IEEE International Conference on Robotics and Automation (ICRA)
源代码
扫一扫
2950
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
