球队“食物链“ JAVA版

JAVA版球队食物链算法

原创已于 2022-03-25 17:41:08 修改 · 719 阅读

1 ·

CC 4.0 BY-SA版权

文章标签：

#java #算法

于 2022-03-25 17:40:29 首次发布

java 专栏收录该内容

6 篇文章

订阅专栏

本文介绍了一个JAVA实现的算法，通过深度优先搜索（DFS）加剪枝策略来解决球队之间的胜负关系问题，旨在找出一个闭合的食物链，即一个队能够连续战胜其他队伍并最终战胜最初挑战的队伍。

球队“食物链" JAVA版

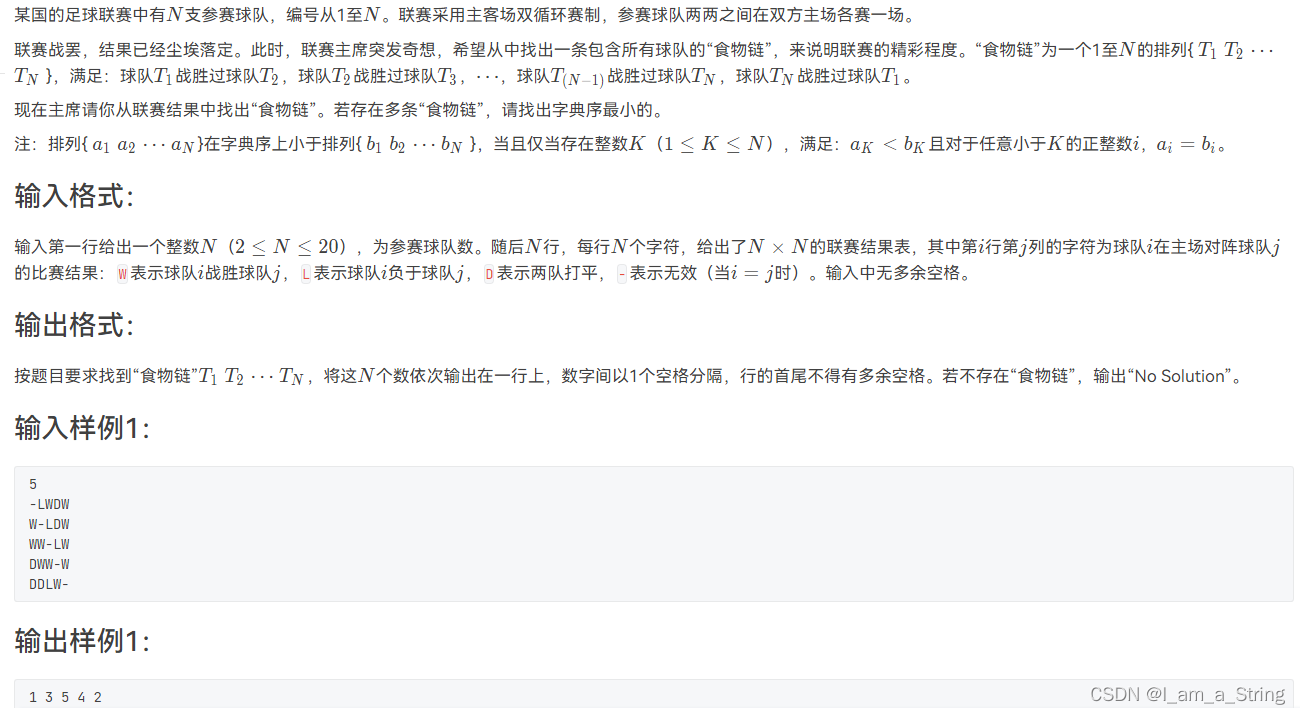
dfs+剪枝，向下一层探索前判断是否还存在战胜T1的队伍即可


import java.util.Scanner;

public class Main {
	static String reuslt;
	static int N;
	static int flag=0;
	static int[][] map = new int[21][21];
	static int[] visited = new int[21];
	public static void main(String[] args) {
		Scanner in = new Scanner(System.in);
		String tmp;
		N=in.nextInt();
		in.nextLine();
		for(int i=1;i<=N;i++) {
			tmp = in.nextLine();
			for(int j=1;j<=N;j++) {
				if(tmp.charAt(j-1)=='W')map[i][j]=1;
				if(tmp.charAt(j-1)=='L')map[j][i]=1;
			}
		}
		for(int i=1;i<=N;i++) {
			if(flag==1) break;
			visited[i]=1;
			dfs(i,i,1,i+"");
			visited[i]=0;
		}
		if(flag==1) System.out.println(reuslt);
		else System.out.println("No Solution");
		
	}
	
	private static void dfs(int first, int now, int cnt, String tmp) {
		if(flag==1)return;
		if(cnt==N) {
			if(map[now][first]==1) {
				flag=1;
				reuslt=tmp;
			}
			return;
		}
		boolean f = false;
		for(int i=1;i<=N;i++) {
			if((visited[i]==0&&map[i][first]==1)||map[now][first]==1) {
				f=true;
				break;
			}
		}
		if(!f)return;
		
		for(int i=1;i<=N;i++) {
			if(map[now][i]==1&&visited[i]==0) {
				visited[i]=1;
				dfs(first, i, cnt+1, tmp+" "+String.valueOf(i));
				visited[i]=0;
			}
		}
		
	}

}