逻辑回归

一、损失函数的求解

逻辑回归是一个简单的二分类算法，分类边界可以是线性的也可以是非线性的。

通俗的解释就是，对于给定的样例X，我们要求出一组theta，将theta与X 相乘的结果作为Sigmoid函数的输入，这样就能得到一个概率值

逻辑回归算法的损失函数如何确定？

               由于逻辑回归是一个二分类算法，所以在给定的数据集的标签中只有两个类别，分别是0和1。

当真实的数据集y=1时 ，通过Sigmoid函数得出的结果值p越小，损失越大，同理， 当真实的数据集y=0时，通过Sigmoid函数得出的结果值p越大 ，损失越大。     

所以在逻辑回归中我们定义如下的损失函数：

当真实的数据集y=1时 ，根据图像可知，p越小，cost越大

当真实的数据集y=0时 ，根据图像可知，p越大，cost越大

            通过整理我们得到只有一个样本的损失函数为：

            当数据集为m个样本时的损失函数为：

 

上式就是逻辑回归中的损失函数

 

二、损失函数梯度的求解

1、对逻辑回归的损失函数的的每一个求导，其求导公式的表达形式如下图所示：

 

2、首先对sigmoid函数求导

3、对log sigmoid函数进行求导

                                                     

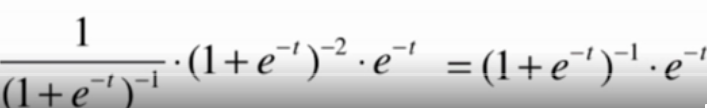
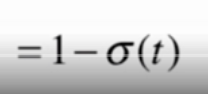
4、对损失函数的前半部分进行求导

5、对log(1-sigmoid)函数求导

 

6、对损失函数的后半部分求导

7、将前后两部分的导数相加

8、最后得到损失函数对其中的某一个求导的梯度为：

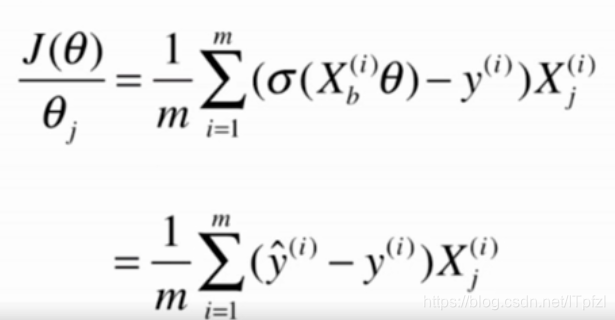
9、求出损失函数的梯度后再进行向量化