数据结构与算法-递归思想

递归&分治&回溯

递归不仅仅是一种编程代码的习惯方式，而更多的是一种分析业务逻辑的思维方式.有很多人在说到递归的时候，往往就是觉得递归不就是函数里面嵌套相同函数吗?就像下面这样

    void fun(int a){
        fun(a);
    }

但是，很多同学在写一个递归的时候，是只知道能解决一个问题，但是不知道写递归还要注意内在几个重要性，下面我们就来说明这些个特性。注意，写递归一定要看重这种编程思想，而不是只局限于递归函数的写法

一:分治
分治就是在分析一个问题的时候，可以把它拆成n个小的问题，例如食堂打饭排队，我想知道我当前的位置是第几个,但是我又不能从头开始数（一数就被别人插队了）,所以我就问前面一个人他是第几位，我只要知道前面一个人的位置，我就知道了自己的位置了吧。那前面一个人不知道自己的位置那么再问钱一个人，一直到问道第一个。这样我们就把获取自己排队位置的问题分解为n个相同问题。这就是递归的分治思想
二：回溯
在将一个问题分解成小问题的时候,每个小问题一定要有确定的返回答案，比如上面排队问题,最终的返回答案肯定就是问到第一个人的时候，第一个人确定知道自己是第一个了吧。如果问题没有返回答案，那么这个递归就会无线循环下去。我们知道在 函数调用函数中，会占用栈内存的，无限递归会导致栈溢出的异常 StackOverflowError
比如下面的递归

```java

    public static int intMore(int a){
        int c = a+a;
        intMore(intMore(c));
        return c;
    }```


所以我们在写递归的时候，一定要在首先在代码开始的地方加上回溯的条件
    public static int intMore(int a){
        //回溯条件
        if (a > 1000){
            return a;
        }
        int c = a+a;
        intMore(intMore(c));
        return c;
    }

那么 考虑到分治和回溯 就可以写好递归的了吗？答案是 Of course not ！！！下面我们就以著名的** 斐波那契队列** 来说明(ps:面试的时候常考哟)

我们知道，斐波那契数列 就是 从数列的第三项开始 ,每一项都等于前两项之和
0、1、1、2、3、5、8、13、21、34
那么在数学上的公式就是
F(0) = 0 ,F(1) = 1 , F(n) = f(n-1) + F(n-2) (n >= 2 ),那么我们就用代码来实现这个数列

一：直接套用

    /**
     * 斐波那契队列
     * @return
     */

    static  long count = 0; //函数调用次数
    
    public static int fibonacci_1(int n){
        count ++;
        if (n <=2 ){
            if (n == 0){
                return 0;
            }else {
                return 1;
            }
        }
        return fibonacci_1(n-1) + fibonacci_1(n-2);
    }

这段代码，既有分治也有回溯,而且跟公式基本吻合吧，那么我们来测试一下代码性能
测试代码

        for (int i = 0;i< 56;++i){

            long time = System.currentTimeMillis();
            int res = fibonacci_1(i);
            System.out.println(" i = "+ i +" res = "+ res +"  ,运算次数count = " + count +" ,time ="   +(System.currentTimeMillis() - time));
        }

i = 0 res = 0 ,运算次数count = 1 ,time =0
i = 1 res = 1 ,运算次数count = 2 ,time =0
i = 2 res = 1 ,运算次数count = 3 ,time =0
i = 3 res = 2 ,运算次数count = 6 ,time =0
i = 4 res = 3 ,运算次数count = 11 ,time =0
i = 5 res = 5 ,运算次数count = 20 ,time =0
i = 6 res = 8 ,运算次数count = 35 ,time =0
i = 7 res = 13 ,运算次数count = 60 ,time =0
i = 8 res = 21 ,运算次数count = 101 ,time =0
i = 9 res = 34 ,运算次数count = 168 ,time =0
i = 10 res = 55 ,运算次数count = 277 ,time =0
i = 11 res = 89 ,运算次数count = 454 ,time =0
i = 12 res = 144 ,运算次数count = 741 ,time =0
i = 13 res = 233 ,运算次数count = 1206 ,time =0
i = 14 res = 377 ,运算次数count = 1959 ,time =0
i = 15 res = 610 ,运算次数count = 3178 ,time =0
i = 16 res = 987 ,运算次数count = 5151 ,time =0
i = 17 res = 1597 ,运算次数count = 8344 ,time =0
i = 18 res = 2584 ,运算次数count = 13511 ,time =0
i = 19 res = 4181 ,运算次数count = 21872 ,time =0
i = 20 res = 6765 ,运算次数count = 35401 ,time =0
i = 21 res = 10946 ,运算次数count = 57292 ,time =0
i = 22 res = 17711 ,运算次数count = 92713 ,time =1
i = 23 res = 28657 ,运算次数count = 150026 ,time =0
i = 24 res = 46368 ,运算次数count = 242761 ,time =1
i = 25 res = 75025 ,运算次数count = 392810 ,time =0
i = 26 res = 121393 ,运算次数count = 635595 ,time =1
i = 27 res = 196418 ,运算次数count = 1028430 ,time =0
i = 28 res = 317811 ,运算次数count = 1664051 ,time =1
i = 29 res = 514229 ,运算次数count = 2692508 ,time =3
i = 30 res = 832040 ,运算次数count = 4356587 ,time =4
i = 31 res = 1346269 ,运算次数count = 7049124 ,time =5
i = 32 res = 2178309 ,运算次数count = 11405741 ,time =14
i = 33 res = 3524578 ,运算次数count = 18454896 ,time =18
i = 34 res = 5702887 ,运算次数count = 29860669 ,time =28
i = 35 res = 9227465 ,运算次数count = 48315598 ,time =43
i = 36 res = 14930352 ,运算次数count = 78176301 ,time =71
i = 37 res = 24157817 ,运算次数count = 126491934 ,time =151
i = 38 res = 39088169 ,运算次数count = 204668271 ,time =182
i = 39 res = 63245986 ,运算次数count = 331160242 ,time =321
i = 40 res = 102334155 ,运算次数count = 535828551 ,time =464
i = 41 res = 165580141 ,运算次数count = 866988832 ,time =1028
i = 42 res = 267914296 ,运算次数count = 1402817423 ,time =1160
i = 43 res = 433494437 ,运算次数count = 2269806296 ,time =1871
i = 44 res = 701408733 ,运算次数count = 3672623761 ,time =2893
i = 45 res = 1134903170 ,运算次数count = 5942430100 ,time =4737
i = 46 res = 1836311903 ,运算次数count = 9615053905 ,time =7420

当运行到 第i = 46 时，就需要七秒多了，而且 函数的调用次数 为 9615053905 ，一个超大值,那么这肯定不能在生产项目上这么干的吧，为啥会这样的
我们来画图来分析 函数调用 ，当i = 6的时候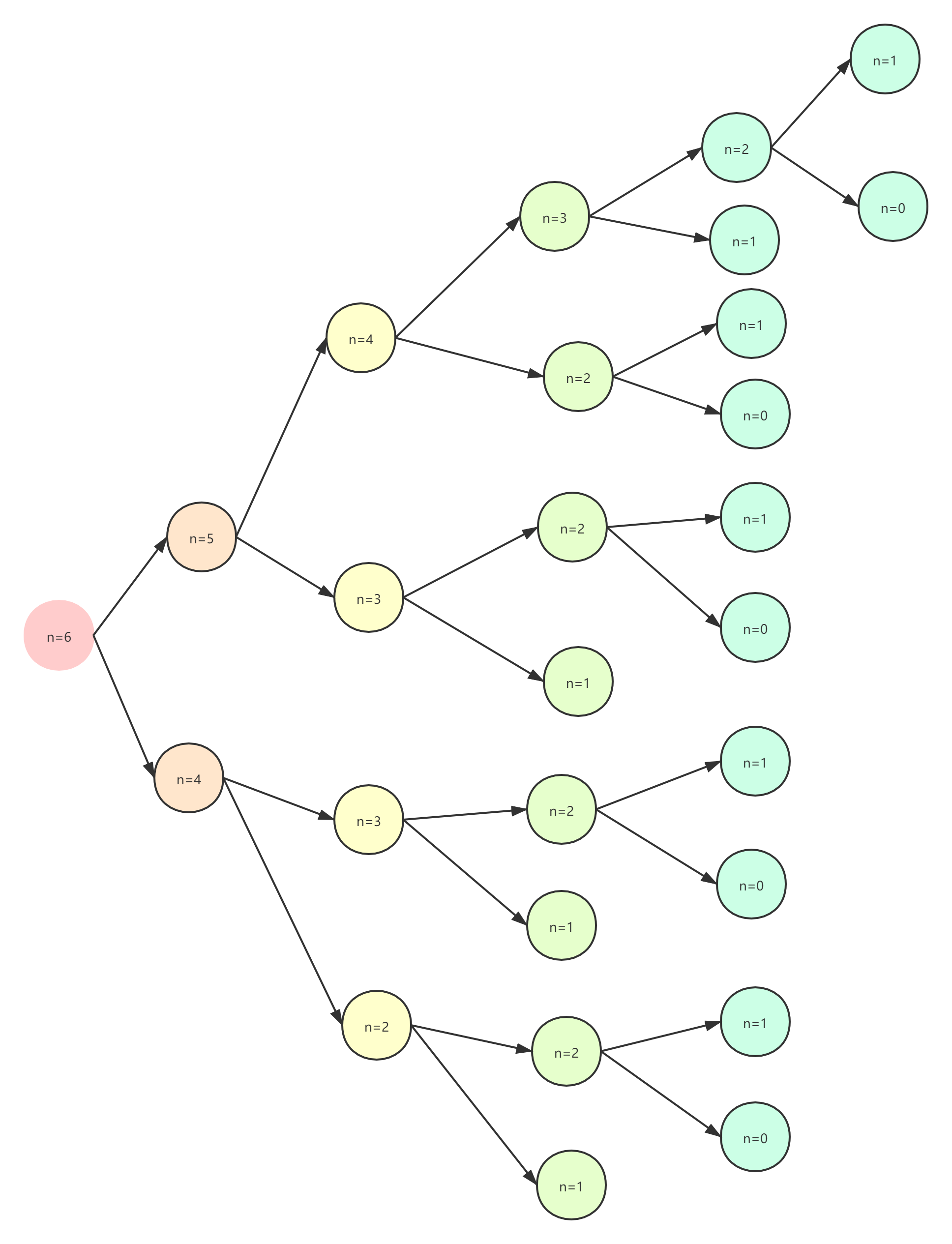
我们发现，每进入下一个节点就会调用一倍的次数,会重复调用很多相同的节点,时间复杂度为 O(2^n),我们知道在优化函数时间复杂度的时候就是将 时间复杂度尽可能优化到 O(1) 或者O（n）;具体请看
时间复杂度
，上面代码出的问题是因为重复调用，那为啥会重复调用呢？那其实各个分支之间不知道其他的分支已经计算除了结果，其实就是每个分支都自己计算出一次结果，但是我们只需要函数计算一次结果就可以了。那么怎么解决呢？答案就是 我们把计算结果带进去不就可以了吗
那么下面给出两种方法解决这个问题.

第一种:如果你对递归没有把握的话，那么我们就要记住，大部分(我们说的是大部分)递归都可以用循环来解决的，我们只要存储计算出来的值就可以了，给出代码

    static  long count = 0; //函数调用次数

    public static  int fibonacci_2(int n){
        count ++;
        if (n <=1 ){
            if (n == 0){
                return 0;
            }else {
                return 1;
            }
        }
        int a = 0;
        int b = 1;
        int c =0;
        for (int i = 2;i<= n;++i){
            c =a+b;
            a = b;
            b = c;
        }
        return c;
    }

再用相同的代码检测结果
i = 0 res = 0 ,运算次数count = 1 ,time =0
i = 1 res = 1 ,运算次数count = 2 ,time =0
i = 2 res = 1 ,运算次数count = 3 ,time =0
i = 3 res = 2 ,运算次数count = 4 ,time =0
i = 4 res = 3 ,运算次数count = 5 ,time =0
i = 5 res = 5 ,运算次数count = 6 ,time =0
i = 6 res = 8 ,运算次数count = 7 ,time =0
i = 7 res = 13 ,运算次数count = 8 ,time =0
i = 8 res = 21 ,运算次数count = 9 ,time =0
i = 9 res = 34 ,运算次数count = 10 ,time =0
i = 10 res = 55 ,运算次数count = 11 ,time =0
i = 11 res = 89 ,运算次数count = 12 ,time =0
i = 12 res = 144 ,运算次数count = 13 ,time =0
i = 13 res = 233 ,运算次数count = 14 ,time =0
i = 14 res = 377 ,运算次数count = 15 ,time =0
i = 15 res = 610 ,运算次数count = 16 ,time =0
i = 16 res = 987 ,运算次数count = 17 ,time =0
i = 17 res = 1597 ,运算次数count = 18 ,time =0
i = 18 res = 2584 ,运算次数count = 19 ,time =0
i = 19 res = 4181 ,运算次数count = 20 ,time =0
i = 20 res = 6765 ,运算次数count = 21 ,time =0
i = 21 res = 10946 ,运算次数count = 22 ,time =0
i = 22 res = 17711 ,运算次数count = 23 ,time =0
i = 23 res = 28657 ,运算次数count = 24 ,time =0
i = 24 res = 46368 ,运算次数count = 25 ,time =0
i = 25 res = 75025 ,运算次数count = 26 ,time =0
i = 26 res = 121393 ,运算次数count = 27 ,time =0
i = 27 res = 196418 ,运算次数count = 28 ,time =0
i = 28 res = 317811 ,运算次数count = 29 ,time =0
i = 29 res = 514229 ,运算次数count = 30 ,time =0
i = 30 res = 832040 ,运算次数count = 31 ,time =0
i = 31 res = 1346269 ,运算次数count = 32 ,time =0
i = 32 res = 2178309 ,运算次数count = 33 ,time =0
i = 33 res = 3524578 ,运算次数count = 34 ,time =0
i = 34 res = 5702887 ,运算次数count = 35 ,time =0
i = 35 res = 9227465 ,运算次数count = 36 ,time =0
i = 36 res = 14930352 ,运算次数count = 37 ,time =0
i = 37 res = 24157817 ,运算次数count = 38 ,time =0
i = 38 res = 39088169 ,运算次数count = 39 ,time =0
i = 39 res = 63245986 ,运算次数count = 40 ,time =0
i = 40 res = 102334155 ,运算次数count = 41 ,time =1
i = 41 res = 165580141 ,运算次数count = 42 ,time =0
i = 42 res = 267914296 ,运算次数count = 43 ,time =0
i = 43 res = 433494437 ,运算次数count = 44 ,time =0
i = 44 res = 701408733 ,运算次数count = 45 ,time =0
i = 45 res = 1134903170 ,运算次数count = 46 ,time =0
i = 46 res = 1836311903 ,运算次数count = 47 ,time =0
i = 47 res = -1323752223 ,运算次数count = 48 ,time =0
i = 48 res = 512559680 ,运算次数count = 49 ,time =0
i = 49 res = -811192543 ,运算次数count = 50 ,time =0
i = 50 res = -298632863 ,运算次数count = 51 ,time =0
i = 51 res = -1109825406 ,运算次数count = 52 ,time =0
i = 52 res = -1408458269 ,运算次数count = 53 ,time =0

可以看出，计算时间基本都是 0，非常之快啊，这里的时间复杂度就是O（n）;

第二种：上面说大部分递归都可以用循环解决，那么小部分呢？实在用循环解决不了的，那么也有解决方法，就是 尾递归,所谓尾递归,就是在递归的时候把结果带进去，然后每次递归都能返回值（抛弃了 回溯 ），我们给出代码

    /**
     * 斐波那契队列 尾递归方法
     * @param n
     * @param pre 上一次计算的的
     * @param res 这一次计算的值
     * @return
     */

    static  long count = 0; //函数调用次数
    public static  int fibonacci_3(int n,int pre,int res){
        count ++;
        if (n <=2 ){
            return  res;
        }
        //将 结果res 带入参数,必定有返回值
        return fibonacci_3(n-1,res,pre +res);
    }

我们再测试一下

i = 1 res = 1 ,运算次数count = 1 ,time =0
i = 2 res = 1 ,运算次数count = 2 ,time =0
i = 3 res = 2 ,运算次数count = 4 ,time =0
i = 4 res = 3 ,运算次数count = 7 ,time =0
i = 5 res = 5 ,运算次数count = 11 ,time =0
i = 6 res = 8 ,运算次数count = 16 ,time =0
i = 7 res = 13 ,运算次数count = 22 ,time =0
i = 8 res = 21 ,运算次数count = 29 ,time =0
i = 9 res = 34 ,运算次数count = 37 ,time =0
i = 10 res = 55 ,运算次数count = 46 ,time =0
i = 11 res = 89 ,运算次数count = 56 ,time =0
i = 12 res = 144 ,运算次数count = 67 ,time =0
i = 13 res = 233 ,运算次数count = 79 ,time =0
i = 14 res = 377 ,运算次数count = 92 ,time =0
i = 15 res = 610 ,运算次数count = 106 ,time =0
i = 16 res = 987 ,运算次数count = 121 ,time =0
i = 17 res = 1597 ,运算次数count = 137 ,time =0
i = 18 res = 2584 ,运算次数count = 154 ,time =0
i = 19 res = 4181 ,运算次数count = 172 ,time =0
i = 20 res = 6765 ,运算次数count = 191 ,time =0
i = 21 res = 10946 ,运算次数count = 211 ,time =0
i = 22 res = 17711 ,运算次数count = 232 ,time =0
i = 23 res = 28657 ,运算次数count = 254 ,time =0
i = 24 res = 46368 ,运算次数count = 277 ,time =0
i = 25 res = 75025 ,运算次数count = 301 ,time =0
i = 26 res = 121393 ,运算次数count = 326 ,time =0
i = 27 res = 196418 ,运算次数count = 352 ,time =0
i = 28 res = 317811 ,运算次数count = 379 ,time =0
i = 29 res = 514229 ,运算次数count = 407 ,time =0
i = 30 res = 832040 ,运算次数count = 436 ,time =0
i = 31 res = 1346269 ,运算次数count = 466 ,time =0
i = 32 res = 2178309 ,运算次数count = 497 ,time =0
i = 33 res = 3524578 ,运算次数count = 529 ,time =0
i = 34 res = 5702887 ,运算次数count = 562 ,time =0
i = 35 res = 9227465 ,运算次数count = 596 ,time =0
i = 36 res = 14930352 ,运算次数count = 631 ,time =0
i = 37 res = 24157817 ,运算次数count = 667 ,time =0
i = 38 res = 39088169 ,运算次数count = 704 ,time =0
i = 39 res = 63245986 ,运算次数count = 742 ,time =0
i = 40 res = 102334155 ,运算次数count = 781 ,time =0
i = 41 res = 165580141 ,运算次数count = 821 ,time =0
i = 42 res = 267914296 ,运算次数count = 862 ,time =0
i = 43 res = 433494437 ,运算次数count = 904 ,time =0
i = 44 res = 701408733 ,运算次数count = 947 ,time =0
i = 45 res = 1134903170 ,运算次数count = 991 ,time =0
i = 46 res = 1836311903 ,运算次数count = 1036 ,time =0
i = 47 res = -1323752223 ,运算次数count = 1082 ,time =0
i = 48 res = 512559680 ,运算次数count = 1129 ,time =0
i = 49 res = -811192543 ,运算次数count = 1177 ,time =0
i = 50 res = -298632863 ,运算次数count = 1226 ,time =0
i = 51 res = -1109825406 ,运算次数count = 1276 ,time =0
i = 52 res = -1408458269 ,运算次数count = 1327 ,time =0
i = 53 res = 1776683621 ,运算次数count = 1379 ,time =0
i = 54 res = 368225352 ,运算次数count = 1432 ,time =0
i = 55 res = 2144908973 ,运算次数count = 1486 ,time =0
这里时间还是0，函数调用次数相比之前的也没那么高了,因为这里时间复杂度就是O（n）啊；
尾递归的思想就是，每次调用都必须返回确定的值，将返回的值当作参数传给下一次调用,类似从后开始往前算,就不用回溯了

多多关注,欢迎提出意见!!!