梯度下降算法

 梯度下降法(gradient descent)是一个最优化算法，常用于机器学习和人工智能当中用来递归性地逼近最小偏差模型。

         梯度下降的损失函数是通过迭代法一步步求解，得到最优解。

1.假设函数

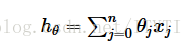
2.代价函数的公式

3. 损失函数的可视化图

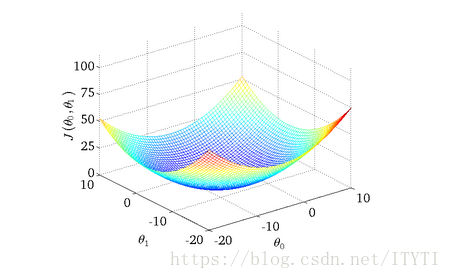
4.批量梯度下降公式（BGD）

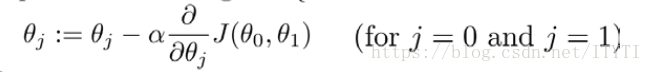
    其中a为学习率

如果a太大，那么梯度下降算法可能汇越过最低点，甚至可能无法收敛

如果a太小，每次移动很小步，这样需要很多步才能到达最低点

5.多变量梯度下降

 其中x0=1

下图为单变量和多变量的对比

6.梯度下降法实践——特征尺度

 在我们解决多为特征问题的时候，我们要保证这些特征都具有相近的尺度，这将帮助梯度下降算法更快的收敛。

方法是：

          1.尽量将所有的特征缩放到-1到1之间（理想情况）

          2.归一化

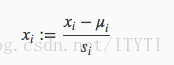
             其中u为平均值，S为标准差（即最大值-最小值）

 7.正规方程解向量

      经数学证明使用线性代数也可以直接求解特征向量，使得 代价函数J()最小

  8.梯度下降与正规方程的比较

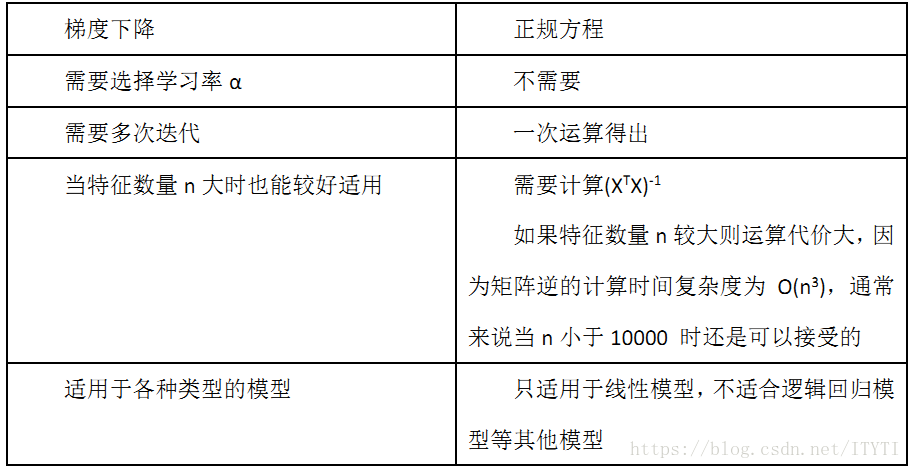
总的来说，只要特征变量的数目并不大，具体的特征数量小于一万，正规方程是一种很好的方法；而特征数量比较大推荐使用梯度下降。