算法设计与分析: 3-18 收集样本问题

3-18 收集样本问题

---

问题描述

机器人 Rob 在一个有 n*n 个方格的方形区域 F 中收集样本。(i,j)方格中样本的价值 为 v(i,j)，如下图所示。

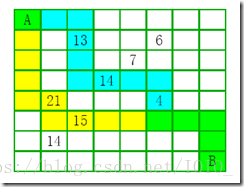
Rob 从方形区域 F 的左上角 A 点出发，向下或向右行走，直到右下角的 B 点，在走过的 路上，收集方格中的样本。Rob 从 A 点到 B 点共走 2 次，试找出 Rob 的 2 条行走路径，使其取得的样本总价值最大。

给定方形区域 F 中的样本分布，编程计算 Rob 的 2 条行走路径，使其取得的样本总价值最 大。

数据输入：
第 1 行有 1 个正整数 n，表示方形区域 F 有 n*n 个方格。 接下来每行有 3 个整数，前 2 个表示方格位置，第 3 个数为该位置样本价值。最后一行是 3 个 0。

---

Java

import java.util.Scanner;

//沿着从A到B的对角线方向进行扫描，每次从左下到右上连线上最多取2个样本值
public class ShouJiYangBen {
    private static int n;//n X n个方格
    private static int[][][][] h;//h[x1][y1][x2][y2]: 到达(x1,y1)和(x2,y2)处取得的最大价值
    private static int[][] g;//g[i][j]: 方格(i,j)处样本的价值

    public static void main(String[] args){
        Scanner input = new Scanner(System.in);

        while (true){
            n = input.nextInt();
            h = new int[2*n][2*n][2*n][2*n];
            g = new int[2*n][2*n];

            while (true){
                int x,y,v;
                x = input.nextInt();
                y = input.nextInt();
                v = input.nextInt();
                if(x==0 && y==0 && v==0)
                    break;
                g[x][y] = v;
            }
//            g[1][1] = 0;
//            g[n][n] = 0;
            dynamic();

            System.out.println(h[n][n][n][n]);
        }


    }

    private static void dynamic(){
        int x1,y1,x2,y2,s,v;
        for(int i=0; i<=n; i++)
            for(int j=0; j<=n; j++)
                for(int k=0; k<=n; k++)
                    for(int m=0; m<=n; m++)
                        h[i][j][k][m] = 0;

        h[1][1][1][1] = g[1][1];

        for(s=2; s<=n+n-1; s++){
            for(x1=1; x1<=s-1; x1++)
                for(x2=1; x2<=s-1; x2++){
                    y1 = s - x1;
                    y2 = s - x2;
                    v = h[x1][y1][x2][y2];
                    val(x1+1,y1,x2+1,y2,v);
                    val(x1+1,y1,x2,y2+1,v);
                    val(x1,y1+1,x2+1,y2,v);
                    val(x1,y1+1,x2,y2+1,v);
                }
        }
    }

    private static void val(int x1, int y1, int x2, int y2, int v){
        if(x1==x2 && y1==y2)
            h[x1][y1][x2][y2] = max(h[x1][y1][x2][y2], v+g[x1][y1]);//递推关系
        else
            h[x1][y1][x2][y2] = max(h[x1][y1][x2][y2], v+g[x1][y1]+g[x2][y2]);//递推关系
    }

    private static int max(int a, int b){
        return a > b ? a : b;
    }
}

---

Input & Output

8
2 3 13
2 6 6
3 5 7
4 4 14
5 2 21
5 6 4
6 3 15
7 2 14
0 0 0
67

---

Reference

王晓东《计算机算法设计与分析》（第3版）P95