差分

最新推荐文章于 2022-07-24 18:34:01 发布

原创最新推荐文章于 2022-07-24 18:34:01 发布 · 165 阅读

0 ·

CC 4.0 BY-SA版权

算法笔记专栏收录该内容

52 篇文章

订阅专栏

本文详细介绍了差分算法在一维和二维数组中的应用，通过更新差分数组实现对原数组区间加法操作。在一维情况下，通过增加和减少差分数组元素实现区间加法；在二维矩阵中，通过四个操作更新差分数组，以达到对子矩阵加法的效果。同时提供了C++代码示例，展示了如何进行操作并恢复原数组。

差分算法

一维差分

首先我们定义a是原数组，b是差分数组

b数组的含义表示为
$\cdots+b[i]$
核心操作是在a数组的某个区间(L~R)上加上c
$c\\ b[R + 1] -= c$

那么根据定义：

a数组是b数组的前缀和，在b[L]的地方加上了c，对前面的数都不会有影响，但是后面所有的a数组都等价于全部加上了c，而我们为了保证只在区间内影响，就可以同样根据b数组前缀和的定义，在b[R + 1]的地方减去c就实现了上述的结果

#include <iostream>

using namespace std;

int n, m;

int a[100000 + 10];
int b[100000 + 10];

int main(){
    cin >> n >> m;
    for(int i = 1; i <= n; i++){
        cin >> a[i];
        b[i] += a[i];
        b[i + 1] -= a[i]; //更新数组，同样根据操作定义
    }
    
    while(m--){
        int l, r, c;
        cin >> l >> r >> c;
        b[l] += c;
        b[r + 1] -= c;
    }
    for(int i = 1; i <= n; i++) a[i] = a[i - 1] + b[i];
    
    for(int i = 1; i <= n; i++) cout << a[i] << " ";
    
    return 0;
}

二维差分

给定原矩阵a[i, j]，构造b[i, j]，使得a是b的二维前缀和

**核心操作：**给以(x1,y1)，为左上角，(x2,y2)为右下角的子矩阵中的所有数加上c

如何操作呢，其实就可以顺便好好考虑一下上面的一维差分和二维前缀和就很好理解了

操作方法就是
$\begin{array}{lcl} b[x1][y1] += c \\ b[x1][y2 + 1] -= c \\ b[x2 + 1][y1] -= c \\ b[x2 + 1][y2 + 1] +=c \end{array}$

简易操作证明：

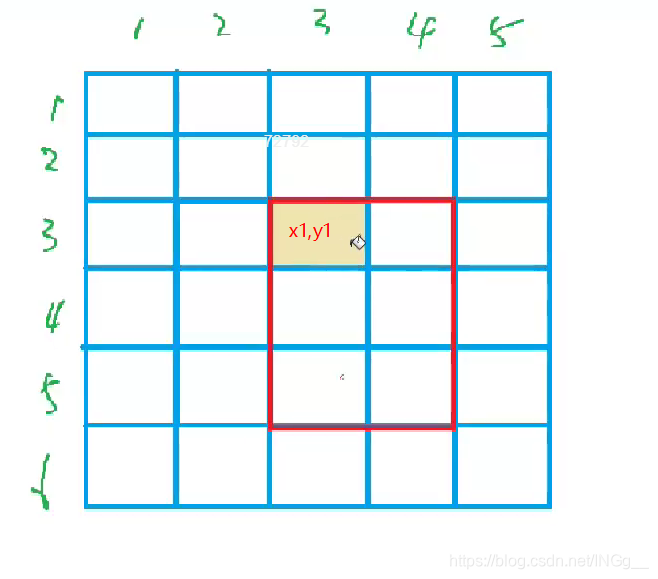
在这里插入图片描述

对这个点进行操作之后，包含这个点的所有的前缀和都会加上c，而他所影响的就是这个点所有右下角的点即：

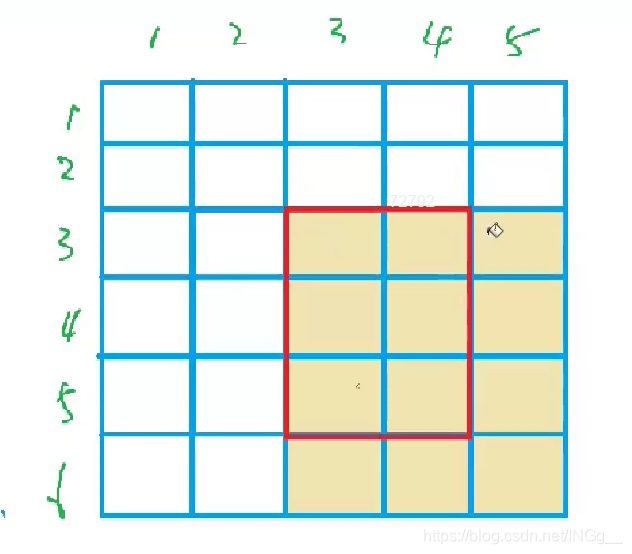
在这里插入图片描述

而进行了b[x1][y2 + 1] -= c操作后，这个点右下角的点就不会受影响了，即：

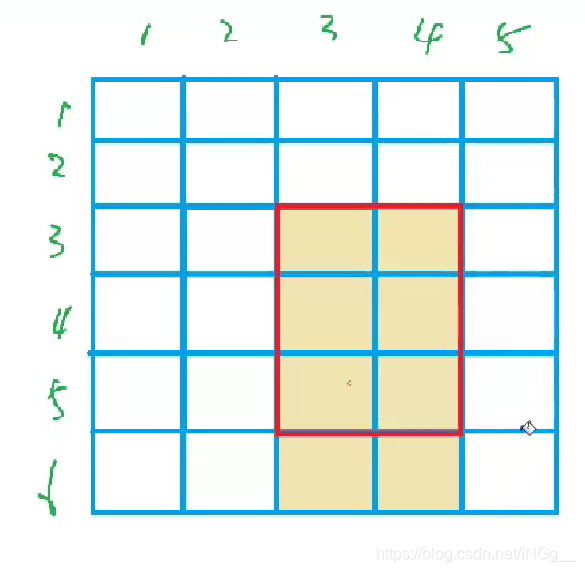
在这里插入图片描述

同理，下一步：

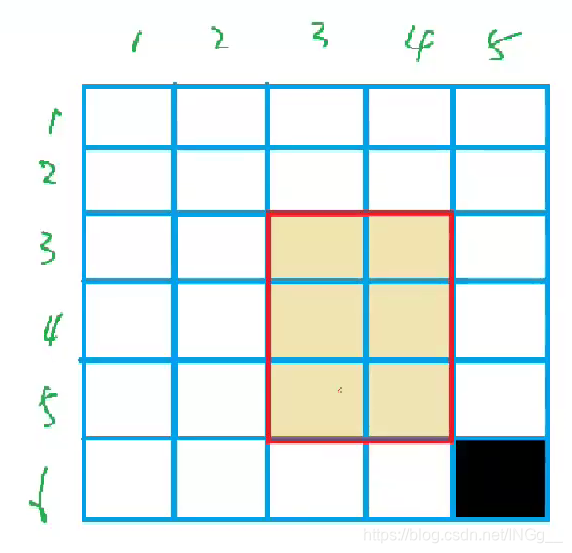
在这里插入图片描述

而最右下角的那个多减了一次c，所以加回来就好了

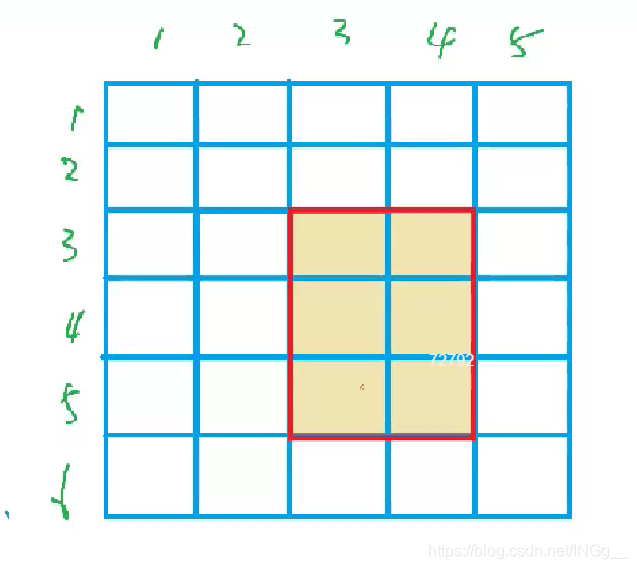
在这里插入图片描述

证毕

#include <iostream>

using namespace std;

const int N = 1000 + 10;

int a[N][N];
int b[N][N];

int n, m, q;

void insert(int x1, int y1, int x2, int y2, int c){ // 写成函数形式方便操作
    b[x1][y1] += c;
    b[x1][y2 + 1] -= c;
    b[x2 + 1][y1] -= c;
    b[x2 + 1][y2 + 1] += c;
}

int main(){
    cin >> n >> m >> q;
    for(int i = 1; i <= n; i++){
        for(int j = 1; j <= m; j++){
            scanf("%d",a[i] + j);
            insert(i, j, i, j, a[i][j]); //根据操作就能构造好了差分数组
        }
    }
    
    while(q--){
        int x1,y1,x2,y2,c;
        cin >> x1 >> y1 >> x2 >> y2 >> c;
        insert(x1, y1, x2, y2, c);
    }
    
    for(int i = 1; i <= n; i++){  // 根据二维前缀和的定义来对原数组进行复原，注意这里不是二维前缀和的操作，而是以某点为右下角的前缀和数组的构造
        for(int j = 1; j <= m; j++){
            a[i][j] = a[i - 1][j] + a[i][j - 1] - a[i - 1][j - 1] + b[i][j];
        }
    }
    
    for(int i = 1; i <= n; i++){
        for(int j = 1; j <= m; j++){
            printf("%d ", a[i][j]);
        }
        printf("\n");
    }
    return 0;
}

图片来源：https://www.acwing.com/video/686/