动态规划（一）

最新推荐文章于 2024-12-13 00:24:16 发布

INGNIGHT

最新推荐文章于 2024-12-13 00:24:16 发布

阅读量169

点赞数

CC 4.0 BY-SA版权

分类专栏： leetcode

本文链接：https://blog.youkuaiyun.com/INGNIGHT/article/details/99637540

leetcode 专栏收录该内容

510 篇文章

订阅专栏

本文深入探讨了斐波纳契数列、爬楼梯问题、三角形路径和最小路径和等经典动态规划问题的解决策略。通过递归、记忆化搜索和动态规划三种方法对比，详细分析了每种方法的时间和空间复杂度，展示了如何通过优化减少重复计算，提高算法效率。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

一.斐波纳挈数列

1.1递归

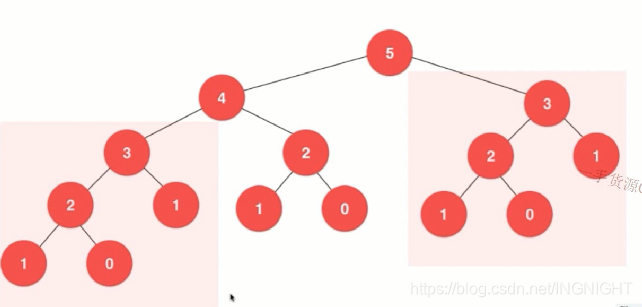
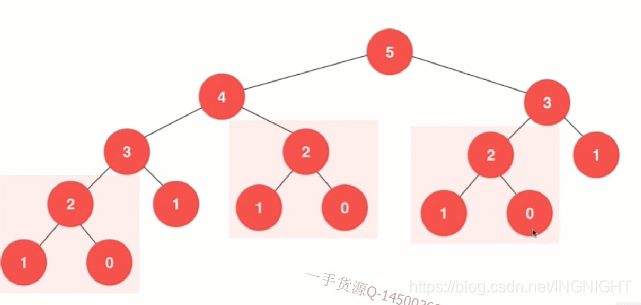
斐波纳挈递归解法时间复杂度O(2^n)，测试方法可以计算10,20,40.看计算时间

从图中可以看出获得我们的递归树，存在大量重复计算

#include <iostream>

using namespace std;

int num = 0;

int fib(int n) {
    ++num;
    if(n == 0)
        return 0;
    if(n == 1)
        return 1;
    return fib(n-1) + fib(n-2);
}

int main() {
    num = 0;
    clock_t timeStart = clock();
    cout << fib(10) << endl;
    clock_t timeEnd = clock();
    cout << "num: " << num << " time: " << timeEnd - timeStart << endl;

    num = 0;
    timeStart = clock();
    cout << fib(20) << endl;
    timeEnd = clock();
    cout << "num: " << num << " time: " << timeEnd - timeStart << endl;

    num = 0;
    timeStart = clock();
    cout << fib(40) << endl;
    timeEnd = clock();
    cout << "num: " << num << " time: " << timeEnd - timeStart << endl;

    return 0;
}

1.2记忆化搜索

使用数组将重复计算的过程记录下来，下次再遇到这个值不在使用递归计算的方式来计算这个值，而是直接取记录的值return回去

#include <iostream>
#include <vector>

using namespace std;

vector<int> memo;
int num = 0;

// 记忆化搜索
int fib(int n) {
    ++num;
    if(n == 0)
        return 0;
    if(n == 1)
        return 1;
    if(memo[n] == -1) {
        memo[n] = fib(n-1) + fib(n-2);
    }
    return memo[n];
}

int main() {
    memo.resize(41, -1);
    num = 0;
    clock_t timeStart = clock();
    cout << fib(10) << endl;
    clock_t timeEnd = clock();
    cout << "num: " << num << " time: " << timeEnd - timeStart << endl;

    num = 0;
    timeStart = clock();
    cout << fib(20) << endl;
    timeEnd = clock();
    cout << "num: " << num << " time: " << timeEnd - timeStart << endl;

    num = 0;
    timeStart = clock();
    cout << fib(40) << endl;
    timeEnd = clock();
    cout << "num: " << num << " time: " << timeEnd - timeStart << endl;

    return 0;
}

1.3动态规划

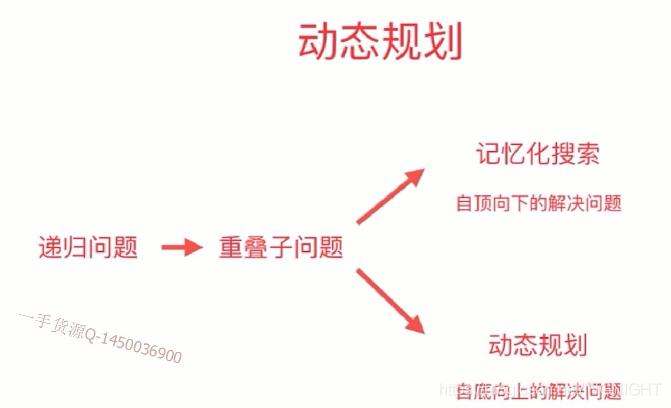
动态规划：将原问题拆解成若干个子问题，同时保存子问题的答案，使得每个子问题只求解一次，最终获得原问题的答案（重复计算）

没有递归调用，调用函数有额外时间开销，空间来讲，使用递归调用占用系统栈空间，使用记忆化的调用次数是2n-1次

二、climbing stairs

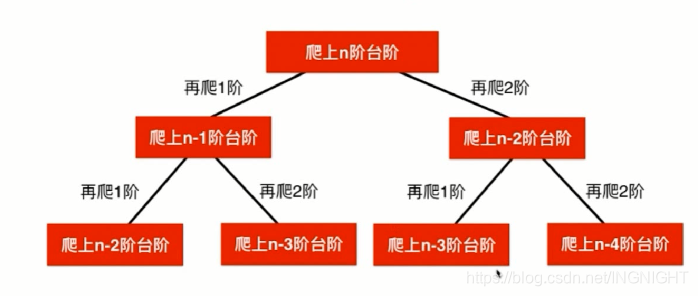
到达楼梯顶端的方法:可以由到达倒数第一节楼梯的方法,加上,可以到达倒数第二节楼梯的方法的总和

class Solution {    
    private:    
    int calcWays(int n) {           
        if(n == 1)                               
            return 1;                             
        if(n==2)                                 
            return 2;                                    
        return calcWays(n-1) + calcWays(n-2);            
    }                                                    
    public:                                              
        int climbStairs(int n) {                         
            return calcWays(n);                          
        }                                                
};

记忆化搜索

class Solution {    
    vector<int> memo;
    private:    
    int calcWays(int n) {           
        if(n == 0 || n == 1)                     
            return 1;                             
        if(memo[n] == -1)
            memo[n] = calcWays(n-1) + calcWays(n-2);     
        return memo[n];
    }                                                    
    public:                                              
        int climbStairs(int n) {                         
            memo = vector<int>(n+1, -1);
            return calcWays(n);                          
        }                                                
};

时间复杂度:O(N)
a.DP状态的定义
f(n):到第n阶的总走法个数
b.DP方程

public int climbStairs(int n) {
    if (n == 0 || n == 1 || n == 2) {
        return n;
    }
    int[] mem = new int[n];
    mem[0] = 1;
    mem[1] = 2;
    for (int i = 2; i < n; ++i) {
        mem[i] = mem[i-1] + mem[i-2];
    }
    return mem[n-1];
}

public int climbStairs(int n) {
    if (n <= 2) return n;
    int one_step_before = 2;
    int two_steps_before = 1;
    int all_ways = 0;
    
    for (int i = 2; i < n; ++i) {
        all_ways = one_step_before + two_step_before;
        two_steps_before = one_step_before;
        one_step_before = all_ways;
    }
    return all_ways;
}

def climbStairs(self, n):
    """
    :type n: int
    :rtype: int
    """
    x, y = 1,1
    for _ in range(1,n):
        x,y = y, x+y
    return y

三.Triangle

[1].状态定义:DP[i,j]:从底bottom走到i,j这个点,路径和最小值
bottom->(i,j)
path sum,min
[2].方程:
DP[i,j]=min(DP(i+1, j), DP(i+1, j+1)) + Triangle[i,j]
DP[m-1, j] = Triangle[m-1, j]
DP[0, 0]为所求结果
时间复杂度O(m*n)
空间复杂度

class Solution {                                                                                    
public:                                                                                             
    int minimumTotal(vector<vector<int> >& triangle) {                                              
        vector<int> mini = triangle[triangle.size()-1];                                             
        for (int i = triangle.size() - 2; i >= 0; --i) {                                            
            for (int j = 0; j < triangle[i].size(); ++j) {                                          
                mini[j] = triangle[i][j] + min(mini[j], mini[j+1]);                                 
            }                                                                                       
        }                                                                                           
        return mini[0];                                                                             
    }                                                                                               
};

四、Minimum Path Sum

参考：https://blog.youkuaiyun.com/program_developer/article/details/83757712

class Solution {                                                                                    
public:                                                                                             
    int minPathSum(vector<vector<int>>& grid) {                                                     
        int row = grid.size();                                                                      
        if (row <= 0) {                                                                             
            return 0;                                                                               
        }                                                                                           
        int col = grid[0].size();                                                                   
        vector<vector<int> > min_path_sum(row, vector<int>(col));                                   
        min_path_sum[row-1][col-1] = grid[row-1][col-1];                                            
        for (int i = row-2; i >= 0; --i) {                                                          
            min_path_sum[i][col-1] = min_path_sum[i+1][col-1] + grid[i][col-1];                     
        }                                                                                           
        for (int i = col-2; i >= 0; --i) {                                                          
            min_path_sum[row-1][i] = min_path_sum[row-1][i+1] + grid[row-1][i];                     
        }                                                                                           
        for (int i = row-2; i >= 0; --i) {                                                          
            for (int j = col-2; j >= 0; --j) {                                                      
                min_path_sum[i][j] = min(min_path_sum[i+1][j], min_path_sum[i][j+1]) + grid[i][j]; 
            }                                                                                       
        }                                                                                           
        return min_path_sum[0][0];                                                                  
    }                                                                                               
};